トポロジカル極性表面積は計算コストの低い推定PSA

化合物の性質を表す指標として様々な「記述子」が開発されてきたことを「RDKitにおける記述子の扱い方をリピンスキーの法則を通して学ぶ」という記事で説明しました．今回とりあげる極性表面積（PSA）も，分子記述子の１つになります．

この記事ではPSAの定義と計算法から，トロポジカルPSAというPSAを低コスト計算で推定したものを紹介します．PSAとTPSAはほとんど同じものとして扱われがちですが，その歴史的背景や特徴を知っておくことで，実際に運用していく際に役立つ場面があると思います．

トポロジカル極性表面積のオリジナル文献は次の論文になります．参考にしてください．「Fast Calculation of Molecular Polar Surface Area as a Sum of Fragment-Based Contributions and Its Application to the Prediction of Drug Transport Properties」J. Med. Chem. 2000, 43, 3714.

極性表面積（PSA）とは
1. PSAの特徴
2. PSA計算における問題点
トポロジカル極性表面積
終わりに

極性表面積（PSA）とは

化合物の極性表面積（Polar Surface Area; PSA）とは分子表面のうち極性を帯びている部位の面積値の総和になります．極性を帯びている部位は，通常酸素や窒素などのへテロ元素周辺ですから，これらの部分構造を足し合わせたものと考えてよいです．

PSAの特徴

PSAはオクタノール/水分配比率（logP）などと同様に，分子の極性・脂溶性を示す記述子になります．PSAと膜透過性に関する実験データとの間にはよい相関があることが判明しています．例えばあまりに大きなPSA（140 Å²以上）を有する化合物は膜透過性が低いことが経験的に知られています．

PSA計算における問題点

これまで述べてきたようにPSAは化合物の膜透過性などを評価する上で有用な指標であることが明らかとなっていました．しかし実際にPSAを計算で求めようとすると，以下に示すようにいくつかの問題が存在することが知られていました．

分子のコンフォメーション

定義からわかりますように，PSAの算出には分子の立体構造が必要になります．分子は1つのコンフォメーションを取っているとは限りませんから，フレキシブルな分子ではいくつかのコンフォメーションに対してPSAを求める必要があるかもしれません．

前者の1つの立体配座のみを考慮したPSAを，single-conformer PSA（単一配座PSA），後者の分子が取り得る複数の配座をボルツマン分布で考慮したPSAをdynamic PSA（ダイナミックPSA）と区別して呼ぶこともあります．

分子表面の計算

ある立体構造・コンフォメーションに対して分子表面を求めることが，PSAの計算には必要となります．その分子表面も，ファンデルワールス表面を用いる場合もあれば，コノリー表面（Connolly surface）を用いる場合もあり，統一性に欠けていました．

へテロ元素の定義

さらに肝心の極性を帯びている部位を構成する「へテロ元素」の定義すらも研究者によって異なりました．ある人は酸素と窒素のみを考慮していたのに対し，別の人はリンや硫黄もへテロ元素としてPSAを計算していました．

PSA計算値の特徴

このようにPSAの計算に際しては，立体構造や分子表面の計算コストが大きいことに加えて，いくつかの一貫性に欠ける問題が知られていました．

しかし，それぞれの方法で求めたPSAの値自体は膜透過性とよい相関を示すことがわかっていました．つまり，コンフォマーを複数考慮してもしなくても，どの分子表面を用いても，そしてどの元素をへテロ元素として考慮しても，全体の傾向としては問題がないということがわかりました．

この事実は，より簡便なPSAの推定法の開発の余地を示すものでした．計算コストを低く抑えつつ，精度よくPSAを求めるという課題を解決するために考案されたのがトポロジカル極性表面積（TPSA）です．

トポロジカル極性表面積

TPSAでは分子の３次元構造を考えずに分子内の原子の結合パターン（トポロジー）のみからPSAを推定します．これがトポロジカル極性表面積という名前の由来になります．

PSAは極性部位の表面積の「総和」ということと，PSAとTPSAがしばしば同じものであるかのように記述されていることから，TPSAの「T」がTotal（合計）であると間違えている方がいらっしゃいます．正しくは「トポロジカル」ですので，正しく理解しておきましょう

TPSAの特徴

TPSAは前述のPSA計算における問題点を克服するために，結合パターンに注目し，各部位のPSAにおける寄与を足し合わせることによってPSAの推定を行います．

結合パターンのみを考えることで計算コストの大幅な低減
へテロ元素として酸素・窒素・リン・硫黄を考慮することで計算手法の統一
大規模な医薬品様な化合物データベースを用いたパラメータ化による精度向上

といった特徴があげられます．特に計算速度は2から3桁のオーダーでの向上が達成されています．

TPSAの算出方法

World Drug Index収載の化合物に対して単一立体配座を考慮したPSAを計算しました．また酸素・窒素・リン・硫黄を含む部分構造を43個選択し，計算したPSAに対する最小二乗法によって各部分構造の重みをパラメータ化しました．

このように，ある指標を部分構造からの寄与の総和として扱う方法はケモインフォマティクスで頻出する考え方になります．また部分構造へと分解することで原子ごとの寄与を可視化することも容易になります．たとえば下の図はタキソールのTPSAへの原子ごとの寄与を可視化したものになります．

RDKitを用いてこのように原子ごとの寄与を可視化する方法は「RDKitの類似度マップを用いて原子ごとの寄与を可視化する」という記事で解説しています．参照してみてください．

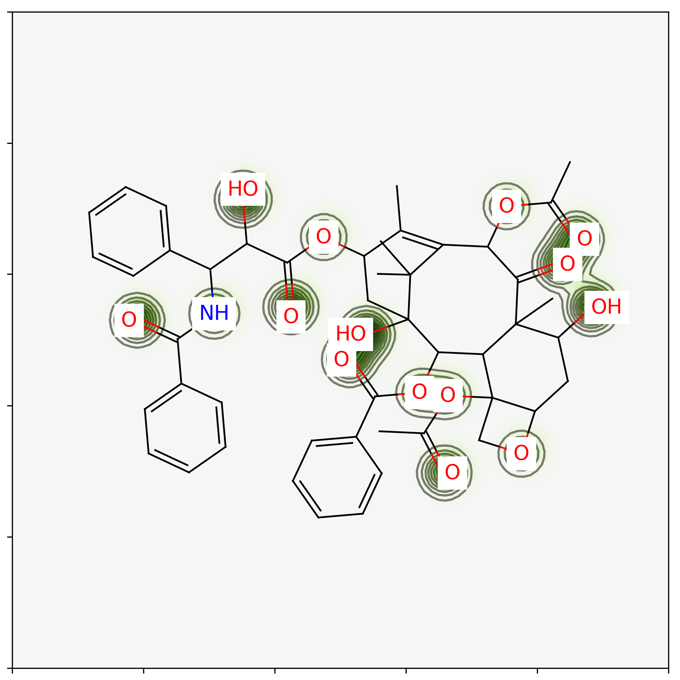
どうやってPTSAを得るか

計算コストが低く，汎用されている記述子になりますので様々なソフトで計算が可能です．ここではChemDrawとRDKitについて計算方法を示します．

ChemDraw

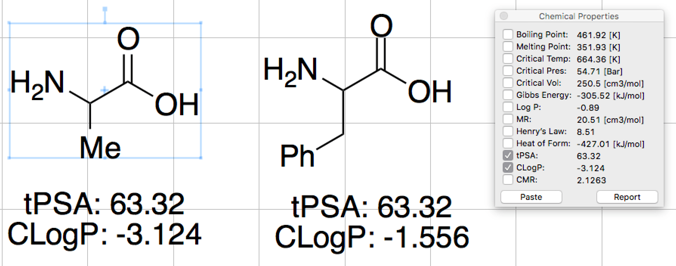
合成化学者にお馴染みのChemDrawでは「Chemical Properties Window」から得ることができます．

RDKit

Chem.Descriptorsモジュール

python用のケモインフォマティクス用ライブラリであるRDKitでは，TPSAをはじめとした各種記述子の計算はDescriptorsモジュールに実装されています．

下のコードでは，

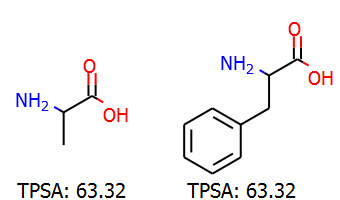
アラニンとフェニルアラニンを含むChemDrawファイルから作成したSDFを読み込み
TPSAを計算
凡例として構造式と一緒に表示

を行っています．上のChemDrawの場合と同じ値になっていることがわかります．

# ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import Draw, Descriptors
from rdkit.Chem.Draw import rdMolDraw2D
from IPython.display import SVG
print(rdBase.rdkitVersion) # 2017.03.3

# 分子の用意
suppl = Chem.SDMolSupplier('./chemdraw_tpsa.sdf')
mols = [x for x in suppl if x is not None]
len(mols) # 2

# TPSAの計算
declist = Descriptors.descList
calc = {}
for (i,j) in declist:
    calc[i] = j
tpsa = [calc['TPSA'](i) for i in mols]

# 描画
view = rdMolDraw2D.MolDraw2DSVG(340,200,170,200)
option = view.drawOptions()
option.legendFontSize=20
option.padding=0.1
view.DrawMolecules(mols, legends=['TPSA: '+str(x) for x in tpsa])
view.FinishDrawing()
svg = view.GetDrawingText()
SVG(svg.replace('svg:', ''))
with open('rdkit_tpsa.svg', 'w') as f:
    f.write(svg)

RDKitを用いた２次元構造の描画については「RDKitでの構造式描画を詳しく解説」という記事で解説しています．参照してみてください．