化合物の脂溶性は溶解性をはじめ,吸収・代謝などの薬物動態にも大きな影響を与える要素です.化合物の脂溶性を表す記述子はこれまでにいくつか知られていますが,最も用いられているものはオクタノール/水分配係数,logPです.
LogPのPは分子の有機層(オクタノール層)と水層中の平衡状態での濃度比率で,その常用対数を取ったものがLogPになります.大きい数字は有機層における濃度が高いことを示しますので,脂溶性が高いことを意味します.
個々の化合物について実験的にLogPの値を求めることもできますが,時間・コストの面からあまり現実的ではなく,報告されている化合物数もあまり多くありません.また当然ですがまだ合成されていない化合物のLogP値は実験的には得られません.そのためケモインフォマティクスの研究者達はさまざまなアプローチを用いてLogPを推定しようとしてきました.
なおあるpHにおける濃度比率を示す値はLogDpHと呼びます.イオン状態を適切に記述する必要があるため,一般にLogPよりも予測が難しい値です.
この記事ではLogP推定に用いられる代表的なアプローチとアルゴリズムについて簡単に紹介していきます.その過程でタイトルの通り,ChemDrawで計算可能な「CLogP」も数あるLogP計算方法の1つに過ぎないということを説明します.
LogP推定の代表的なアプローチ
現在用いられているLogP推定のアプローチは大きく分けて,
- 部分構造を中心としたアプローチ
- 化合物の特徴を中心としたアプローチ
に分けられます.両者ともにさらにいくつかのカテゴリーへと分けることができます.
部分構造を基にしたアプローチ
分子の部分構造に着目した場合,
- 分子をいくつかのフラグメントに分けたアプローチ
- 分子を個々の原子にまで分けたアプローチ
の2つが考えられます.
初期の方法
最初の報告されたLogPを推定する方法は,実験的に知られたLogP値をもとにして,置換基効果を考えることで新規化合物のLogPを推定しようというものでした.
特に芳香環上の置換基をHからXに変えた際の置換基効果πを
$$ \pi_{X} = \log P_{X} – \log P_{H} $$
のように定義しました.このπと親化合物のLogPを用いて未知のLogPを推定するわけです.
この手法は同じような化合物クラスについては一定の成果を上げましたが,例えばベンゼン誘導体で得られたπはピリジン誘導体には適用できないといった欠点を抱えていました.
フラグメントに着目したアプローチ
この方法では分子をある一定のルールに従ってフラグメント化し,
- あらかじめ決定した寄与率に基づいて,フラグメントごとにLogPへの寄与を計算
- フラグメント化にともない失われた分子内相互作用などに対する補正値を計算
という2つの要素を考慮します.数式化すると以下のようになります.
$$ \log P = \sum_{i=1}^{N} a_{i}f_{i} + \sum_{j=1}^{M} b_{j}f_{j} $$
1原子以上の部分構造をフラグメントとして用いることで
- 利点:フラグメント内の電子的相互作用をうまく記述できる
- 欠点:恣意的なフラグメント化や,計算に加味されない重要な部分構造が存在しうる
といった利点・欠点が生じます.
CLogP
フラグメントを用いる方法で最も広く使われているものがLeoとHanschによって1993年に発表された「CLogP」プログラムになります.その後も初期には定義されていなかったフラグメントを追加することで精度を向上させた新しいバージョンが発表されています.
CLogPでは正確に測定されたLogPデータが手に入る比較的小さな分子の構造をフラグメントとして用いてパラメーター化を行っています.
フラグメント化の特徴としてはヘテロ原子に複数結合していない炭素を「独立炭素」として定義します.フラグメント化によって独立炭素と結合する水素原子を「脂溶性部位」と位置づけ,その他の極性が高い部位とに切り分けます.
以下でベンジルブロミドについて簡単に見てみます.
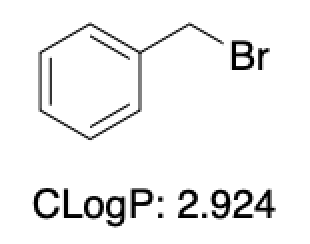
| フラグメント | 寄与 |
|---|---|
| 1 x 臭素 | 0.480 |
| 1 x 脂肪族独立炭素 | 0.195 |
| 6 x 芳香族独立炭素 | 0.780 |
| 7 x 独立炭素上の水素 | 1.589 |
| 1 x 鎖状炭素 | -0.120 |
| 合計 | 2.924 |
MiLogP
MiLogPはMolinspiration社によって開発されたプログラムで,12000以上の分子からなるデータセットをもとに作られています.
- 35の小さな部分構造
- 分子内水素結合や電荷相互作用を記述するための185のより大きい部分構造
といったフラグメントの特徴を有しています.
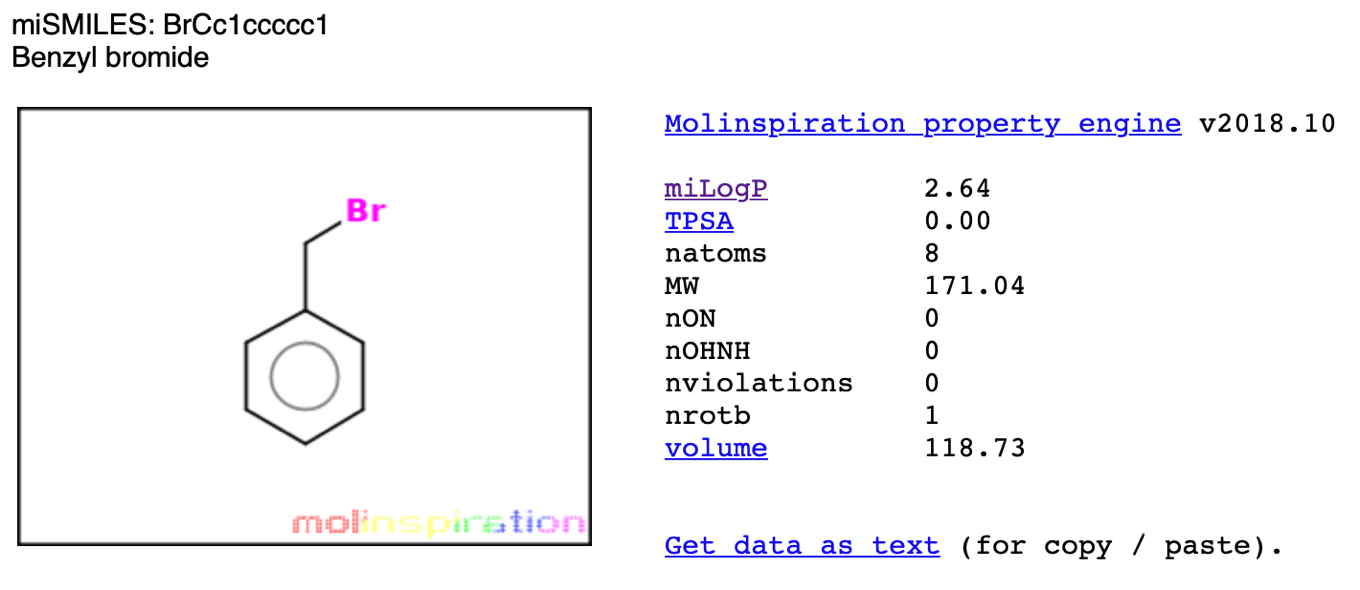
Molinspiration社内のオンラインサービスを用いて先ほどと同様にベンジルブロミドについて計算してみたところ,以下のように「2.64」と計算されました.同じ分子を,同じようなフラグメントをもとに計算するアプローチであっても,異なるアルゴリズム・プログラムを用いると違う値が得られることがおわかり頂けると思います.
原子ごとの寄与を計算するアプローチ
分子を個々の原子にまで分解して,各々の寄与度の合計を計算することでLogPを推定するのがこのアプローチになります.Crippenの研究グループがこのアプローチにおける先駆けと言えます.
$$ \log P = \sum n_{i}a_{i} $$
原子をいくつもの種類にわけることで,異なる化学的環境に置かれた原子の特徴を記述しようとします.また個々の寄与度は実験データへの回帰分析を行うことで決定しています.
原子ごとに寄与を計算するアプローチでは,
- 利点:考慮されないフラグメントが存在しない
- 欠点:正確な記述のために非常に多くの原子タイプを用意する必要がある
- 欠点:分子内の長距離相互作用を記述しにくい
といった特徴が存在します.例えばオリジナルのGhose–Crippenの論文では110もの原子タイプを用いています.
原子ベースのアプローチの代表的な手法(ルール)とプログラムは以下の通りです.
| 手法 | ソフトウェア |
|---|---|
| オリジナルGhose–Crippen(1986–1988) | Dragon ALOGP,MOLCAD,TSAR,PrologP |
| 改良Crippen(1999) | ALOGP98(Discovery Studio,Pipeline Pilot) |
| 補正付きモデル | XLOGP |
改良Crippen(1999)
オリジナルのGhose–Crippenを改良したものがALOGP98プログラムで,「Prediction of Physicochemical Parameters by Atomic Contributions」の論文に報告されています.
RDKitのMolLogPも同じ論文をもとに実装されたものですので,ALOGP98と同様の値を与えるはずです.
XLogP
原子ベースのアプローチの中で唯一補正項を追加しているのがXLOGPアルゴリズムになります.
$$ \log P = \sum_{i=1}^{M} a_{i}A_{i} + \sum_{j=1}^{N} c_{j}C_{j} $$
PubChemに収載されているLogPの値はXLogPをもとにしたものになります.ベンジルブロミドに関しては「XLogP3: 2.9」と記載があります.
XLogPシリーズの最新のモデルは「Computation of Octanol−Water Partition Coefficients by Guiding an Additive Model with Knowledge」という論文に記載されているXLOGP3です.上記のPubChemでもこちらのモデルを使っているようです.
化合物の特徴を中心としたアプローチ
記述子を用いたアプローチ
化合物の構造から容易に計算可能な記述子を使ってLogPを推定する方法は,大量の分子を高速に評価できる点が利点になります.
MLOGP
モリグチらによって開発されたMLOGPでは,脂溶性部位(CX: 重み付け後の炭素とハロゲン原子)と水溶性部位(NO: 窒素・酸素原子)という2つの記述子を用いることで,1230化合物中の実験値のうち73%の変化を記述できることが示されています.
さらに極性芳香族置換基の数,環状構造の有無,ニトロ基の数といった全部で11の補正項を追加することで説明力は91%にまで向上します.
モデルの簡便さとスループットの高さからMLOGPは広く使われています.
ALOGPS
E-state指標(electrotopological index)とはその名の通り,原子の電子分布を表現する記述子です.RDKitではChem.EStateモジュールに実装されています.
TetkoらはE-state指標を用いた一連の研究を発表しています.最新のALOGPS 2.1はVirtual Computational Chemistry Laboratoryのサイトから利用可能です.ベンジルブロミドについて計算を行ってみたところ「2.76」の値を得ました.
量子化学計算または分子動力学計算を用いたアプローチ
logPはオクタノール層と水層における自由エネルギー変化と意味づけられます.
$$ -2.303RT \log P = \Delta G_{oct} – \Delta G_{w} $$
そこで
- 量子化学計算とPCMモデルを用いた自由エネルギーの評価
- 分子動力学法を用いて溶媒を露わにした自由エネルギーの変化を定量する試み
などがなされています.
現状では,計算コストの面から大量の分子を短時間で処理したいケモインフォマティクスの分野でもあまり使われていません.
終わりに
今回は「ケモインフォマティクスとLogP」という話題について,logPの推定法としていくつかの代表的なアプローチを紹介しました.
全ての化合物クラスについてベストな方法は現在のところありませんので,
- フラグメントを用いた方法(CLogPなど)
- 原子ベースの方法(ALogPやXLogPなど)
- 記述子を用いた方法(MLogPやALogPSなど)
からいくつか選んでみて,興味のあるケモタイプと相性のよさそうな手法を使っていくのが良い気がします.
また最近ではSwissADMEのような便利なツールも出てきています.合成を専門とするケミストでも,興味を持って学習を継続していけば色々と分析を行える環境が整いつつあると感じます.
今回は分子構造とLogPをどのように結びつけるかを扱いました.ケモインフォマティクスの分野で精力的に研究されている類似のトピックとして「溶解性の予測」があります(DeepChemのチュートリアルにもあります).次回はこちらを扱ってみたいと思います.
コメント
Dr. Tomさま
とても有用なサイトの運用ありがとうございます。自分は「AI時代を逃げ切ることが可能な50代」の1研究者です(とは言っても来年60)。自分も20-30代では「このまま計算機科学(MO)が進歩したら」と危機感を感じました。30-40代ではケモインフォマティクスに転向し、ニューラルネットワーク法をガリガリやりました。40-50代では化学工学で博士号をとり、50代ではハンセンの溶解度パラメータで著名なハンセン先生と研究をしています。常にコンピュータがこのまま進歩したら化学者なんて仕事が無くなると思ってきましたが、30年たってもそんな事ありませんでした。でも、技術自体は吸収していかないと置いてきぼりを食らうのは確かだと思います。そんな思いもあって自分のHPで情報発信しています。特にケモインフォマティクスの部分では、Tomさまのページとかぶる部分もあるので、ご興味があれば訪れてみてください。
山本様
日本の化学系ウェブを黎明期より牽引されてきた方にコメント頂きまして光栄です.15年程前にJAVAを学んでいた際にPirikaのページに出会って以来,貴サイトにはたびたびお世話になっております.
当時使っていたJAVAやPerlはすっかり忘れてしまいましたが,今やプログラミング非専門家でもライブラリを繋げるだけで動くものが作れる便利な時代になりました.その間に化学の仕事のやり方も少しずつですが変わってきたように思います.
30年後・50年後の「化学者」の仕事には,私自身は楽観的ですし,非常に楽しみです.もっとも仕事の内容は大きく異なったものになるでしょうし,「合成」「分析」といった括りで仕事に従事する人はますます減るでしょう.山本様が仰るように,時代に合わせて技術を吸収していくことが大切なのだと思います.
狭い専門性で一点突破できる胆力がある方はわかりませんが,多くの人にとっては周辺スキルとテクノロジーの進歩を利用しながら生産性を上げていくことが大事かと考えます.色々なものに手を出すと器用貧乏になりがちかもしれませんが,本来の目的を忘れずに精進していきたいと思います.
今後ともよろしくお願いいたします.