「RDKitによる3次元構造の生成」という記事ではSMILESなどから作成したMolオブジェクトから,どのように3次元構造を作り出すかを学びました.その際にRDKitに実装されているアルゴリズムはランダム(stochastic)な手法であるディスタンス・ジオメトリー法を基にしていることにも触れました.今回は1つの分子から複数の構造を生成することにより,分子が取りうる色々な配座について見ていきたいと思います.
必要なライブラリのインポート
まずは必要なライブラリなどのimportをしましょう.今回は「Platinum dataset」の最初の分子を扱うことにします.なお適切な3次元構造の生成には水素原子の存在が重要となりますので,SMILESなどから作成したMolオブジェクトを使用するさいにはChem.AddHsで水素を付加してから作業を行いましょう.
下記の例ではSDFから分子を読み込む際に,removeHs=Falseオプションを設定することで水素原子を保持しています.
# ライブラリのimport
from rdkit import rdBase, Chem
print(rdBase.rdkitVersion) # 2020.09.3
from rdkit.Chem import AllChem
from rdkit.Chem.Draw import IPythonConsole
import py3Dmol
import pandas as pd
# 分子の読み込み
suppl = Chem.SDMolSupplier('./platinum_dataset_2017_01.sdf', removeHs=False)
mols = [x for x in suppl if x is not None]
len(mols) # 4548
mol = mols[0]
今回用いる分子は以下のように,回転可能結合数の多めの化合物です.
コンフォマーの生成
様々な引数によって細かい設定が可能ですが,代表的なものは上にあげた3つになります.すなわち,
- どの分子の3次元構造を生成するか(mol)
- いくつのコンフォマーを生成するか(numConfs)
- どの程度類似した構造を排除するか(pruneRmsThresh)
です.
注意点としては生成したコンフォマーの枝刈り(プルーニング)は指定数のコンフォマーを生成し終わった後に実行されるため,例えば100個のコンフォマーを生成したものの閾値が大きかったために実際には10個のコンフォマーしか得られなかったということがありえます.
EmbedMultipleConfsは実際に得られたコンファオマーのID数をリストで返しますので,そのリストを調べることでいくつのコンフォマーが得られたかがわかります.
下のコードでは1000個のコンフォマーを発生させて,pruneRmsThreshの大きさによってどの程度枝刈りされるかを見てみます.その際randomSeedを設定することによって生成するコンフォマーは同じものが得られるようにしています.
def conf_generation(mol, numConfs, rms):
sm = Chem.MolToSmiles(mol)
m = Chem.MolFromSmiles(sm)
m_h = Chem.AddHs(m)
num_of_confs = []
for i in rms:
confids = AllChem.EmbedMultipleConfs(m_h,
numConfs=numConfs,
randomSeed=1234,
pruneRmsThresh=i,
numThreads=0)
num_of_confs.append((i,len(confids)))
return num_of_confs
rms = [0.5, 1.0, 1.5, 2.0] # 4レベルの閾値設定
num_of_confs = conf_generation(mol, 1000, rms)
| threshold | conformers |
|---|---|
| 0.5 | 1000 |
| 1.0 | 998 |
| 1.5 | 843 |
| 2.0 | 265 |
今回の分子は回転可能な結合数が多めなので,閾値が1.5程度でもほとんどのコンフォマーが残っていますが,もっと自由度の低い分子ではこの限りではありません.
分子力学法による構造最適化
ディスタンス・ジオメトリー法によって生成させた構造は,芳香環が平面構造でないなどの問題を含むために構造最適化を行う必要があるということを「RDKitによる3次元構造の生成」という記事で学びました.今回はRDKitにおける分子力学法の実装について詳しくみていきたいとおもいます.
大きくわけると,
- AllChemに実装されているメソッドによって直接最適化を行う方法
- 最初に力場(フォースフィールド)オブジェクトを作成してから構造最適化を行う方法
の2つに分けられます.構造最適化のみが行いたい場合は前者を,エネルギー計算なども行いたい場合は後者を用いるのがよいでしょう.これはUFF・MMFFともに共通です.
メソッドによる直接最適化
AllChem.MMFFOptimizeMoleculeConfs(mol, numThreads, maxIters)
下のコードでは枝刈りの閾値を2に設定して100個のコンフォマーを生成し,得られたコンフォマー間の重原子RMSを取得しています.十分にばらけた構造が得られていることがわかります.
def mm_opt(mol, ff):
sm = Chem.MolToSmiles(mol)
m = Chem.MolFromSmiles(sm)
m_h = Chem.AddHs(m)
cids = AllChem.EmbedMultipleConfs(m_h,
numConfs=100,
randomSeed=1234,
pruneRmsThresh=2,
numThreads=0)
if ff == 'uff':
AllChem.UFFOptimizeMoleculeConfs(m_h, numThreads=0)
if ff == 'mmff':
AllChem.MMFFOptimizeMoleculeConfs(m_h, numThreads=0)
rmsd = []
m = Chem.RemoveHs(m_h)
for cid in cids:
rmsd.append(AllChem.GetConformerRMS(m, 0, cid))
return rmsd
uff_rmsd = mm_opt(mol, 'uff')
mmff_rmsd = mm_opt(mol, 'mmff')
df = pd.DataFrame({'uff': uff_rmsd,
'mmff': mmff_rmsd})
df.describe().round(2)
| uff | mmff | |
|---|---|---|
| count | 72.00 | 72.00 |
| mean | 2.67 | 2.58 |
| std | 0.57 | 0.60 |
| min | 0.00 | 0.00 |
| 25% | 2.36 | 2.33 |
| 50% | 2.73 | 2.74 |
| 75% | 3.07 | 2.96 |
| max | 3.91 | 3.85 |
フォースフィールドオブジェクトの生成
AllChem.MMFFGetMoleculeForceField(mol, Properties, confId)
UFFとMMFFの違いは力場パラメータが引数に必要かどうかになります.MMFFで必要なパラメータはMMFFGetMoleculePropertiesによって得られます.このようにして作成したフォースフィールドオブジェクトには
- CalcEnergy
- Minimize
という2つのメソッドが実装されていて,それぞれエネルギー計算と構造最適化に用います.エネルギーはkcal/mol単位で表示されます.
下のコードでは,
- 1000個のコンフォマーを発生
- 各コンフォマーをUFFまたはMMFFで構造最適化
- 各コンフォマーのエネルギーを計算
- 最安定構造から順番にソートして(相対エネルギー,コンフォマーID)のタプルのリストを取得
という作業を行っています.
def opt_sp_mm(mol, ff):
# 1. 1000個のコンフォマーを発生
sm = Chem.MolToSmiles(mol)
m = Chem.MolFromSmiles(sm)
m_h = Chem.AddHs(m)
cids = AllChem.EmbedMultipleConfs(m_h,
numConfs=1000,
randomSeed=1234,
pruneRmsThresh=2,
numThreads=0)
# 2,3. 各コンフォマーを最適化し,エネルギー計算
energy = []
if ff == 'uff':
for cid in cids:
uff = AllChem.UFFGetMoleculeForceField(m_h,
confId=cid)
uff.Minimize()
energy.append((uff.CalcEnergy(), cid))
if ff == 'mmff':
prop = AllChem.MMFFGetMoleculeProperties(m_h)
for cid in cids:
mmff = AllChem.MMFFGetMoleculeForceField(m_h, prop,
confId=cid)
mmff.Minimize()
energy.append((mmff.CalcEnergy(), cid))
# 4. エネルギーをソートし,相対エネルギーとIDをリストに格納
energy.sort()
return [(i-energy[0][0],j) for i,j in energy]
uff_e = opt_sp_mm(mol, 'uff')
mmff_e = opt_sp_mm(mol, 'mmff')
5番目までのコンフォマーの結果をまとめたものが下の表になります.
安定なコンフォマーのIDが計算手法によって随分異なるのが気になります.コンフォマー間のエネルギー差も小さいので,本当に異なる構造なのか次のセクションで可視化してみることにしましょう.
| 力場 | エネルギー差(kcal/mol) | コンフォマーID |
|---|---|---|
| UFF | 0.0 | 71 |
| 0.87 | 144 | |
| 1.11 | 164 | |
| 1.16 | 223 | |
| 1.38 | 10 | |
| MMFF | 0.0 | 151 |
| 1.02 | 196 | |
| 1.52 | 170 | |
| 2.40 | 43 | |
| 2.70 | 262 |
コンフォマーの整列
atomIdsをテンプレートとして用いることでどの構造を中心に整列するかを指定できます.RMSlistに空のリストを指定することによってコンフォマー間のRMSリストの一括取得が可能です.
コンフォマーの座標を整列させた後に描画することで,どのあたりの構造が異なるのかが目で見て確認することが可能になるはずです.
今回はベンゼン環部位をテンプレートとして構造を整列させてみます.その際にベンゼン環部位を形成するatomIdが必要になりますが,Mol.GetSubstructMatchを用いることで取得できます.
# コンフォマーを発生させ構造最適化を行う関数
def get_confs(mol, ff):
sm = Chem.MolToSmilesles(mol)
m = Chem.MolFromSmiles(sm)
m_h = Chem.AddHs(m)
cids = AllChem.EmbedMultipleConfs(m_h,
numConfs=1000,
randomSeed=1234,
pruneRmsThresh=2,
numThreads=0)
if ff == 'uff':
for cid in cids:
uff = AllChem.UFFGetMoleculeForceField(m_h,
confId=cid)
uff.Minimize()
if ff == 'mmff':
prop = AllChem.MMFFGetMoleculeProperties(m_h)
for cid in cids:
mmff = AllChem.MMFFGetMoleculeForceField(m_h,
prop,
confId=cid)
mmff.Minimize()
return Chem.RemoveHs(m_h)
# 5つの安定構造のIDを取得
uff_confIds = [j for i,j in uff_e[:5]]
mmff_confIds = [j for i,j in mmff_e[:5]]
# UFF及びMMFFで最適化したコンフォマーを取得
uff = get_confs(mol, 'uff')
mmff = get_confs(mol, 'mmff')
# ベンゼンをテンプレートとして一致部位の取得
core = uff.GetSubstructMatch(Chem.MolFromSmiles('C1=CC=CC=C1'))
# テンプレートを用いてコンフォマーの整列
AllChem.AlignMolConformers(uff, atomIds=core)
AllChem.AlignMolConformers(mmff, atomIds=core)
# コンフォマーを重ね合わせて描画
v = py3Dmol.view(width=600, height=600)
for cid in uff_confIds:
IPythonConsole.addMolToView(uff, confId=cid, view=v)
v.setBackgroundColor('0xeeeeee')
v.zoomTo()
v.show()
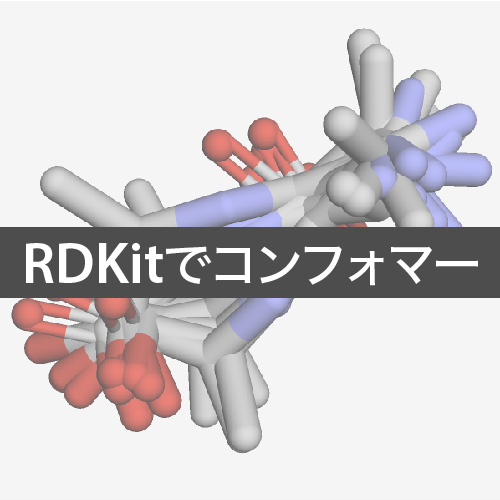
まずUFFで安定化した上位5つの構造です.
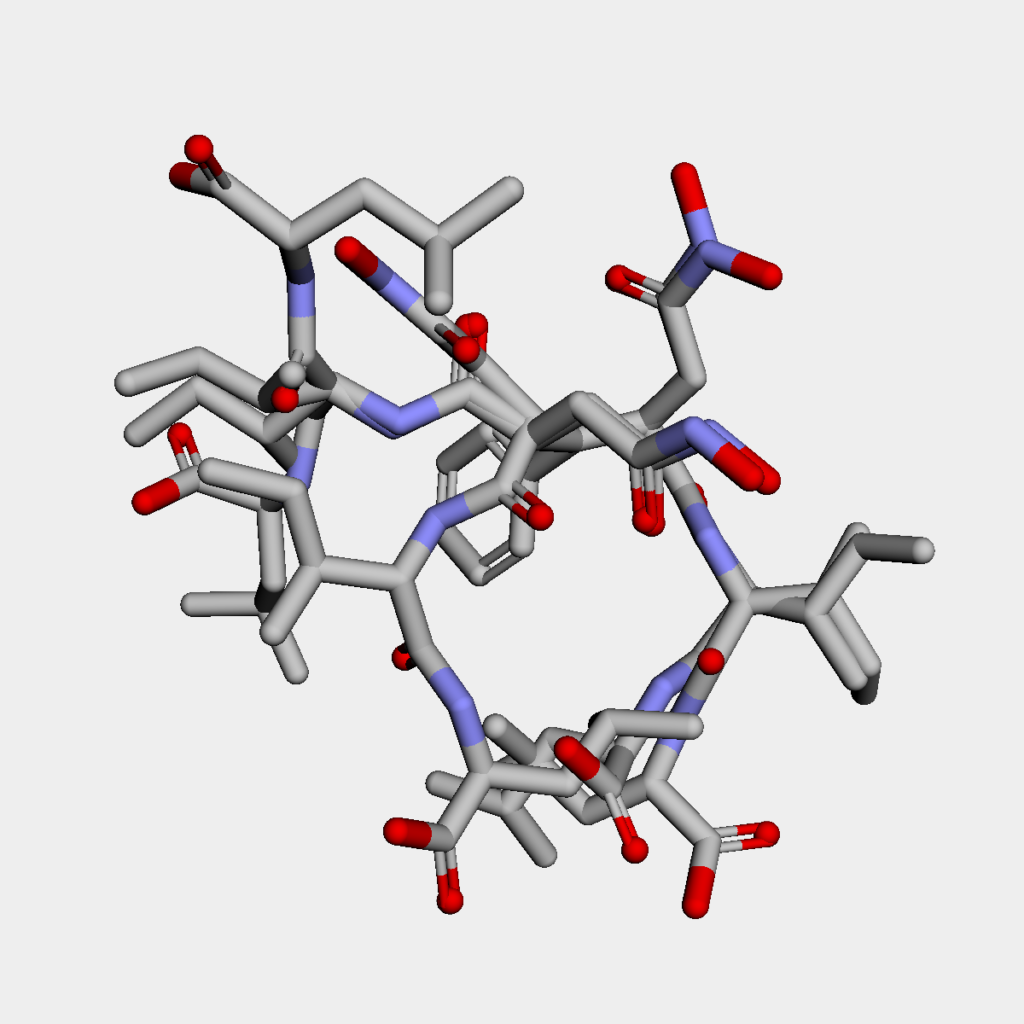
続いてMMFFで安定化した上位3つの構造です.
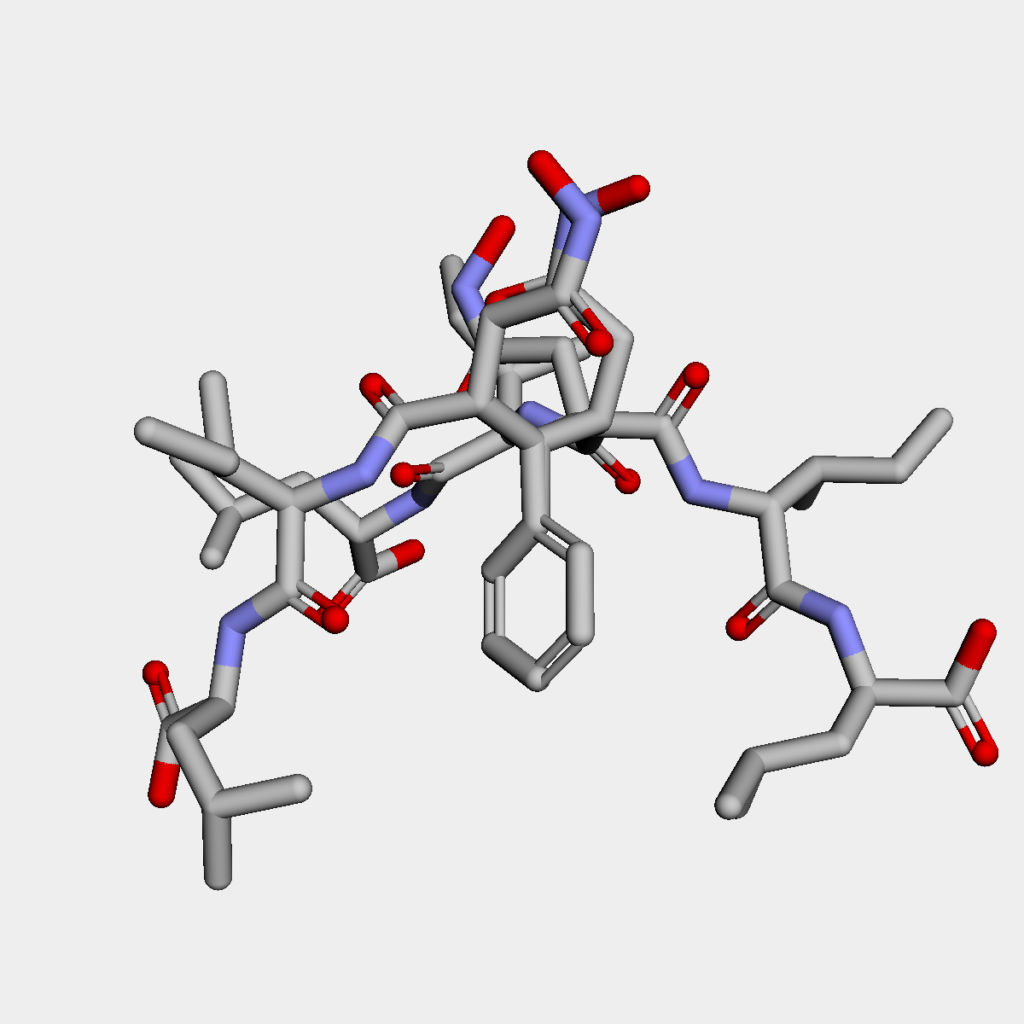
最後に最安定構造同士を重ね合わせたものです.こちらはAllChem.AlignMolを用いて最安定構造同士を整列してから描画しています.
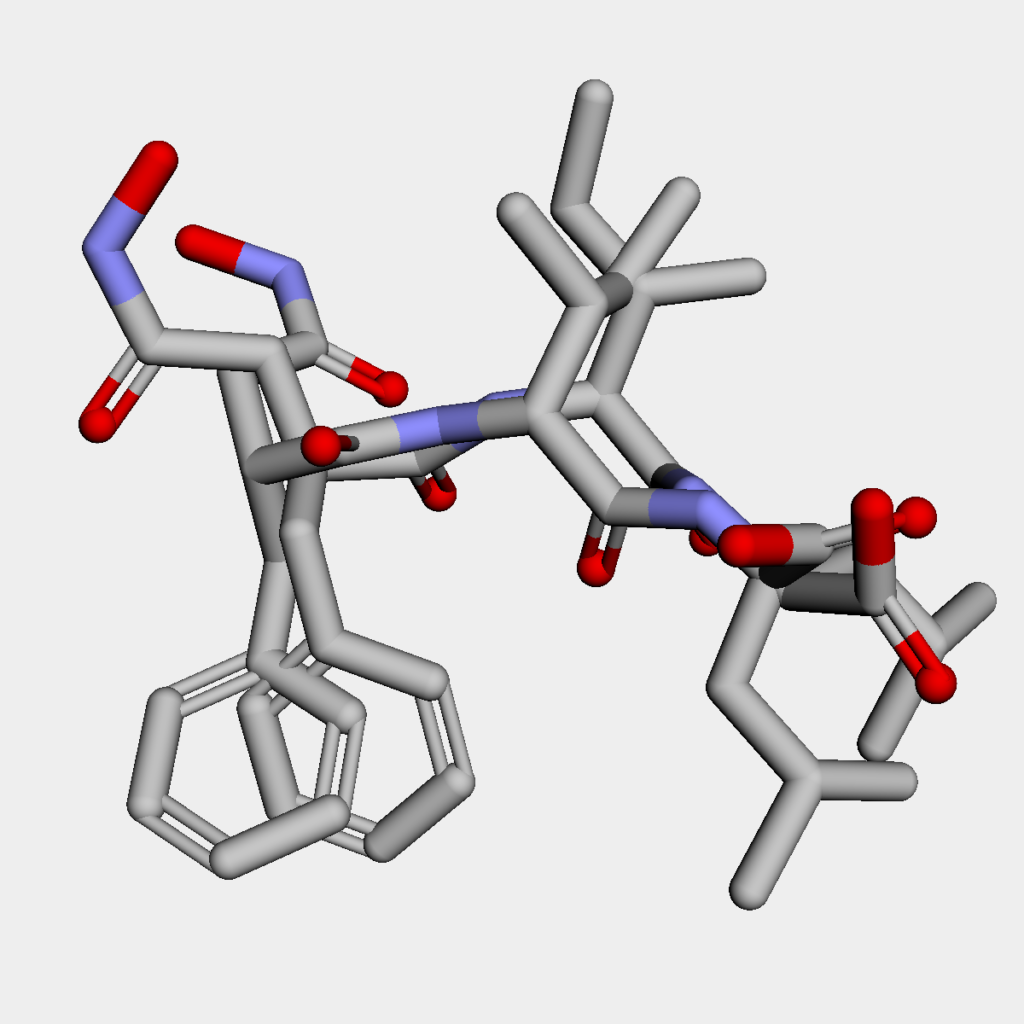
目で見るとすぐにわかりますが,構造が全然違います.結論としては,今回のように回転可能な結合数が多数ある分子を扱う場合には最安定構造を見つけるのは非常に困難です.これはより高レベルの計算手法である分子軌道法やDFTを用いたとしても変わりません.
特に今回はわざわざRMSの閾値を大きめに取ったため,得られてきたコンフォマー間の構造の違いが一層大きくなっています.実際には今回のようなフレキシブルな分子は,エネルギーが低いコンフォマー間の集団(アンサンブル)として振る舞うことから,そのエネルギー差をふまえたボルツマン分布を考慮して分子の性質を考えていく必要があります.
コンフォマーオブジェクトと原子の座標
Mol.GetConformer(id)
Mol.GetConformers()
以前に「RDKitの分子Molオブジェクトを扱う」という記事でRDKitにおける原子であるAtomオブジェクトを扱った際に,プロパティとして原子の座標がなかったことを不思議に思った人がいたかもしれません.
今回見てきたようにMolオブジェクトはいくつものコンフォマーを含む箱のようなものであって,原子の座標を確定させるためには原子番号だけではなく,どのコンフォマーに関する座標かを指定するコンフォマーIDが必要になります.
しかし,これまでにもMolBlockへと分子を書き出す際に原子の座標が表示されていました.実はMolToMolBlockには引数にデフォルトではconfId=-1が設定されているため,特にコンフォマーオブジェクトの存在を意識することなく原子の座標を取得できたのです.従って別のコンフォマーの座標を書き出したい場合には,引数に任意のIDを設定することでMolBlockへと書き出すことが可能です.
コンフォマーオブジェクトの取り扱い
Conformer.GetAtomPosition(atomId)
Conformer.GetPositions()
Conformer.GetOwningMol()
Molオブジェクトに存在するコンフォマーにアクセスするには2つの方法があり,
- IDを指定する方法
- 全てのコンフォマーを一気に取得する方法
があります.いずれの場合にもコンフォマーオブジェクトが得られます.
コンフォマーオブジェクトには原子座標を取得するメソッドや,自身の入れ物であるMolオブジェクトを取得するメソッドなどが設定されています.ここでは簡単に最初の10原子について元素記号と(x,y,z)の座標を表示してみます.シンプルですが色々と他のソフトとの連携が思い描けると思います.
conf = mol.GetConformer(0)
for i, (x,y,z) in enumerate(conf.GetPositions()[:10]):
atom = mol.GetAtomWithIdx(i)
print('{}\tx: {:.2f}\ty: {:.2f}\tz: {:.2f}'.format(atom.GetSymbol(),x,y,z))
C x: -6.30 y: -2.83 z: 0.06 C x: -6.61 y: -1.79 z: -0.81 C x: -5.97 y: -0.56 z: -0.68 C x: -5.03 y: -0.34 z: 0.33 C x: -4.35 y: 1.00 z: 0.46 C x: -2.99 y: 1.03 z: -0.25 C x: -1.85 y: 1.10 z: 0.76 O x: -1.99 y: 1.52 z: 1.91 N x: -0.63 y: 0.66 z: 0.30 C x: 0.56 y: 0.60 z: 1.14
終わりに
今回は「RDKitによるコンフォマーの生成」という話題について,
- Molオブジェクトからのコンフォマー生成の方法
- RDKitにおける分子力学法の取り扱い方
- コンフォマーオブジェクトから原子の座標データを取り出す方法
などを学びました.
次回はMolオブジェクトを用いて算出できる分子記述子について見ていくことで,分子の性質をどのように表現するかを学んでいきます.化学における各記述子は機械学習モデルの特徴量として用いることができ,今後QSARなどのモデルを作成していく際の基礎となります.
>>次の記事:「RDKitにおける記述子の扱い方をリピンスキーの法則を通して学ぶ」
コメント
コンフォマーの整列の部分で質問です。
プログラムを走らせるとuff_H is not difinedと出てしまいます。
原因は何と推測できますか。
blacksuit様
コメントありがとうございます.
ご指摘の通り,「uff_H」という変数が設定されていませんのでエラーが出ているようです.
他の部分はそのままで,「uff_H」を「uff」に変えて頂けますと構造が描画されると思います.
本文の方は修正させて頂きました.
今後ともよろしくお願いいたします.
管理人
なんて早い対応なんだッ‼︎‼︎
表示できました。
ありがとうございます
作成したコンフォマーをmolファイルとして保存するにはどのようにしたら良いでしょうか。
初歩的な質問でしたら申し訳ございません。
コメントありがとうございます.
Molオブジェクトに作成した各コンフォマーにはconfIdを指定することでアクセス可能です.例えば5個のコンフォマーを生成させた場合には0から4まで,5個のconfIdが割り当てられます.
この場合2番目のコンフォマーをmolファイルとして保存したい場合には,
Chem.MolToMolFile(mol, confId=1, filename=’conf_1.mol’)
とすればよく,5番目のコンフォマーを保存する場合には,
Chem.MolToMolFile(mol, confId=4, filename=’conf_4.mol’)
とすればよいです.