ほとんどの分子は3次元空間に広がった立体構造を有していますので,分子の3次元構造を表記することが重要になります.そのために使われる表現方法として大きく
- 直交座標系に沿った表現
- 内部座標に基づいた表現
の2つの座標系の取り方が考えられます.今回はこの2つの方法について見ていきたいと思います.
1つの方法に固執することも可能ですが,目的に応じて適した分子の表現方法は異なりますので,両方の表現方法を理解しておくことが大切になります.
XYZ形式
XYZファイルとは拡張子が「.xyz」となるファイル形式で,各原子の3次元空間における座標をオングストローム単位で記述することで,分子の構造を表現したものになります.直交座標系のXYZ軸に沿った原子の位置を示すことから,デカルト座標系(Cartesian coordinate)とも呼びます.いずれにしろ,外部の座標軸に対する原子の位置関係を記したものです.
特に計算化学の分野でよく使われる入力形式ですが,標準化された規格がないため,ソフトウェアによってそのフォーマットがやや異なるのが難点になります.
原子の座標を与えれば,原子間の距離がわかりますので,どの原子間に「結合」が存在するかを推定することが可能です.そのためXYZ形式のみで分子構造を完全に表現できると言えます.
通常,分子軌道法やDFT計算のインプットファイルにはXYZ形式のみの指定で十分です.一方で分子力学法計算では,各原子に力場パラメータを当てはめる際に結合種類の情報が必要になりますので,結合リストの情報が必要になります.
基本フォーマット
XYZ形式で一般的に広く用いられるフォーマットは下記のようになります.
分子内の原子数 コメント行 元素記号 x座標 y座標 z座標 元素記号 x座標 y座標 z座標 ・・・
中心をなすのが以下の
の部分になります.「MOLファイル・SDFとはどんな化学情報ファイルなのか?」という記事で説明したアトムリストは
という構成をしていましたから,元素記号の位置が異なるだけでほとんど同じものになります.なおXYZ形式ではまれに元素記号の代わりに原子番号を用いるソフトウェアがあります.
複数構造の入力
XYZ形式では1つのファイルに複数構造を収めることが可能です.これを利用することで,塩になっている分子の構造を表現することもできますし,VMDなどのソフトウェアを用いて分子動力学計算(MD)の結果を複数フレームに渡ってアニメーション形式で可視化することも可能になります.
具体的な記法は以下のように空行なしで構造を次々と追記していくだけです.
1つめの原子数 1つめのコメント 元素記号 x座標 y座標 z座標 元素記号 x座標 y座標 z座標 ・・・ 2つめの原子数 2つめのコメント 元素記号 x座標 y座標 z座標 元素記号 x座標 y座標 z座標 ・・・ 3つめの原子数 3つめのコメント ・・・
各フレーム中の原子数は必ずしも一致している必要はありません.そのため,先に述べたように塩のカチオン部位とアニオン部位を分けて記述することができます.
またアニメーション形式で試薬が途中で追加されて,その後脱離基が消滅するようなシーンを再現することも可能です.
XYZファイルの作成方法
3次元構造を扱うフォーマットですので,ChemDrawのような2次元描画系ソフトウェアでは対応していませんが,計算化学系のソフトウェアでは通常XYZ形式での出力に対応しています.
OpenBabel
「Open Babelを使って化学情報フォーマットを変換」という記事で解説したOpenBabelはXYZ形式での出力に対応しています.MOLファイルなどの3次元情報が入ったファイルから変換を行いましょう.

RDKit
RDKitでは直接XYZ形式での出力はできませんでしたが,2019.09のアップデートからXYZ形式での出力に対応しました.
それ以前は各原子の座標を取得することはできますのでprint関数を使うことで間接的にXYZ形式を作成する必要がありました.
下の例では
- PubChemから「アラニン」を検索
- SMILES形式を読み込んでMOLオブジェクト作成
- 3次元構造をETKDGv2で発生
- コンフォマーオブジェクトから各原子の座標を取得
- xyz形式で保存
という一連の流れを行うことで,手動でXYZ形式の出力を行っています.
### ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem
import pubchempy as pcp
print(rdBase.rdkitVersion) ### 2018.09.1
### PubChemからアラニンの情報を取得
alanine = pcp.get_compounds('L-alanine', 'name')
len(alanine) ### 1
alanine = alanine[0]
### Molオブジェクト作成と立体配座の発生
ala = Chem.MolFromSmiles(alanine.canonical_smiles)
ala = Chem.AddHs(ala)
AllChem.EmbedMolecule(ala, AllChem.ETKDGv2())
### 原子の座標を取得してファイルに書き込み
conf = ala.GetConformer(0)
with open('alanine.xyz', 'w') as f:
print(len(ala.GetAtoms()), file=f)
print('Alanine', file=f)
for n,(x,y,z) in enumerate(conf.GetPositions()):
atom = ala.GetAtomWithIdx(n)
print('{}\t{:.2f}\t{:.2f}\t{:.2f}'.format(atom.GetSymbol(), x, y, z), file=f)
作成したalanine.xyzの中身は以下のようです.
13 Alanine C -1.13 -0.63 -0.68 C -0.03 -0.26 0.32 C 1.02 0.57 -0.32 O 1.23 1.73 0.11 O 1.80 0.12 -1.37 N -0.65 0.48 1.38 H -0.78 -0.56 -1.71 H -1.99 0.07 -0.58 H -1.53 -1.63 -0.41 H 0.43 -1.19 0.74 H 2.69 -0.30 -1.12 H -0.48 0.11 2.33 H -0.58 1.50 1.30
Z-マトリックス(Z-matrix)
XYZ形式では直交座標系を基準とした原子の位置を記述したものでした.一方で「原子間距離」,「角度」,「二面角」に基づいて分子内の原子の位置を記述する方法がZ-マトリックスと呼ばれる方法です.基準となる座標軸が分子内に存在することから,内部座標表現(internal coordinate)とも呼ばれています.
XYZ形式と同様に,Z-マトリックスにおいても原子間の結合に関する情報は露わには記載しません.
基本フォーマット
Z-マトリックスのフォーマットはやや複雑です.まず分子内の全ての原子に番号を与えます.その際,原子の位置関係を若い番号の原子との距離・角度・二面角を用いて表現できるように番号を付けていきます.
| 行数 | 原子A | 距離 | 原子B | 角度 | 原子C | 二面角 | 原子D |
|---|---|---|---|---|---|---|---|
| 1 | 元素記号1 | ||||||
| 2 | 元素記号2 | Bとの距離 | B | ||||
| 3 | 元素記号3 | Bとの距離 | B | B,Cとなす角度 | |||
| 4 | 元素記号4 | Bとの距離 | B | B,Cとなす角度 | C | B,C,Dとなす二面角 | D |
| 5 | 以下4行目と同様 |
Z-マトリックスのフォーマットは上の表のようになります.
- 1行目には,1番目の原子の元素記号と「1」を記します.
- 2行目には,2番目の原子の元素記号と「2」を記し,1番目の原子との距離を記します.
これらの作業によって1番目と2番目の原子を通る第1軸(x軸)が定義されます.
- 3行目には,3番目の原子の元素記号と「3」を記し,1または2番目の原子との距離,及び3つの原子からなる角度を記します
これによって1,2,3番目の原子を通る平面を定義し,必然的に第2軸(y軸)を定義したことになります.
- 4行目以降には元素記号と番号を記入し,さらに既存原子との距離・角度・二面角を記していきます.
最初に二面角を定義した段階で,第3軸(z軸)が定義されることになります.なおA-B-C-Dからなる二面角は下のようにB-Cを通して眺めた際に時計回りに定義されていますから,負になることもありえます.
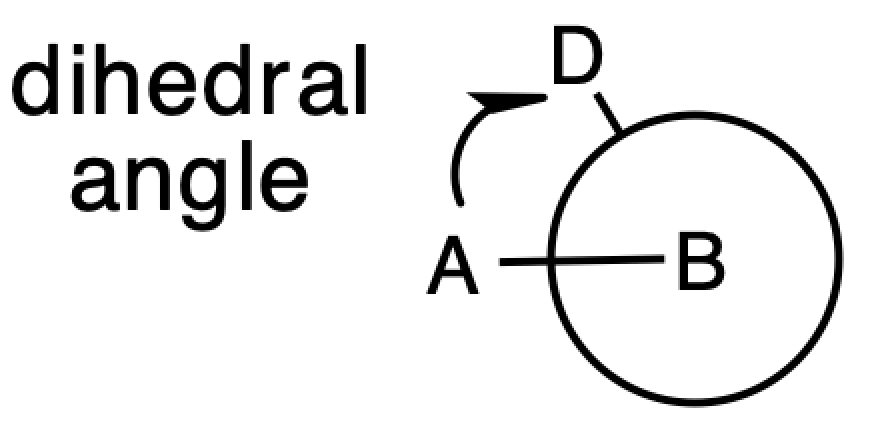
またアセチレンのような直線状の分子では二面角が定義できません.この場合はダミーアトムを定義することで解決するのが一般的です.使い方は例えば「Construction of Z-Matrix:Starting Structure: Acetylene」を参照してみてください.
Z-マトリックスでは,各原子の位置は最初の3つの原子を除くと,既存原子との「距離」「角度」「二面角」によって定義されています.すなわち,原子数Nからなる分子は「3N – 6」のパラメータによって定義されることがわかります.これは分子の「自由度」にほかなりません.
具体例:1,2-ジクロロエタン
それでは具体的に1,2-ジクロロエタンのZ-マトリックスを構築してみます.原子の番号は以下のように振ることとしました.
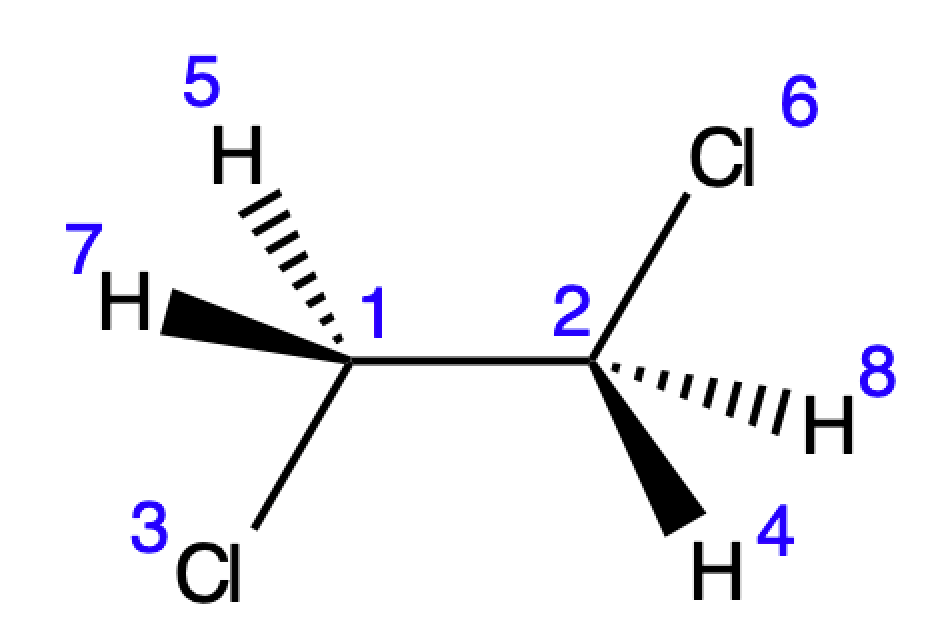
C1 C2 1.5 1 Cl3 1.7 1 109 2 H4 1.1 2 109 1 -60 3 H5 1.1 1 109 2 180 4 Cl6 1.7 2 109 1 60 5 H7 1.1 1 109 2 -60 6 H8 1.1 2 109 1 180 7
今回の例のように比較的小さな分子ですと,紙に構造を書いたものをZ-マトリックスへと変換することは容易ですが,ある程度以上の大きさの分子になるとZ-マトリックスの構築は非常に困難です.そのため,現実的には直交座標系で表現された分子をZ-マトリックスに変換した方が楽です.
XYZ形式とZ-マトリックスの相互変換
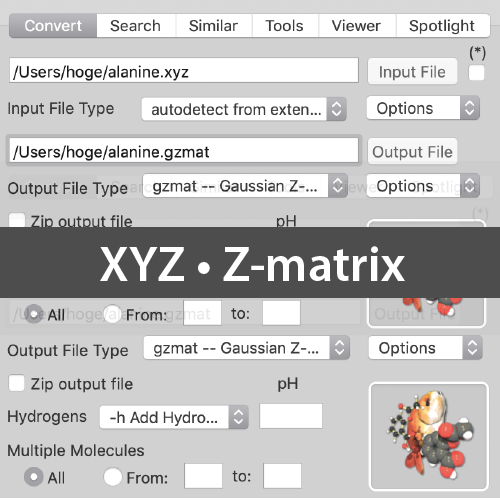
XYZ形式とZ-マトリックスは,同じ情報を異なる座標軸を用いて表現したに過ぎませんので相互変換が可能です.実施したい計算などによってはZ-マトリックスを用いた入力ファイルが必要な場合がありますが,ここでもOpenBabelが利用できます.
先ほどRDKitを用いて作成した「alanine.xyz」をZ-マトリックス形式に変換してみます.
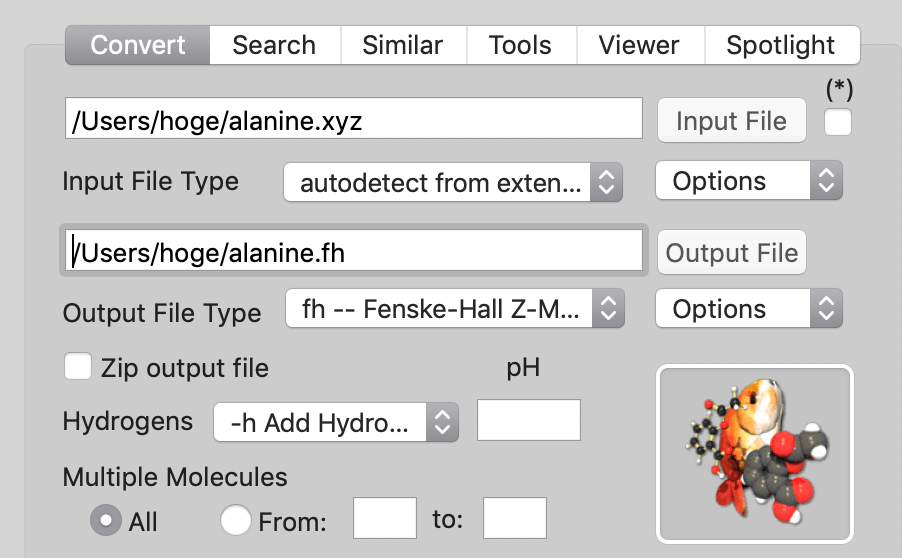
いくつかのZ-マトリックスを含んだ形式が用意されていますが,ここでは「Fenske-Hall Z-Matrix」という形式を選択してみました.
得られたファイルは以下のようでした.最初の行を削れば基本的にはZ-マトリックス形式になっていますが,やや原子番号を変更していく必要がありそうです...
13 C 1 C 1 1.532 C 2 1.484 1 111.206 O 3 1.255 2 119.196 1 118.7 O 3 1.383 2 122.994 1 297.9 N 2 1.434 1 107.263 3 119.9 H 1 1.090 2 111.760 3 21.6 H 1 1.113 2 110.130 3 262.8 H 1 1.110 2 108.509 3 147.9 H 2 1.119 1 109.837 3 238.5 H 5 1.015 3 116.227 2 266.8 H 6 1.034 2 115.065 1 125.8 H 6 1.026 2 115.224 1 262.6
量子化学計算におけるデカルト座標とZ-マトリックス
構造最適化の収束には座標の選び方が重要になります.原子の位置に応じて分子のエネルギーは決定されます.構造最適化はこのエネルギーを最小化するように原子の位置を少しずつずらしていく作業です.つまり分子の自由度,3N-6個を変数とした最適化問題です.
一般的にデカルト座標よりも内部座標の方を用いた方が最適化の収束が速いと言われていますが,それは内部座標の結合長や結合角などが分子に働く力の方向をよく表しているからだと考えられます.
最適化に用いる座標系は量子化学計算ソフトのオプションで設定可能です.例えばGaussianでは入力座標系によらず指定可能です.以下に簡単に説明します.
内部座標を最適化
Gaussianでのデフォルト設定になります.デカルト座標・Z-マトリックスのいずれの方法で入力構造を作成しても,Gaussianが自動的に内部座標に変換し,それを最適化していきます.
入力ファイルで指定したZ-マトリックスに沿って最適化を行わせたい場合にはopt=z-matrixのオプションを指定します.
デカルト座標で最適化
こちらの場合も入力構造は,デカルト座標・Z-マトリックスのいずれの方法でも可能です.opt=Cartesianオプションを設定することで,デカルト座標系を用いた最適化が行われます.
終わりに
今回は分子の立体構造を表現する方法としてXYZ形式とZ-マトリックス形式を解説しました.どちらかと言えばケモインフォマティクスよりも計算化学の分野で用いられる形式ですので,今後本サイトで量子化学計算を扱っていく際の基礎となると思います.
またコンピューターで分子の情報を扱う際に非常によく使われるフォーマットとして,SMILES記法と呼ばれる表現方法があります.こちらも併せて理解を深めておくとよいでしょう.
>>次の記事:「SMILES記法は化学構造の線形表記法」
コメント