これまで本ブログでは,pythonの機械学習用ライブラリであるscikit-learnを用いて,回帰タスクである化合物の溶解度予測に取り組むことで,機械学習について学んできました.
- 線形モデルを用いた化合物の溶解度予測:通常最小二乗法,Ridge回帰,Lasso回帰
- 交差検証を用いてElastic Netを化合物の溶解度データに対して最適化
- データ分析と前処理:パイプライン処理で化合物の溶解度を推定
今回は最小二乗法による線形モデルについて,確率モデルとして取り扱うことで理解を深めていきたいと思います.分析にはpythonの統計モデル用パッケージであるstasmodelsを用いていきます.
「ESOL: Estimating Aqueous Solubility Directly from Molecular Structure」
J. Chem. Inf. Comput. Sci. 2004, 44, 1000–1005.
(DOI: 10.1021/ci034243x)
ESOLの論文で用いられている記述子
データセットの引用元であるEstimated SOLubility(ESOL)の論文では,
- clogP
- 分子量:MW
- 回転可能結合数:RB
- 芳香族指数:AP
- 非炭素原子数の比:NC
- 水素結合ドナー数:HD
- 水素結合アクセプター数:HA
- 極性表面積:PSA
の8つの記述子を用いて重回帰分析を行い,「各パラメータの重要さをt値の絶対値によって評価」することで最初の4つの記述子に絞り込み,最終的に以下の回帰式を得ています.
$$ Log(S_w) = 0.16 – 0.63 \times clogP – 0.0062 \times MW + 0.066 \times RB -0.74 \times AP $$
今回はclogPをRDKitのMolLogPで,PSAをTPSAで代用することとし,statsmodelsを用いてモデル構築を行っていきます.
必要なライブラリのインポートと分子の準備
まずは必要なライブラリのインポートと分子の読み込みを行い,その後必要な記述子の計算を行いましょう.
以下のコードでは
- ライブラリのインポート
- pandasのデータフレームとして情報を読み込む
- 分子MOLオブジェクトの構築
- 各記述子の計算
という順番で作業を行っています.
# 1. ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, Descriptors
from rdkit.Chem.Draw import IPythonConsole
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
print(rdBase.rdkitVersion) # 2019.03.3
import statsmodels
print(statsmodels.__version__) # 0.9.0
# 2, 3. pandasデータフレームとして読み込み
df = pd.read_csv('./ci034243xsi20040112_053635.txt')
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='SMILES')
df.columns = ['ID', 'm_sol', 'p_sol', 'SMILES', 'ROMol']
# 4. 記述子の計算
## 分子の炭素数を数える関数
def GetNumCarbons(mol):
count = 0
for atom in mol.GetAtoms():
if atom.GetSymbol() == 'C':
count += 1
return count
## 記述子の計算
df['logP'] = df.ROMol.map(Descriptors.MolLogP)
df['MW'] = df.ROMol.map(Descriptors.MolWt)
df['RB'] = df.ROMol.map(Descriptors.NumRotatableBonds)
df['AP'] = df.ROMol.map(lambda x: len(x.GetAromaticAtoms())/x.GetNumHeavyAtoms())
df['NC'] = df.ROMol.map(lambda x: 1 - GetNumCarbons(x)/x.GetNumHeavyAtoms())
df['HA'] = df.ROMol.map(Descriptors.NumHAcceptors)
df['HD'] = df.ROMol.map(Descriptors.NumHDonors)
df['TPSA'] = df.ROMol.map(Descriptors.TPSA)
続いてデータセットを訓練用とテスト用に分割し,各記述子間の相関を眺めておきます.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df[['logP', 'MW', 'RB', 'AP', 'NC', 'HA', 'HD', 'TPSA']],
df.m_sol, random_state=0)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# ((858, 8), (286, 8), (858,), (286,))
fig = plt.figure()
sns.heatmap(data=X_train.corr().round(2), annot=True, vmax=1, vmin=-1, cmap='bwr')
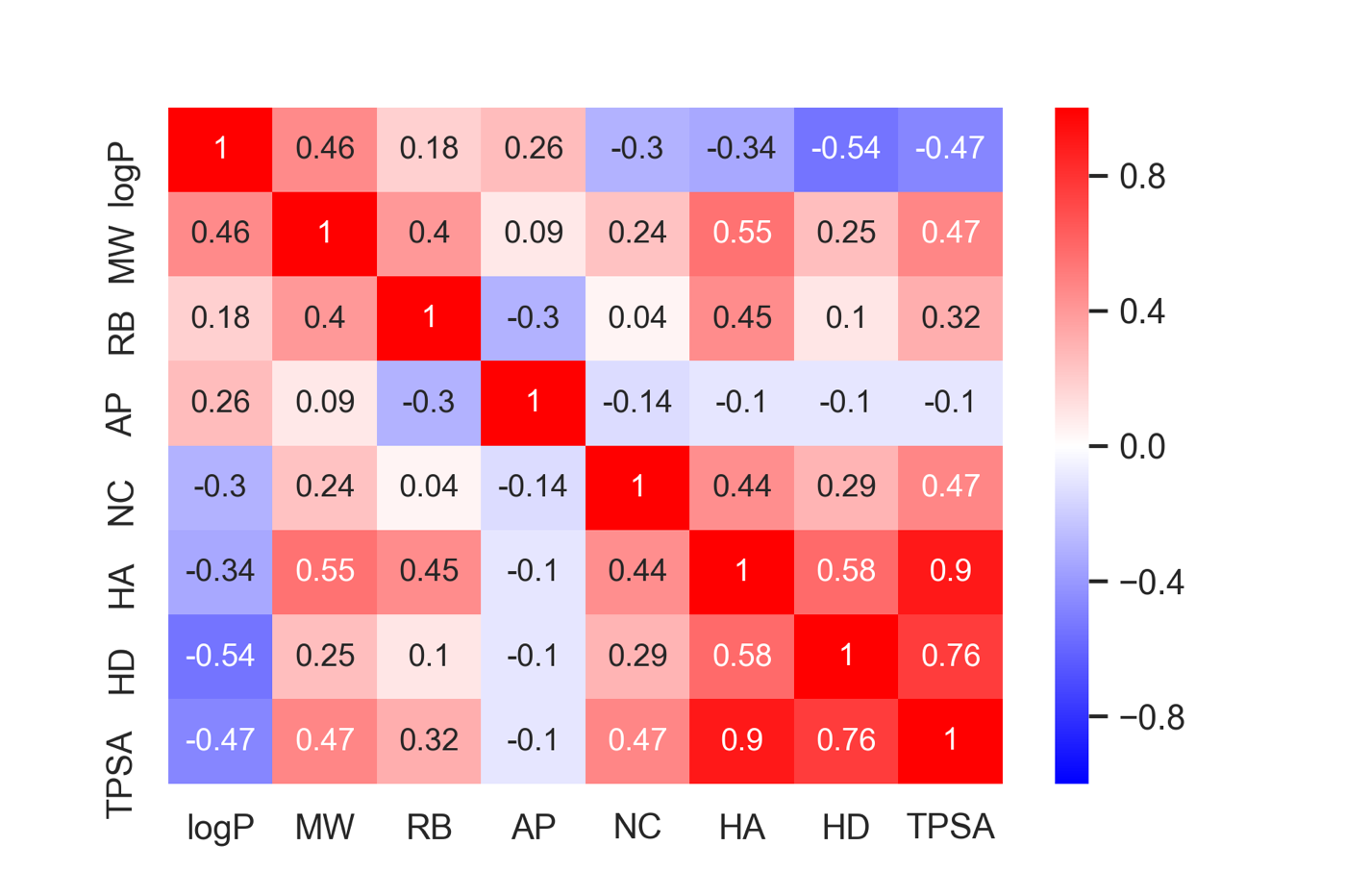
TPSAとHAやHDとの相関が強いことが確認できます.
statsmodelsを用いたモデルの作成
statsmodelsでは2つの方法で作成するモデルの形を指定できますが,ここでは統計分析によく使われるR言語と似たように記述できるAPIを利用していきます.formulaを「m_sol ~ logP + MW」と指定することは,
$$ solubility = \beta_{0} + \beta_{1} \times logP + \beta_{2} \times MW $$
の形で最小二乗法を行っていくことに相当します.
FULLモデルの作成
まずは8個全ての記述子をモデル作成に使用してみましょう.statsmodelsではデータが全て同一のpandasデータフレーム中にあることが前提となっていますので,まずX_trainとy_trainをまとめて1つのデータフレームにしています.
X_y_train = X_train.join(y_train)
full_model = smf.ols('m_sol ~ logP + MW + RB + AP + NC + HA + HD + TPSA', data=X_y_train).fit()
full_model.summary().tables[1]
作成したモデルのsummary関数には色々な情報が含まれていますが,とりあえず各記述の係数などについての情報を取り出しました.
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.1206 | 0.100 | 1.202 | 0.230 | -0.076 | 0.318 |
| logP | -0.7835 | 0.053 | -14.822 | 0.000 | -0.887 | -0.680 |
| MW | -0.0063 | 0.001 | -7.069 | 0.000 | -0.008 | -0.005 |
| RB | 0.0160 | 0.018 | 0.890 | 0.374 | -0.019 | 0.051 |
| AP | -0.2721 | 0.115 | -2.365 | 0.018 | -0.498 | -0.046 |
| NC | 1.1567 | 0.236 | 4.894 | 0.000 | 0.693 | 1.621 |
| HA | 0.2031 | 0.046 | 4.447 | 0.000 | 0.113 | 0.293 |
| HD | -0.0546 | 0.054 | -1.012 | 0.312 | -0.160 | 0.051 |
| TPSA | -0.0158 | 0.003 | -5.363 | 0.000 | -0.022 | -0.010 |
表中のt値やp値の意味は,「記述子の係数がゼロであるモデル(帰無仮説)」に対して,係数がゼロではない確率をt検定した値になります.つまりp値が低ければモデルに意味のある情報を加えている記述子と理解してよいです.
ESOLの論文には「t値の絶対値をもとに記述子を選択」し,4つに絞り込んだと記載がありますが,今回作成したモデルでは「回転可能結合数:RB」が必要なさそうです.これは今回用いたデータセットは論文で利用されているもののうち,特に分子量の低いもの(RBの値が極端に小さいデータセット)に限られているからと思われます.
ESOLモデルの作成
フルモデルと同様にして,「logP」「MW」「RB」「AP」の4つの記述子を用いたモデルの作成もしてみましょう.
esol_model = smf.ols('m_sol ~ logP + MW + RB + AP', data=X_y_train).fit()
print(esol_model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: m_sol R-squared: 0.766
Model: OLS Adj. R-squared: 0.765
Method: Least Squares F-statistic: 700.0
Date: Mon, 16 Sep 2019 Prob (F-statistic): 1.25e-267
Time: 12:34:24 Log-Likelihood: -1229.1
No. Observations: 858 AIC: 2468.
Df Residuals: 853 BIC: 2492.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.2109 0.085 2.493 0.013 0.045 0.377
logP -0.7200 0.021 -33.933 0.000 -0.762 -0.678
MW -0.0068 0.000 -16.714 0.000 -0.008 -0.006
RB 0.0191 0.015 1.239 0.216 -0.011 0.049
AP -0.3762 0.113 -3.329 0.001 -0.598 -0.154
==============================================================================
Omnibus: 24.925 Durbin-Watson: 2.055
Prob(Omnibus): 0.000 Jarque-Bera (JB): 56.010
Skew: -0.055 Prob(JB): 6.88e-13
Kurtosis: 4.247 Cond. No. 802.
==============================================================================
「データ分析と前処理:パイプライン処理で化合物の溶解度を推定」という記事ではscikit-learnを用いて最小二乗法を行い,以下の式を得ました.今回も乱数の種を同じに設定したため,全く同じ式が得られました.
$$ Log(S’_w) = 0.21 – 0.72 \times clogP – 0.0068 \times MW + 0.019 \times RB -0.38 \times AP $$
多重共線性(multicollinearity)
今回のような重回帰分析を行う際,説明変数(記述子)の数を増やすほど決定係数が高くなりやすいため,たくさんの説明変数を入れ込んだモデルを作成しがちです.このような場合に気をつけるべき点として「多重共線性」が挙げられます.
多重共線性とは,説明変数間で相関係数が高い場合に生じる現象です.相関の高い複数の変数は同じような情報を持っているため,作成したモデルにおける係数の大小や符号などの解釈が難しくなってしまいます.一般的には相関係数が0.8を超える場合には注意が必要と言われています.先ほどの調べたようにPTSAとHAの相関係数が0.9でしたので,注意が必要そうです.
分散拡大要因(VIF:Variance Inflation Factor)
独立変数間の相関係数行列の逆行列の対角要素を分散拡大要因(VIF)と呼び,多重共線性の存在をチェックするために使われます.VIFが10を超える独立変数は,多重共線性の原因となる可能性が高く,モデル構築の際には除去する方が好ましいと言われます.
先ほど,各記述子間の相関係数を眺めてみましたが,ここではVIFを求めてみましょう.statsmodels.stats.outliers_influenceにもvariance_inflation_factorという関数が実装されていますが,今回はnumpyを用いて逆行列を計算してみます.
corr_mat = np.array(X_train.corr()) inv_corr_mat = np.linalg.inv(corr_mat) pd.Series(np.diag(inv_corr_mat), index=X_train.columns)
logP 9.185386 MW 7.814513 RB 2.046585 AP 1.405224 NC 1.495421 HA 8.925479 HD 3.408831 TPSA 10.326682 dtype: float64
TPSAのVIFが10を超えているため,モデル構築の際には取り除くほうがよさそうです.
赤池情報量規準:AIC
重回帰分析においては,どの記述子の組み合わせを用いたモデルを最善として選択するかは自明ではありません.ESOLの論文で行われていたように,FULLモデルからt値の小さい記述子を除去していく方法(t検定)も一つの方法です.今回は「赤池情報量規準(AIC:Akaike’s Information Criterion)」と呼ばれるものを用いてモデル選択を行っていこうと思います.類似の多数ありますが,AICが最もよく使われます.
AICは
$$ AIC = -2 \times (最大対数尤度 – 推定されたパラメータ数) $$
で表される指標で,AICが小さいほど「よい」モデルとみなされます.尤度はパラメータ数を増やすと大きくなりやすいため,用いるパラメータ数に罰則をつけています.そのため不必要なパラメータが含まれていないモデルが選ばれやすいと言えます.
AICは先ほどのstasmodelsで作成したモデルのsummary関数でも表示されますし,model.aicで直接アクセスすることも可能です.
statsmodelsを用いた重回帰分析
全探索
今回の場合はTPSAを除くと記述子の数が7個ですので,全ての組み合わせを考えて最も小さいAICを与えるモデルを選択することが現実的です.pythonで組み合わせを考える場合にはitertools.combinationsを用いるのが便利です.下記のコードでは
- generate_formulas関数で記述子の組合せから作成するモデルのformulaを生成
- modeling_linear関数でformulaに従ってモデルを作成
- 記述子ゼロのNullモデルを別個作成,評価
- for文中で利用する記述しを変化させながらモデルを作成,評価
- AICの値でソート
という順番で処理をしています.
desc_list = ['logP', 'MW', 'RB', 'AP', 'NC', 'HA', 'HD']
def generate_formulas(descriptors, num):
import itertools
if num > len(descriptors):
return None
else:
for f in itertools.combinations(descriptors, num):
formula = 'm_sol ~ ' + ' + '.join(f)
yield formula
def modeling_linear(formula, data):
model = smf.ols(formula=formula, data=data).fit()
return formula, model
n_var = []
formula = []
model = []
AIC = []
adj_r2 = []
## Nullモデル作成
null_model = smf.ols(formula='m_sol ~ 1', data=X_y_train).fit()
n_var.append(0)
formula.append('m_sol ~ 1')
model.append(null_model)
AIC.append(null_model.aic)
adj_r2.append(null_model.rsquared_adj)
## 利用する記述子の数を変えながらモデル作成
for i in range(1,9):
for f in generate_formulas(desc_list, i):
eq, m = modeling_linear(formula=f, data=X_y_train)
n_var.append(i)
formula.append(f)
model.append(m)
AIC.append(m.aic)
adj_r2.append(m.rsquared_adj)
df_model = pd.DataFrame({'n_var': n_var,
'formula': formula,
'model': model,
'aic': AIC,
'adj_r2': adj_r2})
## AIC評価で上位5つ
df_model.aic.sort_values()[:5]
df_model.formula[df_model.aic.sort_values()[:5].index]
print(df_model.model[df_model.aic.idxmin()].summary().tables[1])
124 2427.719766
127 2429.333483
121 2430.013110
106 2431.414490
103 2434.607337
Name: aic, dtype: float64
124 m_sol ~ logP + MW + AP + NC + HA + HD
127 m_sol ~ logP + MW + RB + AP + NC + HA + HD
121 m_sol ~ logP + MW + RB + AP + NC + HD
106 m_sol ~ logP + MW + AP + NC + HD
103 m_sol ~ logP + MW + RB + NC + HD
Name: formula, dtype: object
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0857 0.101 0.850 0.396 -0.112 0.284
logP -0.6995 0.047 -14.783 0.000 -0.792 -0.607
MW -0.0076 0.001 -8.799 0.000 -0.009 -0.006
AP -0.3739 0.103 -3.639 0.000 -0.576 -0.172
NC 0.9648 0.236 4.084 0.000 0.501 1.428
HA 0.0749 0.031 2.381 0.018 0.013 0.137
HD -0.1798 0.049 -3.675 0.000 -0.276 -0.084
==============================================================================
これより,「logP」「MW」「AP」「NC」「HA」「HD」の6つを用いたモデルが最もAICが低かったようです.P値の値も大丈夫そうです.
ステップワイズ法(stepwise regression)
前項のような全探索は変数の数が増えてくると現実的ではありません.そこで体系的にモデルを改善していく方法としてよく使われるものに,ステップワイズ法と呼ばれるものがあります.
ステップワイズ法では全ての変数を組み入れたFullモデルを作成し,そこから1つの変数を取り除いたモデルを作成します(今回は7種類).もっともAICの低いモデルを採用し,変数6個のモデルとします.そこからまた1つの変数を取り除いたモデルを作成し,,,と繰り返し改善が見られなくなった点で探索を終了します.逆に変数0のNullモデルから出発し,1つずつ変数を足していくステップワイズ法も考えられます.
今回はFullモデルから始めるステップワイズ法を,R言語のstepAIC関数に類似したpython関数として実装します.
def stepAIC(descs_l):
import copy
descriptors = descs_l
f_model = smf.ols(formula='m_sol ~ ' + ' + '.join(descriptors), data=X_y_train).fit()
best_aic = f_model.aic
best_model = f_model
while descriptors:
desc_selected = ''
flag = 0
for desk in descriptors:
used_desks = copy.deepcopy(descriptors)
used_desks.remove(desk)
formula = 'm_sol ~ ' + ' + '.join(used_desks)
model = smf.ols(formula=formula, data=X_y_train).fit()
if model.aic < best_aic:
best_aic = model.aic
best_model = model
desc_selected = desk
flag = 1
if flag:
descriptors.remove(desc_selected)
else:
break
return best_model
model_a = stepAIC(desc_list)
print(model_a.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0857 0.101 0.850 0.396 -0.112 0.284
logP -0.6995 0.047 -14.783 0.000 -0.792 -0.607
MW -0.0076 0.001 -8.799 0.000 -0.009 -0.006
AP -0.3739 0.103 -3.639 0.000 -0.576 -0.172
NC 0.9648 0.236 4.084 0.000 0.501 1.428
HA 0.0749 0.031 2.381 0.018 0.013 0.137
HD -0.1798 0.049 -3.675 0.000 -0.276 -0.084
==============================================================================
今回はステップワイズ法を用いても同じモデルに落ち着きました.
作成したモデルの評価
statsmodels.api.qqplot(data, line=None)
線形モデルでは「実験データを,モデルで説明できる部分と誤差部分」に分け誤差部分が正規分布に従うと仮定しています.そのため,作成した回帰モデルがきちんとデータを説明できているかを理解するためには,残差の正規性を調べることが大切になります.
以下のコードではステップワイズ法で得たモデルの残差を可視化し,正規分布の確率密度関数と重ね合わせています.またscipy.statsに実装されているShapiro-Wilkの正規性検定による確認も行っています.
from scipy import stats predict = model_a.predict() resid = model_a.resid rvs = stats.norm.pdf x = np.linspace(-5,5,100) fig = plt.figure() ax1 = fig.add_subplot(111) sns.distplot(resid) ax1.plot(x, rvs(x), 'k--', lw=1) ## Shapiro–Wilk test stats.shapiro(resid)
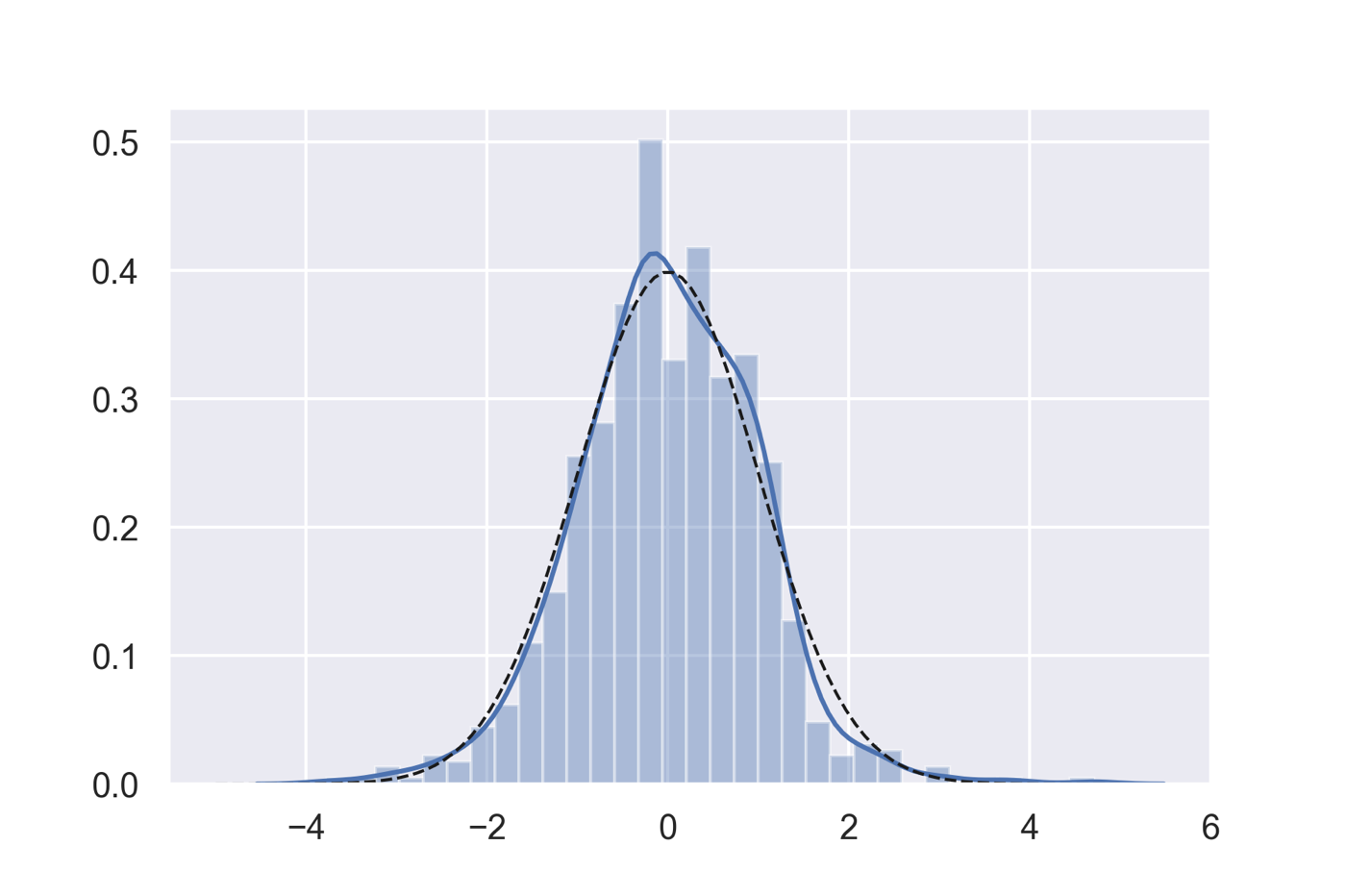
(0.9898769855499268, 1.2270874321984593e-05)
またQ–Qプロットと呼ばれる,理論上の正規分布における分位点と実際のデータの分位点を散布図としてプロットしたグラフで確認することもあります.Qは「Quantile」の略になります.statsmodels.apiにはqqplotというそのものズバリな関数が実装されています.
fig = sm.qqplot(resid, line='s')
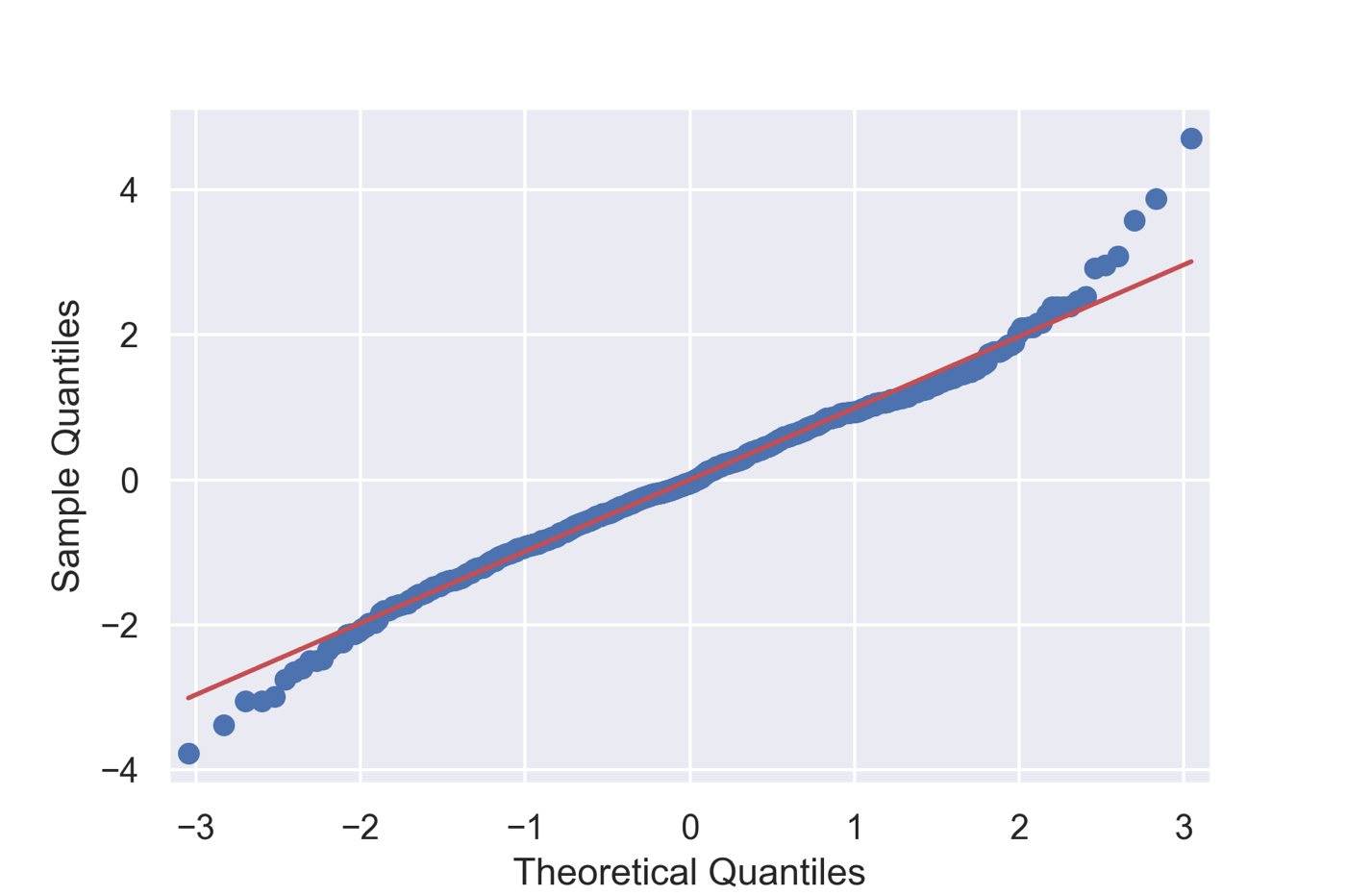
残差は正規分布に従うと結論してよさそうです.
終わりに
今回は「pythonのstatsmodelsを使った重回帰分析で溶解度予測:AICによるモデル選択」という話題について,
- statsmodelsを用いた線形モデル作成の方法
- 多重共線性について
- 赤池情報量規準について
- ステップワイズ法によるモデル選択
- 残差の正規性に関する確認
などについて説明しました.特にこれまで本ブログではあまり用いてこなかったstatsmodelsは,pythonで統計モデリングを行う際の最重要ライブラリーの1つですので,使い方に習熟していきたいところです.
次回は線形モデルに関する理解をさらに深めるべく,statsmodelsを用いたロジスティック回帰について扱っていきたいと思います.
>>次の記事:「pythonで一般化線形モデル:statsmodelsを用いたロジスティック回帰で化合物の変異原性予測」

コメント