これまで「RDKitとscikit-learnで機械学習:変異原性をk-最近傍法で予測」という記事から3回に渡り,化合物の変異原性の有無を予測する「2クラス分類」の機械学習モデルを構築してきました.
今回は教師あり学習のもう1つの柱である「回帰」と呼ばれる問題を扱います.具体的には化合物の溶解度を予測する機械学習モデルを,「線形モデル」というアルゴリズムを用いて考えていきます.
「ESOL: Estimating Aqueous Solubility Directly from Molecular Structure」
J. Chem. Inf. Comput. Sci. 2004, 44, 1000–1005.
(DOI: 10.1021/ci034243x)
線形モデルとは
線形モデルは入力ベクトルの線形関数として予測を行うモデルになります.すなわち,ターゲットの値が特徴量の線形和として表すことができるという仮定の下にモデルを構築します.数式としては下記のように表すことができます.なおyの上に「^」がついているのは予測値であることを意味します.
$$ \hat{y} = w_0 + w_1 x_1 + w_2 x_2 + … + w_n x_n $$
このような特殊とも言える仮定を考えていますが,線形モデルは非常に強力です.特にデータポイントに対して特徴量の方が多いようなデータセットでは容易に過剰適合してしまいます.
線形回帰
最も古典的な線形モデルが「通常最小二乗法」(Ordinary Least Squares)と呼ばれるものになります.
下のような二次元のデータポイント20点を考えてみます.この場合線形モデルでは
$$ \hat{y} = ax + b $$
と表せます.これはxy平面における直線を表しますが,aとbの組み合わせによって下の図のように青・黒・赤の破線を含めてたくさんの直線の引き方が考えられます.それではどのようにaとbを決めればよいでしょうか?
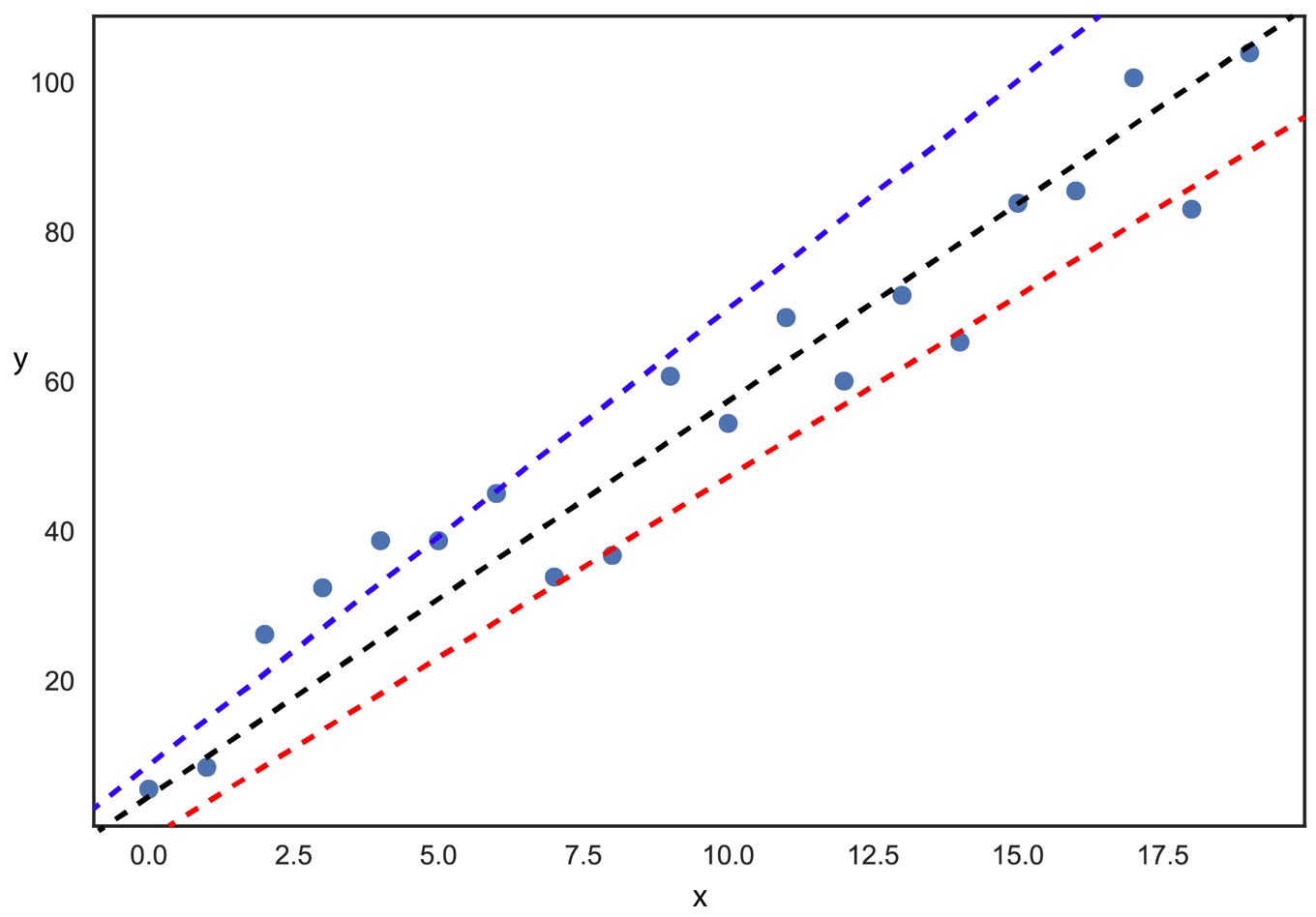
最も精度のよい直線は,「予測値と真の値の差の和を最小にする直線」と考えることができます.つまり平均二乗誤差(Mean Squared Error)をaとbの関数と考えて最小を与える組み合わせを考えればよいわけです.
すなわち,
$$ MSE(a,b) = \frac{1}{20} \sum_{i=1}^{20} ((ax_{i} + b) – y)^{2} $$
を最小化します.
機械学習ではこのようにある関数の誤差を最小にするようなパラメータを考えることが多く,このような関数を「損失関数」または「誤差関数」と呼びます.
通常最小二乗法における損失関数の一般式は下記のようになります.なおwは切片を含む係数のベクトル,xは特徴量xj(j=1,2,,,n)からなるベクトルです.
$$ Loss(Ols) = MSE(w) = \frac{1}{m} \sum_{i=1}^{m} (w^{T}\cdot x^{i} – y^{i})^2 $$
Ridge回帰
先ほど線形モデルは過剰適合しやすいと述べました.モデルの複雑さを抑えるために行う処理を「正則化」といいます.具体的には損失関数に正則化項を加えた関数を考え,この関数を最小化するようなパラメータを求めることを考えます.またこのような「損失関数+正則化項」をコスト関数と呼びます.
Ridge回帰では線形モデルにおける各項の係数の大きさに関してペナルティを与えます.αは正則化におけるペナルティの程度を調節するパラメータで,大きいほどモデルの制限が強くなり,0だと通常最小二乗法と同じモデルになります.
$$ Cost(Ridge) = MSE(w) + \alpha \frac{1}{2} \sum_{i=1}^{n} w_{i}^2 $$
後者の正則化項は係数ベクトルのL2ノルム
$$ \frac{1}{2} (||w||_{2})^{2} $$
と書けますので,L2正則化と呼ばれます.Ridge回帰では各係数をできるだけ小さく抑えるようにモデルを制限します.
Lasso回帰
Lasso回帰でも線形モデルの各項の係数の大きさに関してペナルティを与えます.Ridge回帰ではL2正則化を行いましたが,係数ベクトルのL1ノルムによる正則化を行うのがLasso回帰と呼ばれるものになります.αは同様にペナルティの程度を表すパラメータです.
$$ Cost(Lasso) = MSE(w) + \alpha \sum_{i=1}^{n} |w_{i}| $$
Lasso回帰では正則化の結果,多くの係数がゼロになります.
scikit-learnにおける線形モデルの実装
sklearn.linear_model.Ridge(alpha)
sklearn.linear_model.Lasso(alpha)
上述した通常最小二乗法,Ridge回帰,Lasso回帰は全てsklearn.linear_modelに実装されています.
必要なライブラリのインポートと化合物の読み込み
まずはデータセットから分子を読み込み,分子の情報を入力ベクトルとして変換しましょう.
論文のデータはコンマ区切りのテキストファイルで,「化合物名」「溶解度の実験値」「(論文中の)溶解度の予測値」「SMILES」の4つのデータが1144化合物について格納されています.
以下のコードでは
- 必要なライブラリのインポート
- pandasのデータフレームとして情報を読み込む
- SMILESからRDKitのMOLオブジェクトを構築
- Morganフィンガープリントを入力ベクトルとして準備
- データセットを訓練用とテスト用に分割
という処理を行っています.
## 1. ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, Descriptors, Descriptors3D
from rdkit.Chem.Draw import IPythonConsole
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt
print(rdBase.rdkitVersion) # 2018.09.1
mpl.style.use('seaborn')
## 2. データフレームとして読み込み
df = pd.read_csv('./ci034243xsi20040112_053635.txt')
df.head()
読み込んだデータフレームは以下のようになります.
| Compound ID | measured log (solubility:mol/L) |
ESOL predicted log (solubility:mol/L) |
SMILES | |
|---|---|---|---|---|
| 0 | 1,1,1,2-Tetrachloroethane | -2.18 | -2.794 | ClCC(Cl)(Cl)Cl |
| 1 | 1,1,1-Trichloroethane | -2.00 | -2.232 | CC(Cl)(Cl)Cl |
| 2 | 1,1,2,2-Tetrachloroethane | -1.74 | -2.549 | ClC(Cl)C(Cl)Cl |
| 3 | 1,1,2-Trichloroethane | -1.48 | -1.961 | ClCC(Cl)Cl |
| 4 | 1,1,2-Trichlorotrifluoroethane | -3.04 | -3.077 | FC(F)(Cl)C(F)(Cl)Cl |
## 3. MOLオブジェクトの構築
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='SMILES')
## 4. フィンガープリントの作成
morgan_fps = []
for mol in df.ROMol:
fp = [x for x in AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)]
morgan_fps.append(fp)
morgan_fps = np.array(morgan_fps)
morgan_fps.shape # (1144, 2048)
target_sols = df['measured log(solubility:mol/L)']
target_sols.shape # (1144,)
## 5. データセットの分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(morgan_fps, target_sols, random_state=0)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# ((858, 2048), (286, 2048), (858,), (286,))
線形回帰
まずは通常最小二乗法を用いてモデルを構築してみます.
from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, y_train)
print('acc on train: {:.3f}'.format(lr.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(lr.score(X_test, y_test)))
acc on train: 0.983 acc on test: -52194037948843663818752.000
訓練データに対する精度は高いですが,テスト用データの精度がマイナスです.データからモデルは何も学ぶことができていないようですので,モデルの複雑度を下げる必要があります.
Ridge回帰
続いてL2正則化を用いたRidge回帰を用いてモデル構築をしてみます.繰り返しになりますが,Ridge回帰では係数の絶対値が小さく抑えられます.
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print('acc on train: {:.3f}'.format(ridge.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(ridge.score(X_test, y_test)))
acc on train: 0.959 acc on test: 0.637
今度はきちんと学習できているようですが,まだ過剰適合の様子が見てとれます.そこでαの値をデフォルトの1から変化させてみましょう.大きな値にすることで過剰適合を抑えることができるはずです.
for i in [0.0001, 0.001, 0.1, 1, 5, 10, 50, 100]:
r = Ridge(alpha=i).fit(X_train, y_train)
print('-- alpha = {} --'.format(i))
print('acc on train: {:.3f}'.format(r.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(r.score(X_test, y_test)))
-- alpha = 0.0001 -- acc on train: 0.983 acc on test: 0.209 -- alpha = 0.001 -- acc on train: 0.983 acc on test: 0.231 -- alpha = 0.1 -- acc on train: 0.981 acc on test: 0.493 -- alpha = 1 -- acc on train: 0.959 acc on test: 0.637 -- alpha = 5 -- acc on train: 0.902 acc on test: 0.694 -- alpha = 10 -- acc on train: 0.859 acc on test: 0.695 -- alpha = 50 -- acc on train: 0.706 acc on test: 0.632 -- alpha = 100 -- acc on train: 0.613 acc on test: 0.570
今回の場合ですとαが5と10の間あたりが最適そうですが,大事なのは小さくするとモデルが過剰適合しやすく,大きくするとモデルが強く制限されるという傾向を確認することです.
Lasso回帰
続いてL1正則化を用いたLasso回帰を見てみます.
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print('acc on train: {:.3f}'.format(lasso.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(lasso.score(X_test, y_test)))
acc on train: 0.000 acc on test: -0.000
訓練データにおいても精度が出ていませんのでデフォルトのαの値ではモデルに制限が強すぎるようです.そこでαの値を小さくして,モデルを複雑にしてみます.
for i in [0.00001, 0.0001, 0.001, 0.005, 0.01, 0.1, 1]:
l = Lasso(alpha=i, max_iter=100000).fit(X_train, y_train)
print('-- Lasso: alpha = {} --'.format(i))
print('acc on train: {:.3f}'.format(l.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(l.score(X_test, y_test)))
-- Lasso: alpha = 1e-05 -- acc on train: 0.983 acc on test: 0.224 -- Lasso: alpha = 0.0001 -- acc on train: 0.980 acc on test: 0.480 -- Lasso: alpha = 0.001 -- acc on train: 0.932 acc on test: 0.644 -- Lasso: alpha = 0.005 -- acc on train: 0.794 acc on test: 0.666 -- Lasso: alpha = 0.01 -- acc on train: 0.706 acc on test: 0.647 -- Lasso: alpha = 0.1 -- acc on train: 0.228 acc on test: 0.207 -- Lasso: alpha = 1 -- acc on train: 0.000 acc on test: -0.000
小さすぎるαの場合には最小二乗法モデルに近づき過剰適合していますが(alpha = 1e-05),徐々に大きくしていくとテスト用データにおける精度が上がっていき,あるところで再び下がる(alpha = 0.1)といった傾向が見てとれます.
各モデルの比較
linear_model.intercept_
最後に各正則化法によってモデルがどのように変化していくかを係数の大きさで見ていきたいと思います.訓練したモデルに対して,
- coef_で各特徴量に対する係数
- intercept_で切片
にアクセス可能です.下のコードでは2048bitのMorganフィンガープリントのうち,最初の300bitについての係数を比較することでモデル毎の傾向を眺めてみます.
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
lasso0005 = Lasso(alpha=0.0005).fit(X_train, y_train)
r = 300
x = range(len(lr.coef_[:r]))
plt.scatter(x, lr.coef_[:r], marker='o', s=50, alpha=0.7, label='linear reg')
plt.scatter(x, ridge10.coef_[:r], marker='x', s=50, alpha=0.7, label='ridge')
plt.scatter(x, lasso0005.coef_[:r], marker='v', s=50, alpha=0.7, label='lasso')
plt.legend(loc='best', frameon=True)
plt.xlim(0,len(lr.coef_[:r]))
plt.xlabel('Fingerprint')
plt.ylabel('Coefficient')
plt.ylim(-3.5, 3.5)
下が係数をプロットしたものになります.線形回帰の場合は絶対値が大きいため,2つを除いてグラフ範囲に収まっていません.
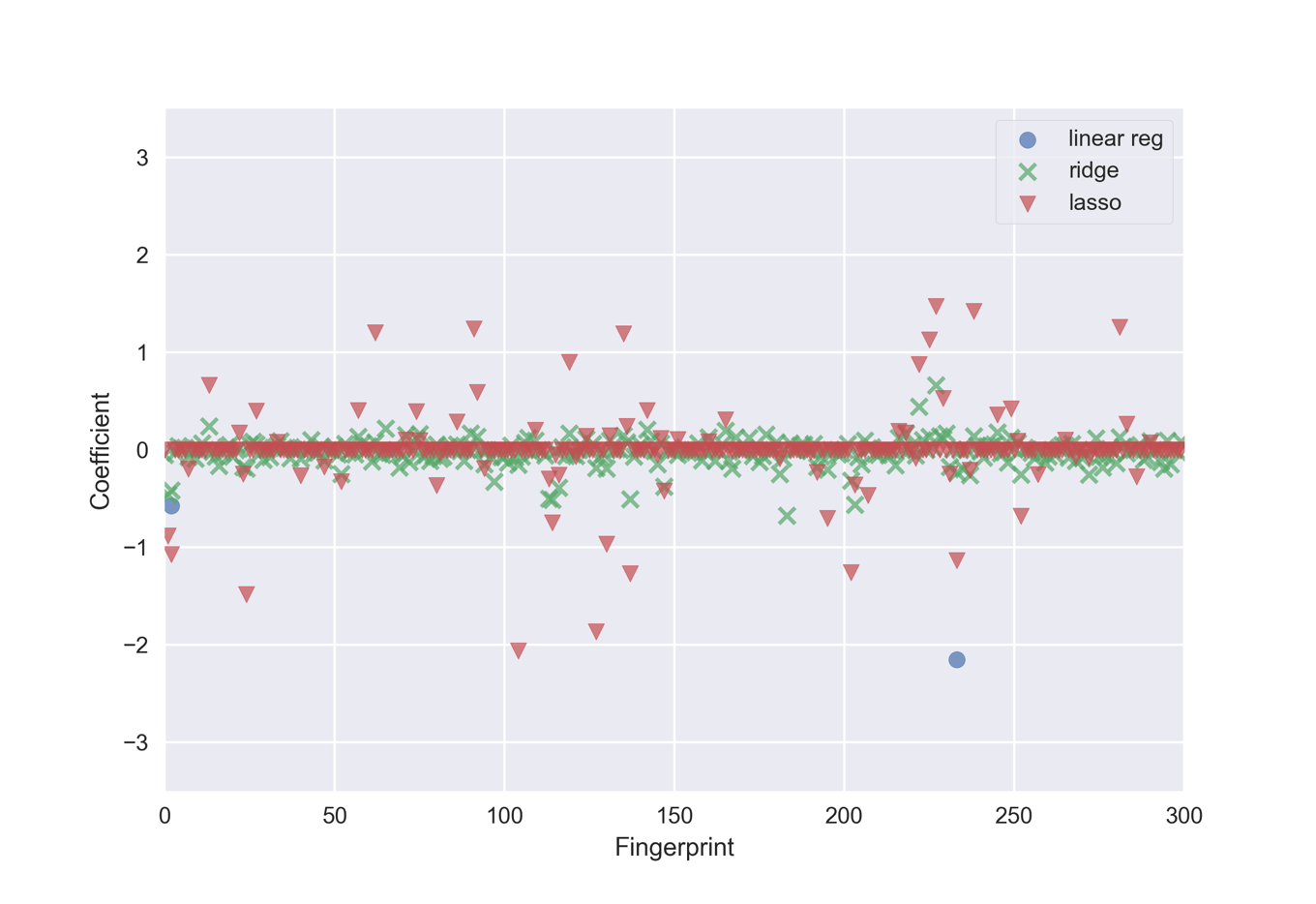
一般的に
- 線形回帰では過剰適合しやすいため係数が非常に大きくなる
- Ridge回帰では係数が全体的に小さく抑えられる
- Lasso回帰ではほとんどの係数がゼロになり,一部の特徴量のみがモデル構築に使われる
という傾向が言えます.
正則化法としてはRidgeを第一選択にしつつ,一部の特徴量のみが大事だとわかっている場合にはLassoを使うのがよいと言われます.
終わりに
今回は「線形モデルを用いた化合物の溶解度予測:通常最小二乗法,Ridge回帰,Lasso回帰」という話題について,
- 線形モデルとは何か
- 線形モデルの正則化法
- scikit-learnを用いた線形モデルの実装について
といった内容について学びました.特に化合物の溶解度予測を行いながら,
- L2正則化を行うRidge回帰では係数の絶対値が小さく抑えられること
- L1正則化を行うLasso回帰では多くの係数をゼロにすることで,特徴量の選択を行うこと
を触れました.またモデルハイパーパラメーターであるαを変化させることで,モデルの精度が大きく変化することを見てきました.
今回は同じ訓練データを用いてハイパーパラメーターをスクリーニングし,テスト用データを用いて精度を確認しました.一般的にはこれでは「テスト用データをパラメータのチューニングに使用してしまっている」ため,未知のデータに対する精度はテスト用データに対して得られたものよりも低くなります.
次回はRidge回帰とLasso回帰を組み合わせた「Elastic Net」と呼ばれるモデルを用いて,「クロスバリデーション」と「グリッドサーチ」について説明していくことで,どのようにハイパーパラメーターを最適化していくかについて学んでいきたいと思います.

コメント