これまでケモインフォマティクス用ライブラリであるRDKitを用いて,分子記述子やフィンガープリントを用いた化合物のベクトル化方法を学んできました.
また分子のベクトル表現を入力として,いくつかの機械学習アルゴリズムを用いた変異原性や溶解度の予測モデル作成も行いました.
今回も機械学習モデルの1つである,ニューラルネットワークについて学んでいきます.近年,大きく話題を集めているディープラーニング(深層学習)はニューラルネットワークで構成される機械学習モデルになります.
まずニューラルネットワークの構成要素を説明し,その後でディープラーニング用フレームワークの1つであるTensorflowを用いて実際にモデル作成を行っていきます.単純な構成のネットワークから徐々に複雑なネットワークを構築していく過程で,過学習・正則化・ハイパーパラメーター最適化などの重要な概念を学んでいきます.
化学とディープラーニング(深層学習)
化学の分野でディープラーニングが大きく注目を集めるきっかけとなったのは,2012年に行われたKaggleの機械学習コンペ「Merck Molecular Activity Challnege」です.このコンペでは,深層学習を取り入れたモデルがランダムフォレストなどの他の方法ベースのモデルを抑えて優勝しました.
Merckではそれまでランダムフォレストを用いて様々なQSARモデルを構築していたようですが,この結果を受けてニューラルネットワークのQSARタスクにおける力量を精査する論文を発表しています.
また「Tox21は米国の大規模毒性学プロジェクト:HTSによるアッセイ結果は機械学習コンペで用いられたデータセット」という記事でも述べたように,NIH主催で行われた「Tox21データチャレンジ2014」でも深層学習モデルが多数の部門で優勝を飾りました.
これ以降ケモインフォマティクス分野におけるディープラーニングの研究・適用事例が多く報告されるようになり,現在では発表される論文のかなりの数がディープラーニングを利用したものになっています.
ニューラルネットワークの構成
よく見られるニューラルネットワークの模式図を下に示します.このネットワークは
- 入力層
- 中間層(隠れ層)
- 出力層
と呼ばれる層から構成されています.
この図では情報は左から右に流れており,入力層の情報が2つの中間層を通りながら出力層へ入り,何らかの値(予測活性値など)が出力されていく様子を示しています.
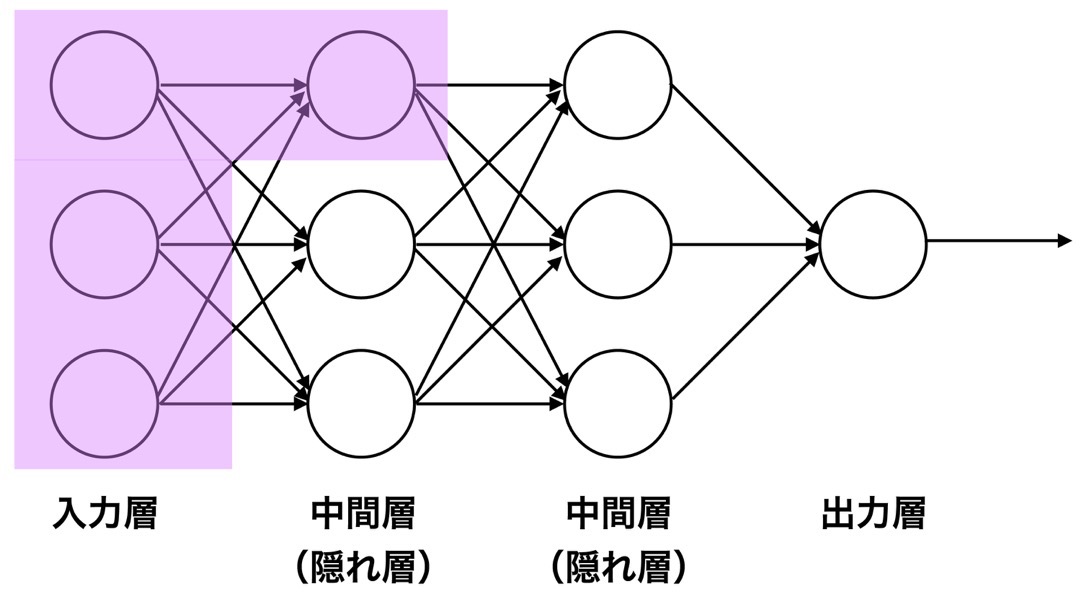
それでは上図で紫色にハイライトしている部分に着目して,もう少しニューラルネットワークの中身を見ていきたいと思います.
ニューラルネットワークの重みとバイアス
紫色でハイライトしている部分の詳細を示したものが下図になります.
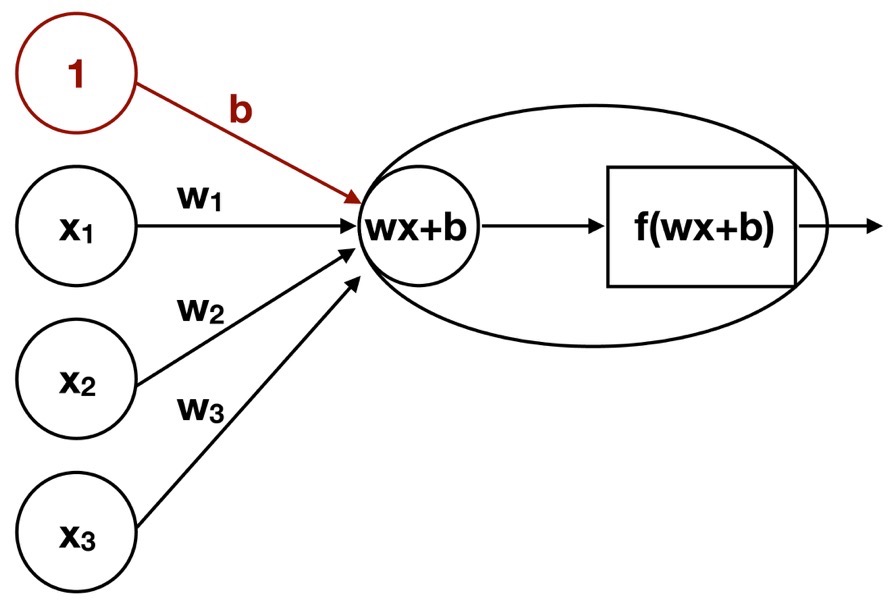
入力層(x1, x2, x3)の3つのニューロンに加えて,バイアスと呼ばれる茶色で示したニューロンが加わっています.また出力先のニューロンの中身もそのまま次の層へと出力されるのではなく,四角(f)で記した関数を挟んでから次の層へと向かっています.
入力層の各ニューロンの情報は,重み(weight)を乗じて次の層へと伝達されます.上の場合は,3つのニューロンからそれぞれ情報を受け取りますので,バイアスbを加味すると
$$ \omega_1 \times x_1 + \omega_2 \times x_2 + \omega_3 \times x_3 + b $$
の値が伝達されます.
ここで重みとバイアスは学習を進めていく過程で変化していくニューラルネットワークの変数になります.
入力ベクトルを
$$ x^T = \left( x_1, x_2, x_3 \right) $$
重みベクトルを
$$ \omega = \left( \omega_1, \omega_2, \omega_3 \right) $$
とすると,
$$ \omega x + b $$
のように記せます.
なおバイアスを加えない形のネットワークも存在します.
活性化関数
重みとバイアスを用いて表現された入力は,何らかの処理を施してから次の層へと渡されます.この処理を行う関数を「活性化関数」と呼びます.上図の四角で示した部分になります.
このように各ニューロンは
- 前の層から情報を受け取り
- 活性化関数で処理をし
- 次の層へ情報を渡す
という段階的な作業を行っていますが,簡略化のためネットワーク図を描くときはバイアス・活性化関数を省略して描くのが普通です.
入力値をそのまま返す「恒等関数」は通常は回帰タスクの出力層でのみ使われ,他の部分では何らかの「非線形関数」が用いられます.非線形関数による変換を繰り返すことが,ニューラルネットワークのデータに合わせた柔軟な学習を可能にしています.
よく使われる活性化関数としては,シグモイドやtanhの他,ReLU(Rectified Linear Unit)と呼ばれる関数があります.
ニューラルネットワークの損失関数
ニューラルネットワークの学習は,モデルのパラメータである重みとバイアスを変化させていくことで,モデルの出力を正しい値に近づけていくことで行われます.
この学習の指標として使われるのが「損失関数」になります.損失関数はモデルの性能の悪さを表しており,その値を小さくしていくことで良いモデルを目指すことになります.
よく使われる損失関数としては,
- 回帰タスクで使われる平均二乗誤差(MSE)
- クラス分類で使われる交差エントロピー
が挙げられます.
ニューラルネットワークの学習
ニューラルネットワークは重みとバイアスをパラメータとしたモデルです.損失関数もこれらパラメータに依存しています.損失関数は複雑な形をしていますので,その値を最小にするパラメータの組合せを解析的に一発で求めることは不可能です.そこで使われるのが,勾配を利用して逐次的に損失関数を減少させる方向にパラメータを動かしていく方法,すなわち勾配法になります.
ディープラーニングでは,誤差逆伝搬法と呼ばれる方法を用いて計算を行っていきます.最適化手法としては,シンプルな
- 確率的勾配法(SGD)
の他,その発展系である
- RMSProp
- Adam
など色々なものが使われます.
- どの最適化手法を用いるか
- どの程度の学習率を用いるか
はモデルのハイパーパラメーター(人間が決める値)になります.
ニューラルネットワークの評価関数
評価関数はモデルの良さ・悪さを評価するという点では損失関数と似ています.損失関数はモデルの学習に用いられますが,評価関数は学習には用いられないという違いがあります.
そのため,
- 損失関数は数学的に学習しやすい関数
- 評価関数は人間が値を見て理解しやすい関数
が使われる傾向にあります.具体的な評価関数としては,
- 精度:ターゲットに対する正しい予測の割合
- 適合率:選択した項目がどの程度複数クラス分類に関連しているか
- 再現率:複数クラス分類において,特定クラスに関する精度
などが挙げられます.
深層学習とフレームワーク
TensorflowとPyTorch
実際に私たちがニューラルネットワークを使ってモデルを作成する際には,今まで挙げたような要素が既に部品として用意されている深層学習用のフレームワークを使ってモデルを組み立てていくことがほとんどです.
これまで色々なフレームワークが開発されていますが,2020年4月現在ポピュラーなものは
の2つです.双方ともお互いの良い部分を取り込みながら進化してきているため,現在では基本的な使い方に関してはそれほど差がなくなってきました.
現状におけるこれらフレームワークを取り巻く主な違いとしては,
- Tensorflowの方がユーザー数が多く,ウェブ・書籍含めサンプルコード数が多い
- PyTorchは研究コミュニティで多く使われており,論文と同時に実装が公開させることが多い
ことが挙げられます.論文著者の実装がTensorflowのみであっても,有志によってPyTorch実装がすぐに公開されることも頻繁にあります(少なくとも化学に関しては逆はあまりないように思います).
グラフニューラルネットワーク
分子構造が数学的なグラフであることから,化学分野に関してはグラフ上でのディープラーニング(Graph Convolutional Network; GCN)の適用が盛んに行われています.自分でフレームワークを用いて実装することも可能ですが,グラフ構造が扱いやすいように設計されていて,色々な形のネットワークが最初から用意されているライブラリーを用いる方が簡便です.
この観点では深層学習フレームワークChainerをベースとして化学分野に特化したライブラリーであったChainer Chemistryが特徴的でしたが,残念ながら2019年末に開発中止となってしまいました.
Tensorflowベースとして初期に登場したライブラリーとしてDeepChemが挙げられますが,現状ではうまくコミュニティを取り込むことができていないように思えます.PyTorchベースに書き直す計画(?)も含めて,現在抜本的に改定を行おうとしており,これからどのような形になっていくか不透明です.
一方でPyTorchベースのグラフ関連ライブラリーとしては,
の2つが,2020年春時点では拮抗しているように見受けられます.前者の方が対応モデルが多いですが,後者の方がAPIがきれいで人気が出てきているようです.
どのフレームワークを使うか
ほんの2年前は,PyTorchが研究分野で現在のように勢いをつけてくるとは正直想像していませんでした.幸いにもニューラルネットワークがどのように動いているかを理解していれば,先に述べたようにフレームワークによる記述方法の差は小さいと思います.
研究開発のスピードが非常に速い分野ですので,1つのライブラリーに注力しすぎるのは危険な気もします.ひょっとすると数年後にはJuliaとMXNetを使うのが主流になっているかもしれません.AutoMLのようなものも今後どんどん進歩していくでしょうから,フレームワークの使い方を単に覚えるだけの学習は辞めて,もっと普遍的・本質的な理解を目指して学習していくのが望ましいでしょう.
本ブログではTensorflow/Kerasで深層学習の基本を押さえた上で,徐々にPyTorchへ移行しながら論文などをフォローしていく方針でいきたいと思います.
Tensorflow2とKeras
Kerasとは
KerasはGoogleのFrançois Cholletにより作成されたオープンソースの深層学習用ライブラリです.少ないコードで,素早く複雑なモデルを組み上げられるように設計されており,その使いやすさから多くのユーザーを獲得しました.もともと計算エンジンとしては
- TensorFlow
- CNTK
- Theano
など複数のフレームワークのいずれかを利用することを想定して作成されました.このようなマルチバックエンドをサポートしたKerasはversion 2.3をもって開発が終了しました.
tf.kerasとは
Tensorflowを用いてモデルを作成することに特化したKerasがtensorflow.kerasになります.これまでのKerasと同じように簡単にモデルが記述できるうえに,文字通りTensorflowに組み込まれているため,フレームワークに固有の機能と連携しやすいように機能拡張されています.
以下ではTensorflow2を用いて,簡単なネットワークから始めて少しずつ複雑な形へと展開していくことで,KerasのSequentialモデルの取り扱いに慣れていきます.
Sequentialモデルとは文字通り,いくつもの層が連続的に繋がった形のネットワークを作成するのに利用可能なモデルです.現実的には多くのネットワークがこの形式で記述できることから,Sequentialモデルに習熟することで世の中に出回っているコードのかなりの部分を読み解くことができるようになると思います.
ライブラリのインポートとデータの前処理
実際にニューラルネットワークのモデル作成に取りかかる前に必要なライブラリのインポートとデータの読み込みを行います.今回は「Tox21は米国の大規模毒性学プロジェクト:HTSによるアッセイ結果は機械学習コンペで用いられたデータセット」という記事で扱ったTox21データセットの中から酸化ストレス応答パスウェイとしてしられるARE産生系をデータにしてみます.なおデータはMoleculeNetに収載されているcsvファイルを利用します.
下記のコードでは,
- ライブラリのインポート
- csvファイルのpandasデータフレームへの読み込み
- データフレームへのRDKitのMOLオブジェクトの追加
- モデルへの入力ベクトルとして用いるフィンガープリントの計算
- AREアッセイの結果が収録されている分子のみを取得
- データを訓練用データとテスト用データに分割
という順番で処理をしています.
# 1. ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, DataStructs
from rdkit.Chem.Draw import IPythonConsole
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()
import tensorflow as tf
from tensorflow import keras
import sklearn
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from scipy.stats import reciprocal
print('rdkit version: ', rdBase.rdkitVersion)
print('tensorflow version: ', tf.__version__)
print('keras version: ', keras.__version__)
print('sci-kit learn version: ', sklearn.__version__)
# rdkit version: 2019.09.3
# tensorflow version: 2.0.0
# keras version: 2.2.4-tf
# sci-kit learn version: 0.21.2
# 2,3. Pandasデータフレームへの読み込みとMOLオブジェクト追加
df = pd.read_csv('./tox21.csv')
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='smiles')
# 4. フィンガープリントの計算
def fp2array(mol):
ar = np.zeros((1,2048))
fp = AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)
DataStructs.ConvertToNumpyArray(fp, ar)
return ar
df['fp'] = df.ROMol.map(fp2array)
# 5. 対象分子の絞り込み
print(len(df)) # 7831
print(df['SR-ARE'].isnull().sum()) # 1999
selected_index = df['SR-ARE'].dropna().index
input_fps = df.fp[selected_index]
input_fps = np.array(list(input_fps))
target = df['SR-ARE'][selected_index]
# 6. データセットの分割
np.random.seed(1234)
X_train_val, X_test, y_train_val, y_test = train_test_split(input_fps, target)
X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val)
print(X_train.shape, X_val.shape)
# ((3280, 2048), (1094, 2048))
pd.value_counts(target)
大体5800分子のうち,1/6程度が陽性のようです.
0.0 4890 1.0 942 Name: SR-ARE, dtype: int64
KerasのSequentialモデル
keras.models.Sequential().add(layer)
Kerasでは全結合層や活性化関数層など1つ1つのレイヤーを部品として扱い,それを連続的に繋げていきます.レイヤーの追加方法としては,
- Sequentialインスタンス作成時にレイヤーのリストを渡す方法
- addコマンドで逐次的にレイヤーを追加していく方法
があります.どちらも頻繁に使われます.
中間層のないシンプルなモデル
モデルの定義
keras.layers.Activation(function)
まずは中間層なしの,入力層と出力層のみから形成されるモデルをベンチマークとして作成してみましょう.今回は入力フィンガープリントが2048bitで,出力層は1次元です.また出力は0か1になりますので,活性化関数としてシグモイドを使います.
このモデルは以下のように記述できます.
model = keras.models.Sequential()
model.add(keras.layers.Dense(1, input_shape=[2048]))
model.add(keras.layers.Activation('sigmoid'))
活性化関数はDenseレイヤーに組み込むことができます.こちらの方がよく使われる書き方です.
model_simple = keras.models.Sequential()
model_simple.add(keras.layers.Dense(1, activation='sigmoid',
input_shape=[2048]))
model_simple.summary()
keras.utils.plot_model(model_simple)
summary関数を使うと,モデルの構成要素やパラメータ数などが確認できます.今回は入力層2048に対して重みがそれぞれ1つ存在し,さらにバイアスが1つありますので,合計で2049個のパラメータを有するモデルになります.
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 1) 2049 ================================================================= Total params: 2,049 Trainable params: 2,049 Non-trainable params: 0
またkeras.utils.plot_model関数を使うとモデルを以下のように可視化できます.
モデルのコンパイル
続いて作成したモデルについて,
- どの損失関数を用いるか(keras.losses)
- どの最適化手法を用いるか(keras.optimizers)
- どの評価関数を用いるか(keras.metrics)
などを決定します.この作業をKerasではモデルのコンパイルと呼びます.
以下ではそれぞれ
- バイナリ交差エントロピー
- 学習率10-4のAdam
- 精度
を指定しています.
model_simple.compile(loss=keras.losses.binary_crossentropy,
optimizer=keras.optimizers.Adam(lr=1e-4),
metrics=['acc'])
モデルの学習
モデルの学習にはfit関数を用います.fit関数は
- 学習データ
- 学習エポック数
- 評価用データ(または評価用データに用いる割合)
などを引数とします.1エポックとはモデルが訓練用データを一通り見た状態を言います.エポック数が多くなるほど,学習は進みますが過学習の危険性も向上します.
fit関数は学習記録を戻り値とします.これを見ることで学習がどのように進行したかを知ることができます.下のコードでは学習過程の損失関数と評価関数の推移を訓練用データと評価用データに分けてプロットしています.
history0 = model_simple.fit(X_train, y_train, epochs=50,
validation_data=[X_val, y_val])
def plot_history(history):
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
acc = history_dict['acc']
val_acc = history_dict['val_acc']
epochs = range(1, len(history_dict['acc']) + 1)
plt.figure(figsize=(12,5))
plt.subplot(121)
plt.plot(epochs[::5], loss_values[::5], 'o', alpha=0.7, label='training loss')
plt.plot(epochs, val_loss_values, label='validation loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.ylim(0,1)
plt.title('training vs validation')
plt.legend()
plt.subplot(122)
plt.plot(epochs[::5], acc[::5], 'o', alpha=0.7, label='training acc')
plt.plot(epochs, val_acc, label='validation acc')
plt.xlabel('epochs')
plt.ylabel('acc')
plt.ylim(0,1)
plt.legend()
return plt.show()
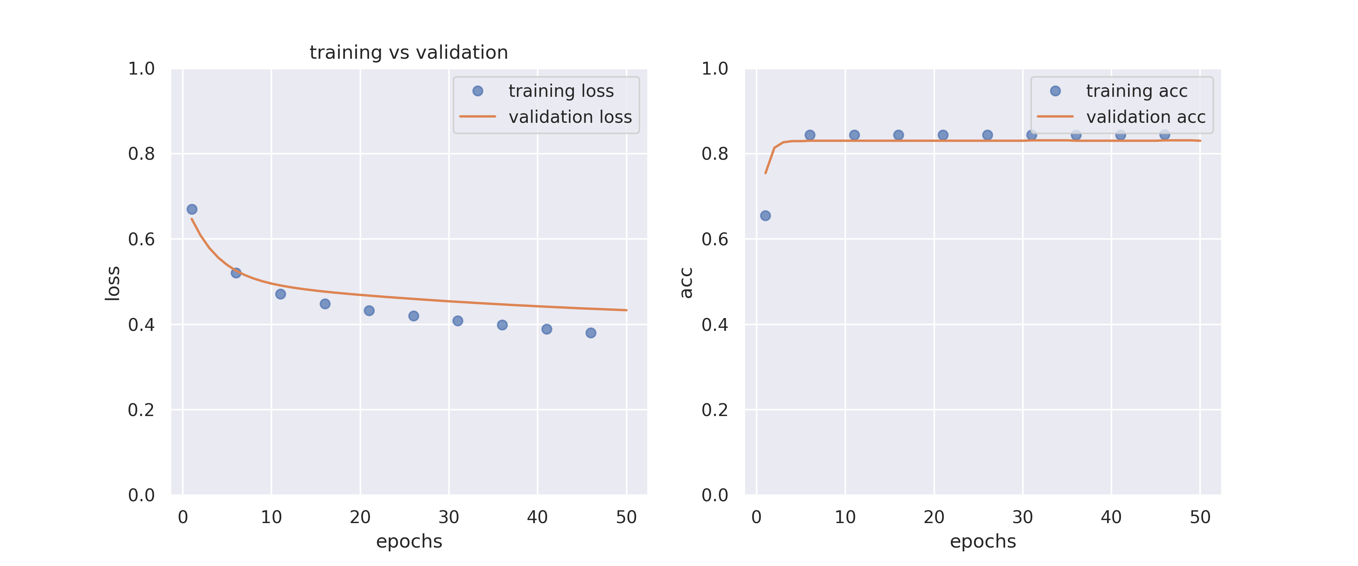
plot_history(history0)
学習が進むにつれて評価用データのlossが下がっていく様子が見てとれます.
中間層1のモデル
中間層を増やすことでモデルのパラメータ数が増え,それだけモデルが複雑化します.このため,モデルの表現力が向上しますが,同時に学習にも時間がかかります.また過学習の危険性も徐々に増えていきます.
先ほどのシンプルなモデルに中間層を1つ加えてみます.ここではニューロン10個からなる中間層を加えてみます.活性化関数は「ReLU」とします.
model1 = keras.models.Sequential([
keras.layers.Dense(10, activation='relu',
input_shape=[2048]),
keras.layers.Dense(1, activation='sigmoid')
])
model1.summary()
このモデルではパラメータ数は
- 最初の層:2048 x 10(重み) + 10(バイアス)
- 第2層:10 x 1(重み) + 1(バイアス)
であり,合計20501個になります.中間層の追加によりパラメータが大幅に増加したことが確認できます.
Model: "sequential_2" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_2 (Dense) (None, 10) 20490 _________________________________________________________________ dense_3 (Dense) (None, 1) 11 ================================================================= Total params: 20,501 Trainable params: 20,501 Non-trainable params: 0
モデルのコンパイル,学習は先ほどと同様です.
model1.compile(loss=keras.losses.binary_crossentropy,
optimizer=keras.optimizers.Adam(lr=1e-4),
metrics=['acc'])
history1 = model1.fit(X_train, y_train, epochs=50,
validation_data=[X_val, y_val])
plot_history(history1)
先ほどのモデルと比べると訓練データと評価用データの差が大きくなっています.学習後半では評価用データの値はほとんど向上していないようにも見えます.
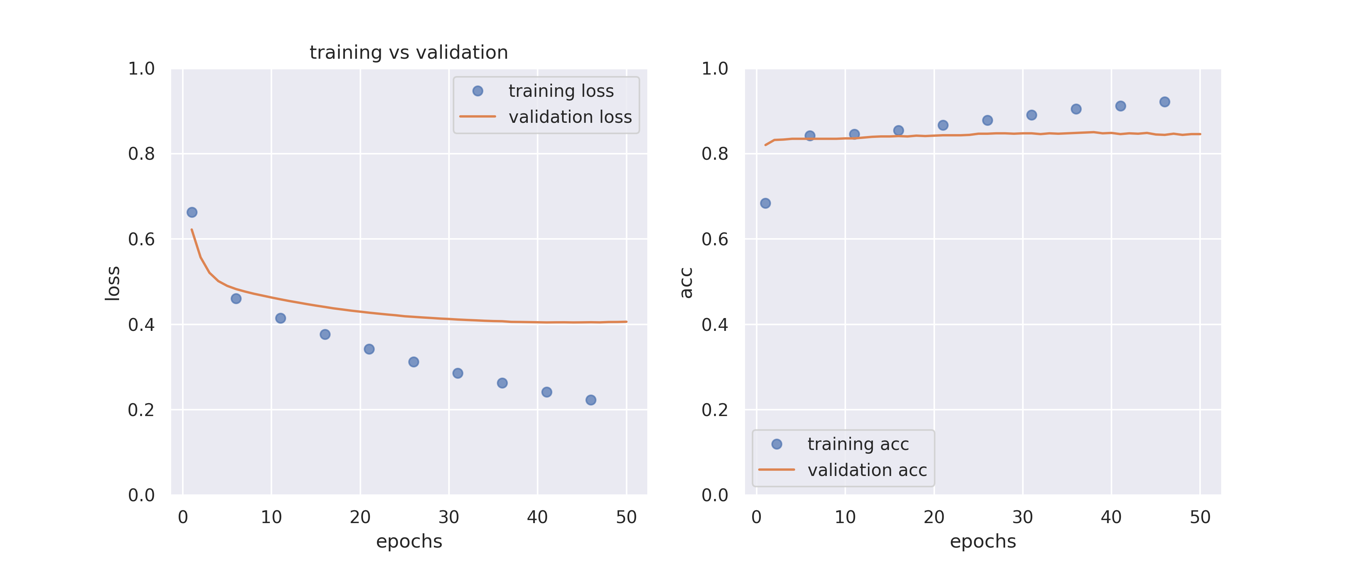
中間層3つのモデル
さらに中間層の数を増やし,各層ごとのニューロン数を100にしてみましょう.
model2 = keras.models.Sequential([
keras.layers.Dense(100, activation='relu',
input_shape=[2048]),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
model2.summary()
パラメータ数はさらに増え,225201個になりました.
Model: "sequential_3" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_4 (Dense) (None, 100) 204900 _________________________________________________________________ dense_5 (Dense) (None, 100) 10100 _________________________________________________________________ dense_6 (Dense) (None, 100) 10100 _________________________________________________________________ dense_7 (Dense) (None, 1) 101 ================================================================= Total params: 225,201 Trainable params: 225,201 Non-trainable params: 0
同様にコンパイルし,学習させてみます.モデルが複雑になったのでエポック数を100に増やしています.
model2.compile(loss=keras.losses.binary_crossentropy,
optimizer=keras.optimizers.Adam(lr=1e-4),
metrics=['acc'])
history2 = model2.fit(X_train, y_train, epochs=100,
validation_data=[X_val, y_val])
plot_history(history2)
モデルの複雑さを増したことで訓練用データのロスは0になりましたが,評価用データのロスが途中から増加しています.過学習の兆候です.
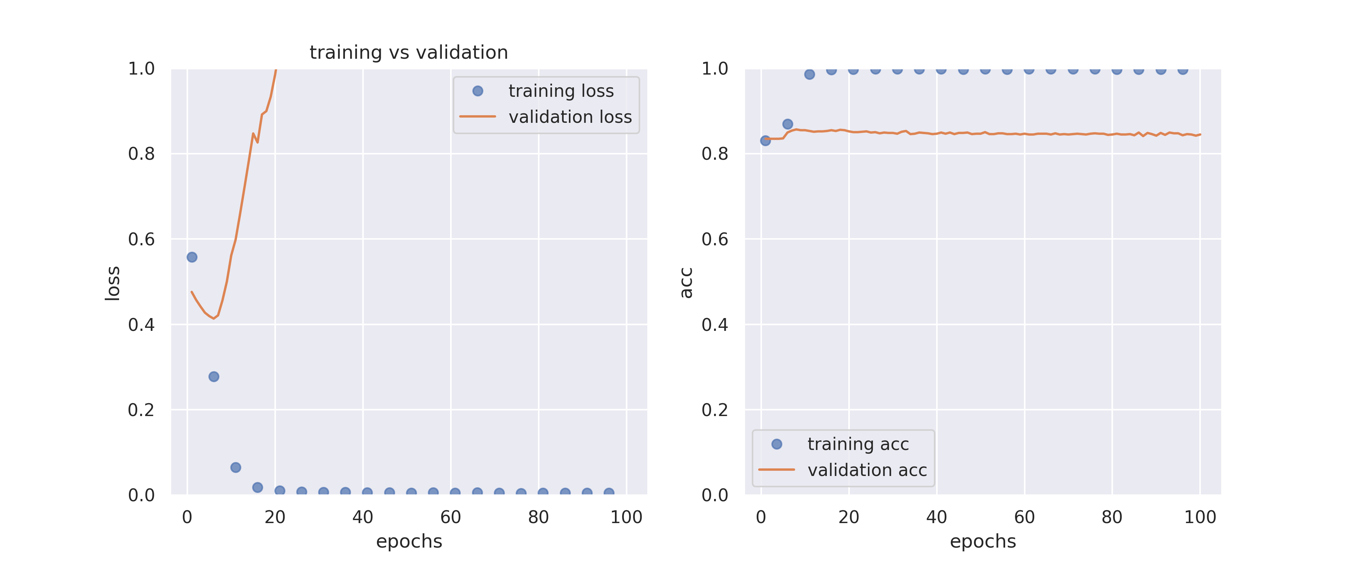
続いて,過学習を防ぐために正則化項の導入を行ってみましょう.
L2正則化の導入
「線形モデルを用いた化合物の溶解度予測:通常最小二乗法,Ridge回帰,Lasso回帰」という記事でもみたように,重みの大きさにペナルティを与えることで過学習を防ぐことができます.
KerasではL2正則化,L1正則化,そして2つを組み合わせたL12正則化(Elastic Net)がkernel_reguralizationパラメータを設定することで容易に利用可能です.
以下のコードでは,各全結合層にαの値を0.01にしてL2正則化を導入しています.
model3 = keras.models.Sequential([
keras.layers.Dense(100, kernel_regularizer=keras.regularizers.l2(0.01),
activation='relu', input_shape=[2048]),
keras.layers.Dense(100, kernel_regularizer=keras.regularizers.l2(0.01),
activation='relu'),
keras.layers.Dense(100, kernel_regularizer=keras.regularizers.l2(0.01),
activation='relu'),
keras.layers.Dense(1, kernel_regularizer=keras.regularizers.l2(0.01),
activation='sigmoid')
])
model3.compile(loss=keras.losses.binary_crossentropy,
optimizer=keras.optimizers.Adam(lr=1e-4),
metrics=['acc'])
history3 = model3.fit(X_train, y_train, epochs=100,
validation_data=[X_val, y_val])
plot_history(history3)
先ほどの場合と比べると大幅に過学習が抑制できていることがわかりますが,ロスも下がっていません.
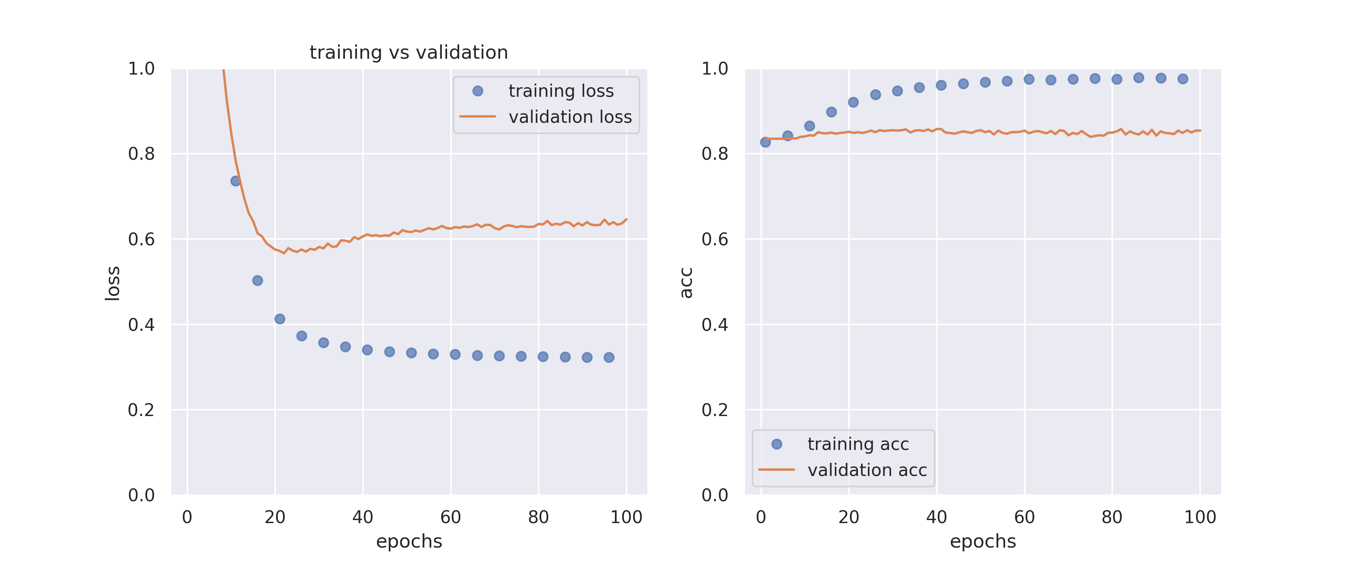
ドロップアウト層の追加
ドロップアウト層では,「全結合層を伝播する値をある確率で伝播させない(重みをゼロにする)」という処理を行います.これによって各ニューロンは近傍のニューロンに頼ることなく正確に予測を行う必要があり,精度向上が期待できるとされています.
ドロップアウトが適用されるのは訓練中のみで,評価の際には使われず十分に学習されたニューロンを利用することができます.keras.layersにDropout層が実装されていますので,これまで通りSequentialモデルに追加するだけで利用可能です.
下記コードでは各層について確率0.4でドロップアウトを適用しています.
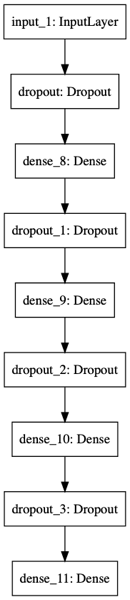
model4 = keras.models.Sequential([
keras.layers.Input(shape=[2048]),
keras.layers.Dropout(rate=0.4),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dropout(rate=0.4),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dropout(rate=0.4),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dropout(rate=0.4),
keras.layers.Dense(1, activation='sigmoid')
])
モデルの構成は以下の図のようになります.
model4.compile(loss=keras.losses.binary_crossentropy,
optimizer=keras.optimizers.Adam(lr=1e-4),
metrics=['acc'])
history4 = model4.fit(X_train, y_train, epochs=100,
validation_data=[X_val, y_val])
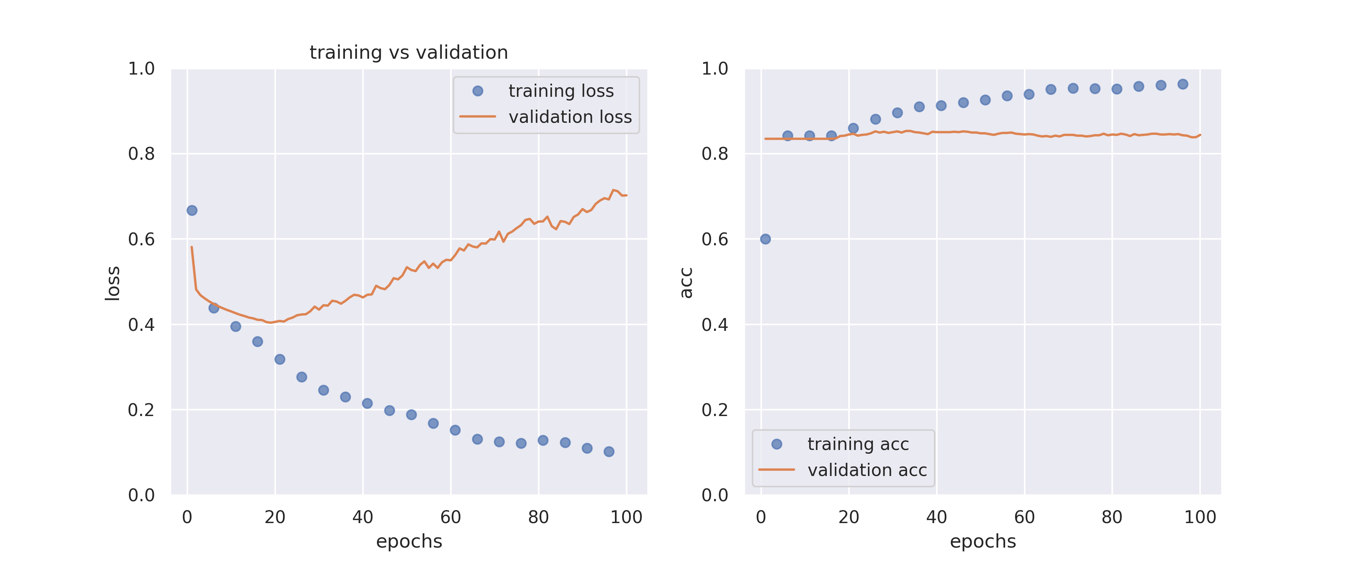
plot_history(history4)
L2正則化ほどではありませんが,過学習がある程度は抑制できています.
ハイパーパラメーター最適化
ここまでシンプルなモデルから始めて,
- 中間層の数を変更
- L2正則化の導入
- ドロップアウト層の追加
などによりモデルの構成を変えてきました.予測モデル作成に当たってはこれらの他にも
- 最適化手法の学習率
- 正則化項のα
- ドロップアウトの確率
などのハイパーパラメーターも変化させていき,ベストなモデルを構築していくことになります.すなわち「ハイパーパラメーター最適化」を行います.
「交差検証を用いてElastic Netを化合物の溶解度データに対して最適化」という記事では,何種類かのパラメータに対して総当たりでモデルを作成していく「グリッドサーチ」について説明しました.
今回はランダムにある範囲内のパラメータの組合せを試していく「ランダムサーチ」を用いて探索を行ってみます.
ランダムサーチ
keras.wrappers.scikit_learn.KerasClassifier(model-gen)
Kerasではscikit-learnのクロスバリデーションオブジェクトを利用しやすくなるsk-learn.wrapperクラスが実装されています.これを用いることで,scikit-learnのRandamizedCVオブジェクトにkerasのモデルを直接渡すことが可能になります.
以下のコードではKerasのモデルを作成する関数(build_model)を定義し,RandomizedSearchCVを用いて
- 中間層の数
- 中間層のニューロン数
- ドロップアウト率
- Adamの学習率
をスクリーニングしています.また場合によっては学習が遅い可能性を考えてエポック数を500に設定しています.この場合,早々に学習が終了してしまう場合を考え,「EarlyStopping」という検証用データのロスに変化が見られなくなった場合に学習を終了する設定を加えています.過学習を防ぐためにもEarlyStoppingは重要なテクニックになります.
クロスバリデーションオブジェクトに訓練用データと評価用データを渡していますが,実際にパラメータ探索に使われるのは訓練用データであり,評価用データはEarlyStopping評価のためだけに使われることに注意してください.
なお以下のコードはscikit-learn 0.22ではバグがあってうまく動きません.0.21を利用してください.
def build_model(n_hidden=1, n_neurons=10, dropout_rate=0.4, learning_rate=1e-4, input_shape=[2048]):
model_built = keras.models.Sequential()
model_built.add(keras.layers.InputLayer(input_shape=input_shape))
for i in range(n_hidden):
model_built.add(keras.layers.Dropout(rate=dropout_rate))
model_built.add(keras.layers.Dense(n_neurons,
activation='relu'))
model_built.add(keras.layers.Dropout(rate=dropout_rate))
model_built.add(keras.layers.Dense(1, activation='sigmoid'))
optimizer = keras.optimizers.Adam(lr=learning_rate)
model_built.compile(loss=keras.losses.binary_crossentropy,
optimizer=optimizer,
metrics=['acc'])
return model_built
keras_clf = keras.wrappers.scikit_learn.KerasClassifier(build_fn=build_model)
param_distribs = {
'n_hidden': [0, 1, 2, 3],
'n_neurons': [10, 30, 100],
'dropout_rate': [0, 0.2, 0.5],
'learning_rate': reciprocal(1e-6, 1e-3),
'epochs': [500]
}
rnd_search_cv = RandomizedSearchCV(estimator=keras_clf, param_distributions=param_distribs,
n_iter=20, cv=5)
result = rnd_search_cv.fit(X_train, y_train,
validation_data=[X_val, y_val],
callbacks=[keras.callbacks.EarlyStopping(patience=5)])
print(result.best_params_)
20回探索して最もよかったパラメータの組合せは以下でした.
{'dropout_rate': 0,
'epochs': 500,
'learning_rate': 0.0005112763661716788,
'n_hidden': 0,
'n_neurons': 100}
今回の場合は最初のシンプルなモデルからほとんどロスが変化していないことから,精度向上のためにはニューラルネットワークの構成をいじるよりも,分子の特徴量ベクトルをもっと工夫することが必要そうです.
ベイズ最適化を利用したハイパーパラメーター探索
深層学習においてハイパーパラメーターの最適化は複雑で,モデルの精度に直結する非常に重要なトピックです.
今回はランダムにパラメータの探索を行いましたが,理想的には完全にどの領域もランダムに探索するのではなく「筋の悪い」領域には早々に見切りをつけて,最適解がありそうな領域に注力して探索する方が望ましいです.
そこでベイズ最適化を利用したハイパーパラメーター探索が行われています.例えば以下のようなライブラリを利用することでパラメータ探索の効率化が行えます.
終わりに
今回は「化学系深層学習入門:Tensorflow2で始めるディープラーニング」という話題について,
- 化学とディープラーニングの歴史
- ニューラルネットワークの構成要素
- 深層学習とフレームワーク
- Tensorflow2/Kerasを用いたモデル作成の具体例
などを説明しました.
この記事では化合物のベクトル表現としてMorganフィンガープリントを利用して予測モデルを作成しましたが,化合物のグラフ表現をもっと活かした特徴量の作成方法も報告されています.
今回はKerasのSequentialモデルを用いて次々と層を重ねることでディープラーニングモデルが作成できることを学びました.次回はKerasのFunctional APIと呼ばれるものを用いることで,枝分かれ構造のあるネットワークなど,より複雑なネットワークの作成方法を学んでいきたいと思います.

コメント