BCUTは分子のグラフ構造を基にした2D記述子

「化合物の隣接行列，距離行列，Wiener指数：RDKitを用いたグラフの扱い方」という記事では，原子をノード，結合をエッジとみなしたグラフとして分子を考え，RDKitを用いたグラフの扱い方について説明しました．また分子のグラフ表現から得られる2D記述子についても触れました．

今回取り上げる「BCUT記述子」も分子のグラフ表現を基にした2D記述子になります．RDKitでは2020.03のアップデートから利用可能になりました．

BCUT記述子の歴史
RDKitによるBCUT記述子の実装
BCUTメソッドの実装
終わりに

BCUT記述子の歴史

ところでBCUTという文字列が何を意味しているかわかるでしょうか？

この4文字はそれぞれ，

B: Burden
C: CAS
UT: University of Texas

を指しており，記述子開発の歴史に関係しています．

この項はPearlmanらによる「Novel Software Tools for Chemical Diversity」という記事を参考にしています．

Burdenによる化合物ID

1989年の論文でBurdenは化合物にIDをつける新しい方法を提案し，このIDの大小を比較することで化合物間の類似度を見積もることができると提唱しました．

具体的には水素を除いた原子数からなるサイズの行列について，

対角成分には原子番号
原子間に結合を有する場合は結合の種類に応じた値，単結合（0.1）, 二重結合（0.2）, 三重結合（0.3）, 芳香族結合（0.15）
末端原子に相当する場合0.01を追加
非結合成分については0.001

というルールに基づいて作成した行列を考え，その固有値のうち小さい方から数個をその化合物のIDとしました．

非結合成分をゼロ以外に変えることが本質的に重要ですが，規格化定数を含めてその値は恣意的なものであり改良の余地があることをBurdenも認めています．

このIDを用いると例えば総数663個の炭素数12のアルカンでは，最小固有値を小数点以下7桁まで考慮することで固有のIDを得ることができたようです．

BurdenはこのID表記が化合物データベースに有用と考えたようですが，丁度フィンガープリントを用いた類似度検索が台頭してきた時期でもあったため，この方法はほとんど注目を集めなかったようです．

フィンガープリントを用いた分子類似性については，「RDKitでフィンガープリントを使った分子類似性の判定」という記事で解説しています．参照してみてください．

CASによる実証実験

その後，1993年にCASがBurdenの提案を60000化合物程度のデータベースを用いて評価しました．結果はフィンガープリントを用いた手法と比べると芳しくなかったようですが，「想像していた以上に健闘した」と評されました．

この結果を受けて，CASではBurdenの行列について対角成分の変更なども試みたようです．何れの場合も最小の固有値を用いた表記法を用いていました．

テキサス大学のチームによる拡張

テキサス大学のPearlmanらはBurdenとCASの結果をもとに，次のような拡張を行いました．

最小固有値に加えて最大固有値も利用する
対角成分として原子量に加えて電荷やlogPなど，他の値を利用する
結合情報を用いる部分はそのまま残す
もし3次元座標を用いてユークリッド距離を非対角成分にすれば立体情報を取り込める

特に最後の3次元座標を用いる拡張は「BCUT3D」などと呼ばれる記述子になります．

原子量以外の他の要素を取り入れた上で，多次元ベクトルとすることで表現力の向上した記述子になりました．

RDKitによるBCUT記述子の実装

Chem.rdMolDescriptors.BCUT2D(mol)
Chem.rdMolDescriptors.BCUT2D(mol, atom_props)
Chem.rdMolDescriptors.BCUT2D(mol, atom_propname)

rdMolDescriptors.BCUT2Dメソッドは特に何も指定しないと8つの値を含むタプルを返します．それぞれの値は

原子量
Gasteiger電荷
MolLogP
MolMR

を対角成分に使った値で

原子量の最大固有値
原子量の最小固有値
Gasteiger電荷の最大固有値
Gasteiger電荷の最小固有値
MolLogPの最大固有値
MolLogPの最小固有値
MolMRの最大固有値
MolMRの最小固有値

の順番に格納されています．

実際の実装としてはBurdenのオリジナル論文では「単結合（0.1）, 二重結合（0.2）, 三重結合（0.3）, 芳香族結合（0.15）」が規格化に用いられていましたが，RDKitではそれぞれ

$$ \frac{1}{\sqrt{結合タイプ}} $$

を用いて規格化しています．また末端構造への0.01の加算も行っていないようです．興味のある方はC++ソース中のコメントで確認してみてください．

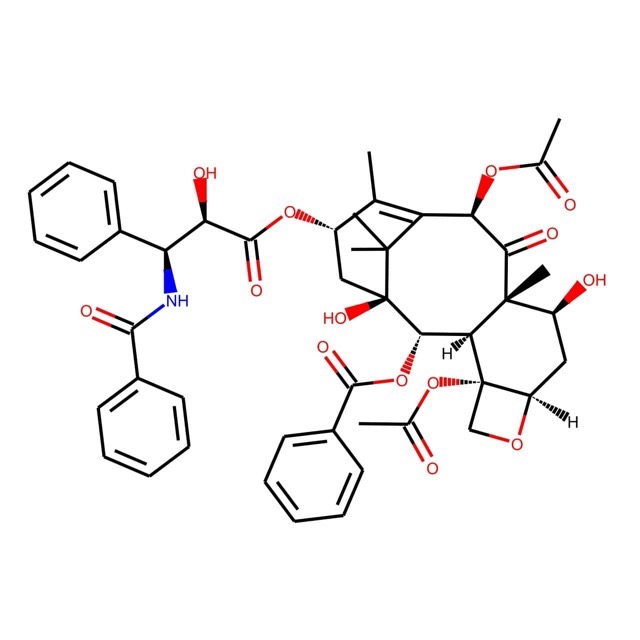
特に難しい点はないですが，下のコードではPubChemから得たタキソールのデータを例にBCUT2Dメソッドを使ってみています．

from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, rdMolDescriptors
print('rdkit version: ', rdBase.rdkitVersion)
# rdkit version:  2020.03.1

mol = Chem.MolFromSmiles('CC1=C2[C@H](C(=O)[C@@]3([C@H](C[C@@H]4[C@]([C@H]3[C@@H]([C@@](C2(C)C)(C[C@@H]1OC(=O)[C@@H]([C@H](C5=CC=CC=C5)NC(=O)C6=CC=CC=C6)O)O)OC(=O)C7=CC=CC=C7)(CO4)OC(=O)C)O)C)OC(=O)C')
print(tuple(rdMolDescriptors.BCUT2D(mol)))

前述の通り，8個の値が得られました．

(16.63726267137172, 9.44359263310062, 
2.780723982858056, -2.6703099251237656, 
2.641516956364917, -2.815220388494738, 
5.960987193723824, -0.3455531656402237)

またrdMolDescriptors.BCUT2Dメソッドは第２引数に原子毎の寄与を示すリスト・タプルを渡すことで，その値を用いて計算した2つの固有値を返します．

下のコードではMolLogPだけを指定しています．

crippen = rdMolDescriptors._CalcCrippenContribs(mol)
logp = [i for (i,j) in crippen]
print(rdMolDescriptors.BCUT2D(mol, logp))

当然ですが，先ほどの5,6番目と同じ値が得られています．

(2.641516956364917, -2.815220388494738)

同様の方法によって，例えば「計算化学における電荷：psi4を用いた電子密度解析」という記事で説明したMulliken電荷なども利用可能です．

BCUTメソッドの実装

最後に理解を深めるためにBCUTメソッドを原子量を例にして自分で実装してみます．

内容としてはnumpy.zerosで作成した行列に対して，

対角成分をAtom.GetMassで埋める
全ての結合に対して結合タイプを求めて（Bond.GetBondType），開始・終端原子をインデックスとして値を埋める
ここまでの時点で要素がゼロの部分を0.001に変更する
固有値を求めてソートする

という順番で作業しています．

import numpy as np
from numpy import linalg

def BCUT_2D_mass(m):
    n_atoms = m.GetNumAtoms()
    arr = np.zeros((n_atoms, n_atoms))
    
    for i, atom in enumerate(m.GetAtoms()):
        arr[i, i] = atom.GetMass()
    
    for bond in m.GetBonds():
        begin_id = bond.GetBeginAtomIdx()
        end_id = bond.GetEndAtomIdx()
        bond_type = bond.GetBondType()
        if str(bond_type) == 'SINGLE':
            value = 1 / (1 ** 0.5)
        elif str(bond_type) == 'DOUBLE':
            value = 1 / (2 ** 0.5)
        elif str(bond_type) == 'TRIPLE':
            value = 1 / (3 ** 0.5)
        elif str(bond_type) == 'AROMATIC':
            value = 1 / (1.5 ** 0.5)
        arr[begin_id, end_id] = value
        arr[end_id, begin_id] = value
    
    arr[arr == 0] = 0.001
    eigvals = linalg.eigvals(arr)
    eigvals = sorted(eigvals)
    return (eigvals[-1], eigvals[0])

BCUT_2D_mass(mol)

先ほどと同じ値が得られました．

(16.637262671371747, 9.443592633100625)

続いてRDKitにはないBCUT3D用のメソッドも作成してみます．規格化定数は適当に0.01としています．

対角成分は2Dの場合と同じで，原子間のユークリッド距離の部分は「クーロン行列は分子の回転・並進操作に不変な化合物の表現法」記事で実装したものと同様のロジックで原子毎の距離を求めています．

def BCUT_3D_mass(m):
    n_atoms = m.GetNumAtoms()
    conf = m.GetConformer(-1)
    arr = np.zeros((n_atoms, n_atoms))
    
    for i, atom in enumerate(m.GetAtoms()):
        arr[i, i] = atom.GetMass()
        
    for i in range(n_atoms):
        for j in range(i, n_atoms):
            position1 = np.array(conf.GetAtomPosition(i))
            position2 = np.array(conf.GetAtomPosition(j))
            dist = np.sqrt(np.sum((position1 - position2) ** 2))
            arr[i, j] = dist * 0.01
            arr[j, i] = dist * 0.01
            
    eigvals = linalg.eigvals(arr)
    eigvals = sorted(eigvals)
    return (eigvals[-1], eigvals[0])


Chem.AddHs(mol)
AllChem.EmbedMolecule(mol, AllChem.ETKDGv3())
Chem.RemoveHs(mol)
print(BCUT_3D_mass(mol))