分子の構造を入力として,反応の選択性や生理活性など何らかの現象を出力とする予測モデルの作成はケモインフォマティクスにおける重要課題です.モデルの入力としては,分子の性質を表現する「記述子」がよく用いられ,
- 分子量やlogPなどの分子全体の特徴を表現する記述子
- ある部分構造の電子的・立体的な特徴を表現する記述子
に大きくわけられます.特に活性発現に重要な部分が判明している場合に,その部分構造の特徴の差異をモデルに組み込むことが予測精度の向上に大きく貢献することは容易に理解できると思います.
今回は,部分構造の立体的な特徴を記述する記述子として「Sterimolパラメータ」を紹介します.置換基の大きさを3つのパラメータで表現することでより精細な表現が可能となっている記述子です.
古典的な立体因子の記述子
Sterimolを紹介する前に,他の立体因子を表す記述子・パラメータについて,いくつか軽く触れます.
A-Value
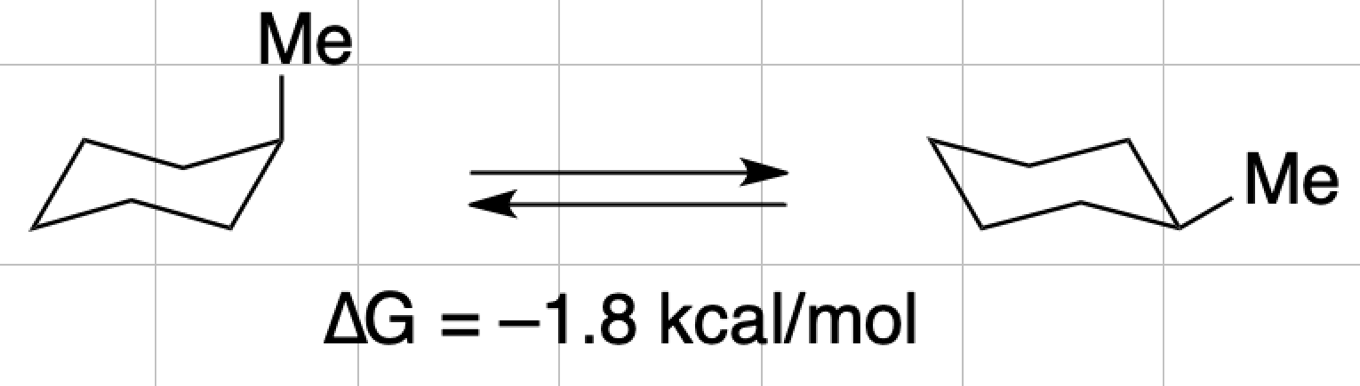
シクロヘキサンの配座解析に関する研究はよくなされており,最も安定な配座は「いす形」と呼ばれる配座になります.いす形配座の反転は炭素–炭素結合の回転を伴って起こります.シクロヘキサン環に置換基を導入した場合,反転エネルギーにはあまり影響を与えませんが,非等価になった2つのいす形配座間のエネルギー差には大きく影響します.
あるいす形配座でaxialに位置する置換基は,反転したもう一つのいす形配座ではequatorialに位置します.例えばメチルシクロヘキサンでは配座間のエネルギー差は1.8 kcal/mol程度であり,95%はequiatorial配置として存在しています.このようなエネルギー差を低温NMRなどの実験的手法により求めた値をA-Valueと呼んでいます.
以下にWikipediaよりいくつか代表的な値を抜粋します.
| 置換基 | A-Value |
|---|---|
| F | 0.15 |
| Cl | 0.43 |
| OCH3 | 0.6 |
| CH3 | 1.7 |
| CF3 | 2.1 |
| CH(CH3)2 | 2.15 |
| c-C6H11 | 2.15 |
| Ph | 3 |
| C(CH3)3 | >4 |
<引用元:A value(Wikipedia)>
例えば2つの置換基がシクロヘキサン上に存在する場合,A-Valueの大きい置換基の方がequatorial位に位置するような配座がより安定になると考えられます.このように置換シクロヘキサンの文脈で開発されたA-Valueですが,より一般的に「置換基の大きさを表す指標」として広く受け入れられています.
Taft–Chartonパラメータ
脂肪族エステルの酸加水分解では置換基の電子的効果が小さく,反応速度は置換基の立体因子で決まると考えられます.この仮定を利用し,様々なメチルエステルの酸加水分解速度の酢酸エステルに対する比を集めたものをTaft値といいます.

Taftのオリジナルの実験値をもとに様々な改良版が報告されています.Chartonは,Taftの実験値と計算により求めたvan der Waals半径とによい一致があることに気付き,実験値がない置換基についても計算によって推定することを可能としました.このTaft–ChartonパラメータはQSARモデルでよく使われています.
Sterimolパラメータ
Sterimolパラメータは1970年代にVerloopらが考案した一連のパラメータです.A-ValueやTaft–Chartonパラメータでは立体因子を1つの値で表していましたが,Sterimolパラメータでは3つの値で表現するため,より柔軟に立体因子を表現可能になっています.
具体的には下の図のように着目する置換基を結合方面から眺めた際に,置換基の幅が最も小さい部分(B1)と長い部分(B5)をパラメータとします.
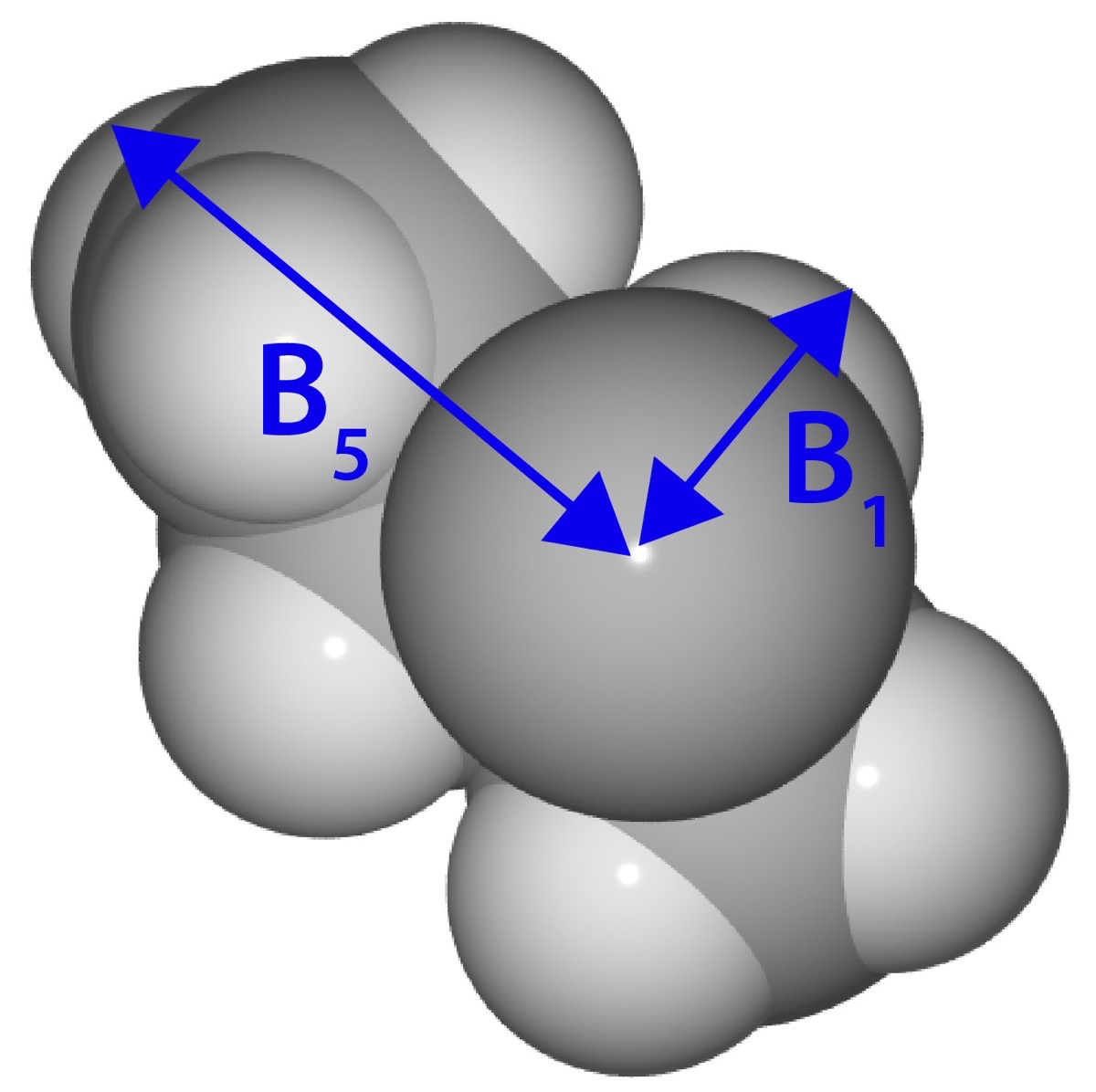
また横から眺めた際の置換基の奥行き(L)もパラメータとします.
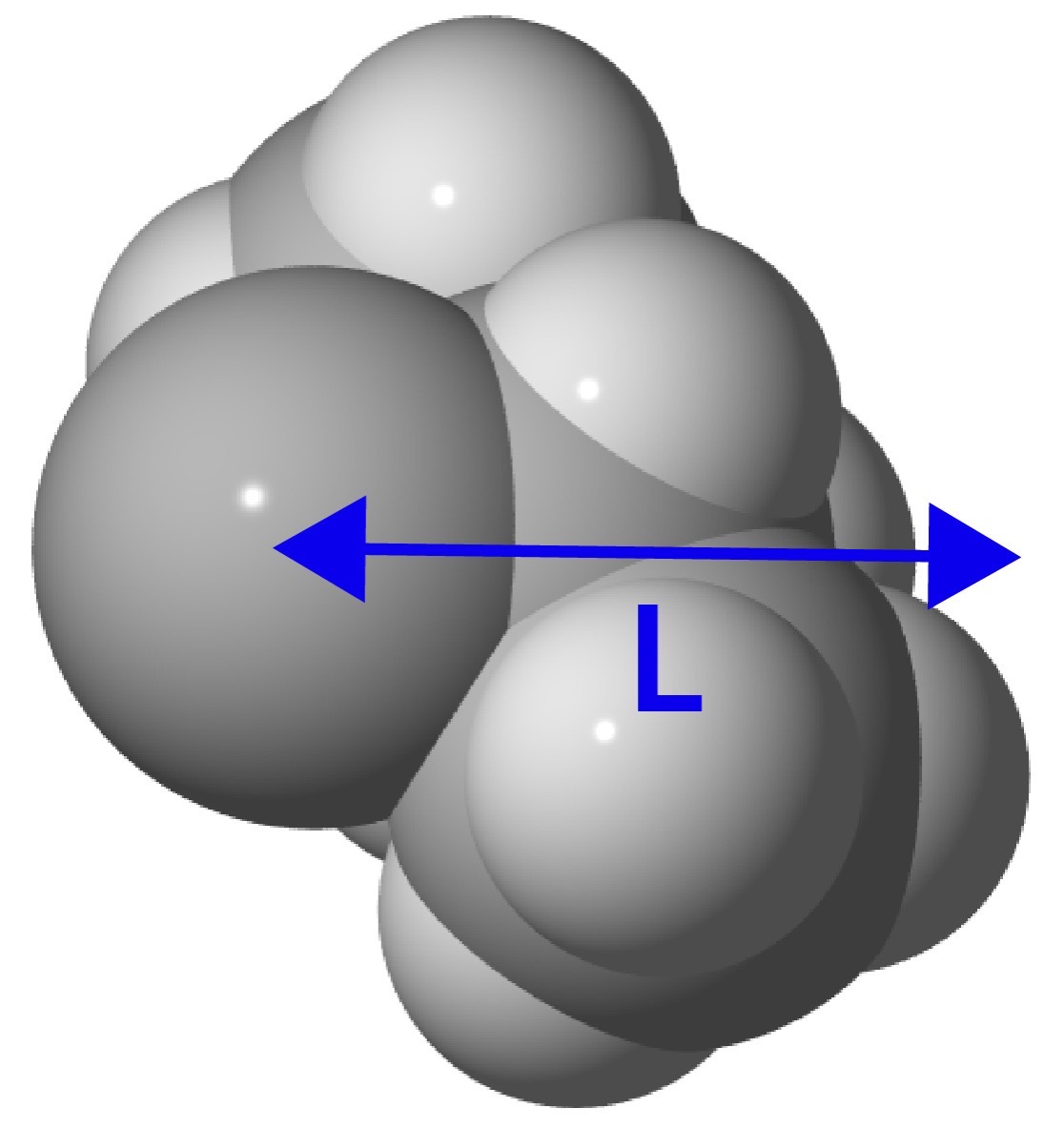
このような3つのパラメータを取ることで,特に非対称な置換基の形をより精細に表現可能になります.
Sterimolパラメータ自体は1970年代よりQSARの文献では使われていたようですが,有機化学反応の解析に持ち込まれたのはSigmanが不斉触媒反応のモデル化に用いるようになった2012年以降のことです.
Sterimolパラメータの利点として,マルチパラメータによる表現力の向上以外にも,A-ValueやTaft–Chartonパラメータのように実験値から値を取得する必要がないことが挙げられます.特に近年では計算化学ソフトの発達と計算機資源の増加が著しいことから,実験値が知られていない置換基についても容易に計算可能な点は大きな利点と言えます.
・ “Multidimensional steric parameters in the analysis of asymmetric catalytic reactions” Nature Chem. 2012, 4, 366–374.
・ “Prediction of Catalyst and Substrate Performance in the Enantioselective Propargylation of Aliphatic Ketones by a Multidimensional Model of Steric Effects” J. Am. Chem. Soc. 2013, 135, 2482-2485.
置換基のコンフォマー分布とwSterimolパラメータ
Sterimolパラメータは特に置換基が非対称な場合などに効果的ですが,一般にこのような置換基の多くは複数のコンフォメーションを取ります.それではどのコンフォメーションでSterimolパラメータを計算するのがよいでしょうか?
先ほどのSimgmanの例では最安定配座を基にSterimolパラメータを算出しています.不斉反応で用いられる基質や配位子の多くは対称性が高いことも多いこともあり,問題なく高精度のモデルが得られたようです.
しかし長鎖アルキル直鎖などを多く含むデータセットでは,エネルギーの近いながらも構造の大きく異なる配座が複数存在することから様相が異なることが予期できます.このような場合にも対応できるように,Boltzmann分布を加味したパラメータ化を行おうと提唱したのが最近オックスフォードからコロラド州立大学に移ったRobert Patonです.彼らはweighted Sterimol (wSterimol)と呼んでいます.
“Developing a Predictive Solubility Model for Monomeric and Oligomeric Cyclopropenium-Based Flow Battery Catholytes” J. Am. Chem. Soc. 2019, 141, 10171–10176.
wSterimolスクリプト
PatonらはPyMolから容易に利用可能なwSterimolを算出するスクリプトをgithubで公開しています.
具体的な使い方はgithubのページを見て頂きたいのですが,簡単な流れとしては
- PDBファイルを入力として準備
- PyMolコンソールでスキャンしたい二面角のリストを入力
- スクリプトが二面角をスキャンしながらコンフォマーを生成,バックエンドの構造最適化計算用の入力ファイルを作成
- コンフォマー毎に構造最適化計算
- 同一構造に収束した構造を除去するなど後処理
- B1, B5, LのSterimolパラメータを各コンフォマー毎に計算
- Boltzmann分布に応じてwSterimolを計算
となっています.
構造最適化としてはGaussian(M06-2X-D3/6-31G(d))とMopac(PM7)が選択できますが,自分で他の計算ソフト用の入力ファイルを作成するように書き直すのも比較的容易かと思います(スクリプトはMITライセンスです).なお計算レベルは設定ファイルで変更可能になっています.
また代表的な置換基のwSterimol値(M06-2X/6-311+G(d,p)//M06-2X/6-31G(d)レベルの計算値)は下記論文の実験項Table S2にまとめられていますので,そのまま利用可能になっています.
“Conformational Effects on Physical-Organic Descriptors: The Case of Sterimol Steric Parameters” ACS Catal. 2019, 9, 2313-2323.
wSterimolを用いた線形モデルの構築
ここではwSterimol論文の実験項TableS4に記載のデータを用いて,下記のMillerによって開発されたビスフェノールの不斉非対称化反応の不斉収率を予測するモデルを作成してみます.Sigmanらが既にこの反応は置換基RのB1とLが重要という知見を得ていますので,今回はそれを使います.

モデル作成には以下の12個基質の結果を用います.実験結果のeeを∆∆G‡に変換してあり,この値を予測するモデルを作成します.
| Groups | ∆∆G‡ | wB1 | wB5 | wL |
|---|---|---|---|---|
| Me | 0.543 | 1.51 | 2.02 | 2.98 |
| Et | 0.603 | 1.56 | 3.16 | 4.15 |
| Ph | 0.511 | 1.7 | 3.15 | 6.37 |
| Bn | 0.4385 | 1.57 | 6 | 5.43 |
| iPr | 0.8845 | 1.92 | 3.18 | 4.12 |
| tBu | 1.724 | 2.76 | 3.18 | 4.09 |
| Cy | 0.722 | 1.93 | 3.53 | 6.19 |
| CH2tBu | 0.582 | 1.56 | 4.45 | 5.09 |
| CHEt2 | 1.1195 | 2.01 | 4.45 | 4.54 |
| CH2iPr | 0.3495 | 1.56 | 4.44 | 4.79 |
| CHPh2 | 0.817 | 1.98 | 6.12 | 5.85 |
| Ad | 1.7055 | 3.17 | 3.51 | 6.19 |
標準化しないデータを用いたモデル作成:Sigmanモデルの再現
SigmanはMATLABを用いてモデリングを行っていますが,ここではpythonのstatsmodelsを用いていきます.
Sterimolの3つのパラメータを利用したモデル
まずはwSterimolのwB1, wB5, wLの全てを用いてモデルを作成してみます.
## ライブラリのインポート
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
## データフレームの作成
col = ['ddG','wB1','wB5','wL']
df = pd.DataFrame({'Me': [0.543,1.51,2.02,2.98],
'Et': [0.603,1.56,3.16,4.15],
'Ph': [0.511,1.7,3.15,6.37],
'Bn': [0.4385,1.57,6,5.43],
'iPr': [0.8845,1.92,3.18,4.12],
'tBu': [1.724,2.76,3.18,4.09],
'Cy': [0.722,1.93,3.53,6.19],
'CH2tBu': [0.582,1.56,4.45,5.09],
'CHEt2': [1.1195,2.01,4.45,4.54],
'CH2iPr': [0.3495,1.56,4.44,4.79],
'CHPh2': [0.817,1.98,6.12,5.85],
'Ad': [1.7055,3.17,3.51,6.19]})
df = df.T
df.columns = col
## モデル作成と結果の表示
full_model = smf.ols('ddG ~ wB1 + wB5 + wL', data=df).fit()
print(full_model.summary().tables[1])
wB5のP値が0.57と高く,Sigmanが得た知見通りにモデルには必要なさそうなことが確認できました.
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.4598 0.193 -2.384 0.044 -0.905 -0.015
wB1 0.9010 0.067 13.382 0.000 0.746 1.056
wB5 0.0179 0.031 0.570 0.584 -0.055 0.090
wL -0.1047 0.037 -2.837 0.022 -0.190 -0.020
==============================================================================
2つのパラメータを利用したモデル
続いてwB1とwLだけを用いてモデルを作成してみます.
partial_model = smf.ols('ddG ~ wB1 + wL', data=df).fit()
print(partial_model.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.4213 0.174 -2.424 0.038 -0.815 -0.028
wB1 0.8908 0.062 14.261 0.000 0.750 1.032
wL -0.0943 0.031 -3.053 0.014 -0.164 -0.024
==============================================================================
以下のようにSigmanがB1とLを用いて得た式とほぼ同様のものが得られました.
$$ ∆∆G^{‡}_{Sigman} = -0.418 + 0.929B_1 – 0.109L $$
$$ ∆∆G^{‡}_{wSterimol} = -0.421 + 0.891wB_1 – 0.094wL $$
スケール化したデータを用いたモデル作成:Patonモデルの再現
wSterimolの論文でPatonはデータを標準化(平均0,分散1)にしてから,R言語を用いてモデルを作成しています.
scikit-learnのStandardScalerでも標準化できますが,こちらを用いると標準偏差を求める際に標本標準偏差を利用します(自由度0).一方でR言語で標準化する場合には不偏標準偏差(自由度1)を用います.今回はPatonの結果を再現するために,StandardScalerを用いずに下記の式をもとに自分で標準化することとします.ddof=1とすることで不偏標準偏差で割っています.
$$ 標準化データ = \frac{データ – 平均値}{標準偏差} $$
## データの標準化
data = np.array(df)
data_scaled = (data[:,1:] - np.mean(data[:,1:], axis=0))/np.std(data[:,1:], axis=0, ddof=1)
df_scaled = pd.DataFrame(np.hstack((df.ddG.reshape(12,1), data_scaled)), columns=['ddG', 'wB1', 'wB5', 'wL'])
## モデル作成
scaled_model = smf.ols('ddG ~ wB1 + wL', data=df_scaled).fit()
print(scaled_model.rsquared.round(3))
print(scaled_model.summary().tables[1])
論文SIの22ページの結果と同じ値が得られました.
0.958
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.8333 0.030 27.479 0.000 0.765 0.902
wB1 0.4656 0.033 14.261 0.000 0.392 0.539
wL -0.0997 0.033 -3.053 0.014 -0.174 -0.026
==============================================================================
PatonらはタイプIの分散分析も行っていますので,こちらもstasmodelsで実施してみます.
import statsmodels.api as sm print(sm.stats.anova_lm(scaled_model, typ=1))
論文SIの22ページにある結果と同じテーブルが得られました.
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| wB1 | 1.0 | 2.143389 | 2.143389 | 194.233143 | 2.132638e-07 |
| wL | 1.0 | 0.102830 | 0.102830 | 9.318398 | 1.373490e-02 |
| Residual | 9.0 | 0.099316 | 0.011035 | NaN | NaN |
終わりに
今回の記事では「QSARにおける立体因子の記述:Sterimolパラメータを用いた線形モデル」という内容について,
- 代表的な立体因子の種類
- Sterimolパラメータとは何か
- Boltzmann分布を加味したwSterimolパラメータ
- Statsmoldesを用いた線形モデルの構築
などについて扱いました.
Taft–Chartonパラメータは反応速度をもとに算出していますので,反応系における置換基のアンサンブル効果を取り込んでいると考えることもできます.しかし置換基の「長さ」のみを別個にパラメータ化したSterimolの方がよい結果を与えることもあるという事実は,興味深いと思います.
今回取り上げた立体因子は主に「立体障害(Pauli反発)」であると考えられます.有機反応の予測モデル作成の研究では,他の立体因子として分散力のようなattractiveな相互作用を評価する記述子も開発されていますので,今後取り上げていきたいと思います.
コメント