計算化学における電荷：psi4を用いた電子密度解析

「計算手法とエネルギー・最適化構造の関係：コンフォメーション探索における注意点」という記事では，psi4を用いて様々な計算手法を用いてエネルギー計算を行うことで，

• 計算手法によって考慮できる相互作用が異なる

ことを説明しました．その結果

• 構造最適化できないことがある
• コンフォマー間のエネルギー差が逆転する場合がある

ことなどを具体例を通して見てきました．

ところで，エネルギー計算により得られるのは分子のエネルギーだけではありません．今回はシュレディンガー方程式の解である波動関数から得られる，様々な情報について見ていきたいと思います．

今回も量子化学計算のエンジンとしてpsi4を用いています．本ブログではpsi4を用いたエネルギーと構造最適化の基本について「計算化学にpythonとpsi4で入門」や「計算化学の構造最適化の基本をpsi4で学ぶ」という記事で解説しています．適宜参照してみてください．

計算化学にpythonとpsi4で入門

近年のコンピューターの高速化に伴い，実験化学者であっても高度な計算を手元の計算機で実行可能な環境が整いつつあります．計算化学とは「コンピュータを使って化学の問題を解く」学問領域で，分子力学法（MM）分子軌道法（MO）密度汎関数...

future-chem.com

2022.12.17

計算化学の構造最適化の基本をpsi4で学ぶ

「計算化学にpythonとpsi4で入門」という記事ではpythonで扱える量子化学計算ソフトウェア「psi4」の紹介と，簡単なエネルギー計算のやり方を扱いました．その際に得られるエネルギーは用いる計算レベルによってエネルギーの値...

future-chem.com

2022.12.11

電子密度解析とは何か

有機化学反応の多くは，「カチオン」と「アニオン」，「正電荷」と「負電荷」によって理解されています．例えばカルボニル基の求電子性は「C=O」の結合の電荷の偏りによって説明されます．

このような形式的な「電荷」を，波動関数の絶対値の二乗として得られる電子密度を用いて各原子に割り当てることを密度解析（population analysis）といいます．

割り当てるルールによっていくつかの方法が知られていますが，よく用いられるのは

• Mulliken（マリケン）密度解析
• Löwdin（ローディン）密度解析

の2つで，どちらもpsi4で利用可能です．

他の電荷としては

• 自然密度解析（NPA）

や静電ポテンシャルへのフィッティングによって電荷を決める

• Merz–Kollman電荷

などが有名です．

Mulliken電荷とLöwdin電荷

イオン結合性化合物の場合に，Mulliken電荷の方がよい結果を与えることが知られています．一方で，共有結合性化合物ではどちらもあまり変わらないことから，一般的にはMulliken電荷が用いられています．

とはいえ，先ほど述べたように電荷とは観測できない概念的なものですので，興味のある化合物群で傾向を見て判断するのが重要です．

それではpsi4とRDKitを用いて計算を行っていきましょう．まずは必要なライブラリーをimportしておきます．またSMILESを用いてRDKitのMolオブジェクトを生成し，xyz形式へと書き出す関数smi2xyzを定義しておきます．

## ライブラリのインポート
import psi4
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import time

from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools
from rdkit.Chem.Draw import IPythonConsole

print('rdkit version: ', rdBase.rdkitVersion) # rdkit version:  2019.09.3
print('psi4 version: ', psi4.__version__) # psi4 version:  1.3.2
print('numpy version: ', np.__version__) # numpy version:  1.17.4

## SMILESをxyz形式に変換
def smi2xyz(smiles):
    mol = Chem.AddHs(Chem.MolFromSmiles(smiles))
    AllChem.EmbedMolecule(mol, AllChem.ETKDGv2())
    AllChem.UFFOptimizeMolecule(mol)
    conf = mol.GetConformer(-1)
    
    xyz = '0 1'
    for atom, (x,y,z) in zip(mol.GetAtoms(), conf.GetPositions()):
        xyz += '\n'
        xyz += '{}\t{}\t{}\t{}'.format(atom.GetSymbol(), x, y, z)
        
    return xyz

## psi4の設定：各自の環境に合わせてください
psi4.set_num_threads(4)
psi4.set_memory('10GB')

Mulliken電荷

エネルギー計算や構造最適化計算における戻り値は通常エネルギーのみですが，return_wfnオプションをTrueにすることでWavefunctionオブジェクトが得られます．

波動関数の解析にはpsi4.oeprop（One-Electron properties）を用います．解析を行うと，Wavefunctionオブジェクトの所定のメソッドによって計算結果がアクセス可能になります．

Mulliken電荷の問題点

Mulliken密度解析では基底関数系にSTO-3Gなどの最小基底系を利用することを想定しています．そのため，大きな基底関数系を用いた場合には正しくない電荷分布が得られることがあります．このような基底関数系による一貫性の無さがMulliken電荷の問題点として広く認識されています．

以下のコードでは塩化メチルについて，基底関数系の大きさを変えていくことでMulliken電荷がどのように変化していくかを見ていきます．

MeCl = psi4.geometry(smi2xyz('CCl'))
basis_set = ['sto-3g', '3-21G', '6-31G(d)', '6-31+G(d,p)', '6-311++G(2d,p)']

import pandas as pd
df = pd.DataFrame()

psi4.set_output_file('MeCl.txt')
psi4.optimize('hf/sto-3g', molecule=MeCl)
for basis in basis_set:
    _, wfn_cl = psi4.energy('hf/' + basis, molecule=MeCl, return_wfn=True)
    psi4.oeprop(wfn_cl, 'MULLIKEN_CHARGES')
    df['hf/'+basis] = np.array(wfn_cl.atomic_point_charges())

df.index = ['C', 'Cl', 'H', 'H', 'H']

結果は以下の表のようになりました．電気陰性度から考えると炭素の方が塩素よりもポジティブになりそうですが，多くの場合に塩素原子の方がポジティブになっていることがわかります．

Löwdin電荷

Löwdin電荷についても同様にpsi4.oepropを用いて求めることができます．

Mulliken電荷をRDKitの類似度マップで可視化

「RDKitの類似度マップを用いて原子ごとの寄与を可視化する」という記事でGasteiger電荷について行った電荷マップの可視化をMulliken電荷でも行ってみます．

分子にはアスピリンを用いることとし，HF/STO-3Gで計算します．

## 分子の構築
psi4.set_output_file('aspirin.txt')
aspirin = psi4.geometry(smi2xyz('CC(OC1=C(C(=O)O)C=CC=C1)=O CC(=O)OC1C=CC=CC=1C(O)=O'))
_, wfn_asp = psi4.optimize('hf/sto-3g', molecule=aspirin, return_wfn=True)
rdkit_aspirin = Chem.AddHs(Chem.MolFromSmiles('CC(OC1=C(C(=O)O)C=CC=C1)=O CC(=O)OC1C=CC=CC=1C(O)=O'))
## Mulliken電荷の計算
psi4.oeprop(wfn_asp, 'MULLIKEN_CHARGES')
mulliken = np.array(wfn_asp.atomic_point_charges())
## 類似度マップで可視化
from rdkit.Chem.Draw import SimilarityMaps
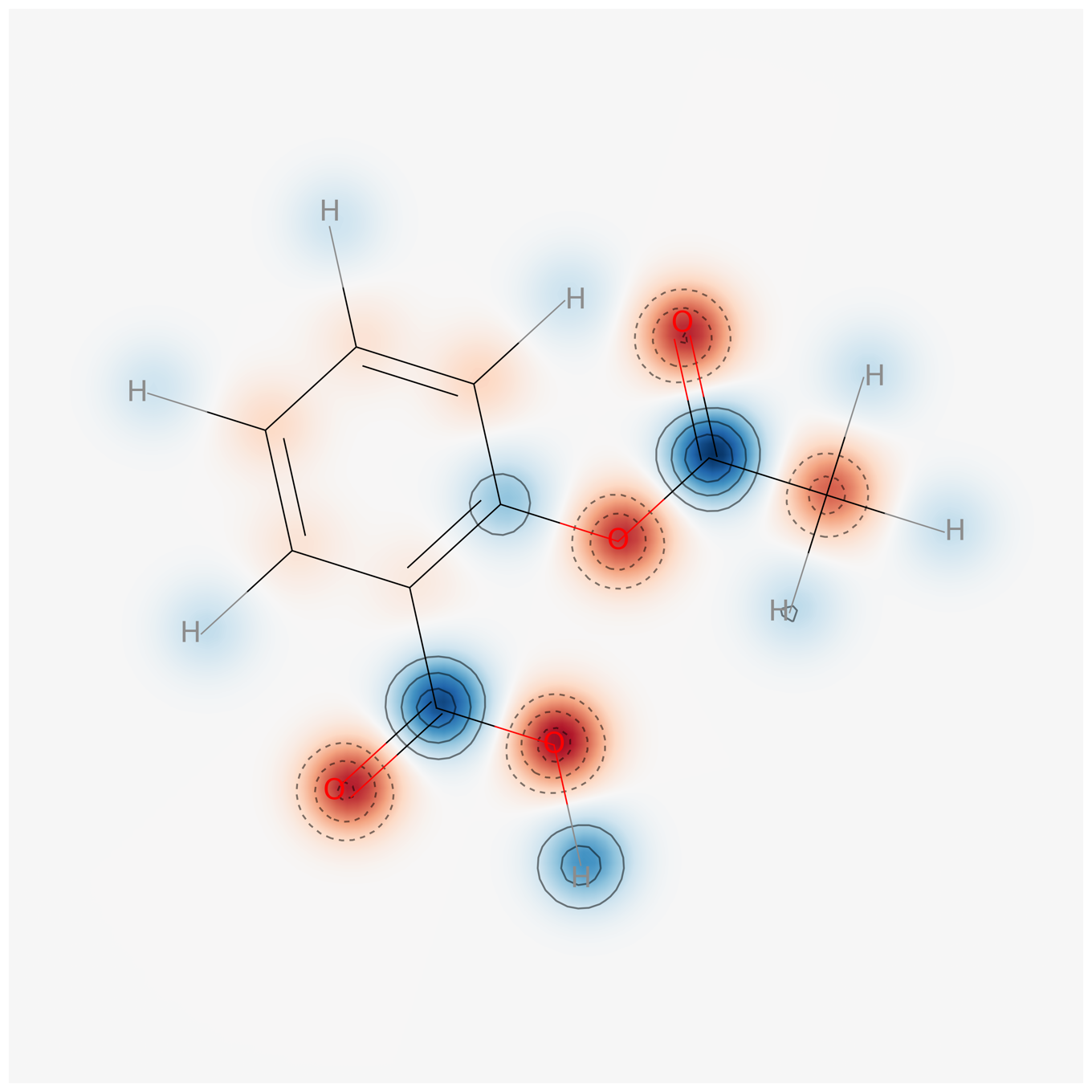
fig = SimilarityMaps.GetSimilarityMapFromWeights(rdkit_aspirin, mulliken, colorMap='RdBu')

青い部分が正電荷を帯びている部分になります．

双極子モーメント

双極子モーメントの各座標成分はpsi4.variableで取得可能です．双極子モーメントのXYZ成分がnumpy配列として取得できますので，分子全体の双極子モーメントの大きさを求めたい場合は自分でベクトルの大きさを計算する必要があります．

$$ dipole = \sqrt{x^2 + y^2 + z^2} $$

単位はデバイ（D, debye）です．

先ほどのアスピリンの双極子モーメントは1.41Dでした．

dipole_vec = psi4.variable('scf dipole')
dipole = np.sqrt(np.sum(dipole_vec ** 2))
print(f'{dipole:.3f}')
## 1.410

Wiberg結合次数

よく構造化学の分野の論文で使われているWiberg結合次数も求めることが可能です．ログファイル中に結合次数行列として出力されます．

以下の例ではスチレンを用いて，通常の二重結合と芳香族結合の結合次数が異なることを確かめてみましょう．

styrene = psi4.geometry(smi2xyz('C=Cc1ccccc1'))
psi4.set_output_file('Sty_Wiberg.txt')
_, wfn_sty = psi4.optimize('hf/sto-3g', molecule=styrene, return_wfn=True)
psi4.oeprop(wfn_sty, 'WIBERG_LOWDIN_INDICES')

出力は以下のように16原子 x 16原子の行列になります．下のログファイルで太字にしたように，

• 二重結合：1.95
• 芳香族結合：1.40

と違いが出ています．

Wiberg Bond Indices using Orthogonal Lowdin Orbitals:

  Irrep: 1 Size: 16 x 16

              1                   2                   3                   4                   5
    1     0.00000000000     1.95324109401     0.00073818541     0.03136594674     0.00033188156
    2     1.95324109401     0.00000000000     1.04581620233     0.00159509968     0.00630944500
    3     0.00073818541     1.04581620233     0.00000000000     1.40797156479     0.00079115441
    4     0.03136594674     0.00159509968     1.40797156479     0.00000000000     1.45142188611
    5     0.00033188156     0.00630944500     0.00079115441     1.45142188611     0.00000000000
    6     0.01628633247     0.00025892466     0.11073590864     0.00089592724     1.44069290921
    7     0.00020670447     0.00679507725     0.00085229099     0.11094786487     0.00093765801
    8     0.02894944073     0.00075567731     1.40471817351059     0.00090681862     0.11142786162
    9     0.98120867928     0.00023437704     0.00410605550     0.00011580928     0.00002081635
   10     0.98394387746     0.00036838891     0.00987370036     0.00034254791     0.00014266115
   11     0.00023335137     0.97589819640     0.00045570928     0.00167940083     0.00005966414
   12     0.00007998189     0.00268424198     0.00007474515     0.97872144722     0.00003084802
   13     0.00008273165     0.00049303434     0.00641896335     0.00002751182     0.98002610760
   14     0.00001230556     0.00008864824     0.00022518555     0.00636499688     0.00003852454
   15     0.00001742722     0.00050475695     0.00639030217     0.00022730512     0.00634128375
   16     0.00029904504     0.00283767782     0.00006327527     0.00634345703     0.00024429452
・・・省略・・・

終わりに

今回は「計算化学における電荷：psi4を用いた電子密度解析」という話題について，

• 電子密度解析とは何か
• Mulliken電荷とLöwdin電荷
• psi4を用いた密度解析のやりかた
• RDKitの類似度マップを用いた可視化
• 双極子モーメントの求め方
• Wiberg結合次数の求め方

などについて説明していきました．

今回取り扱った以外にもpsi4.Wavefunctionオブジェクトからは，HOMOやLUMOといった分子軌道に関する情報も取得可能で，外部プログラムと組み合わせることで軌道の可視化も可能になります．こちらについては，「psi4とCubeファイル：分子軌道や静電ポテンシャルマップの可視化」という記事で説明しています．

これまでエネルギー計算と構造最適化計算について説明を重ねてきました．次回は，調和振動子近似の説明からpsi4における振動数計算について説明することで計算化学について理解を深めていきたいと思います．

＞＞次の記事：「psi4における振動数計算：IRスペクトルや異性体間のエネルギー差を計算」