分子構造を何らかの形でコンピュータが扱える形へと変換することが化学情報学の第一歩です.現状では化合物の有する情報を全て取り込むことが可能な表現方法は知られていませんから,その後の分析の興味によって,化合物のどの情報を残しどの情報を捨てるかを決めた上で.変換する必要があります.
今回取り扱う「クーロン行列(Coulomb matrix)」も分子の表現方法の1つになります.特に
- 分子の立体座標
- 原子番号
の情報を基にして,分子の並進・回転操作に対して不変な変換を実現しています.
“Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning” Phys. Rev. Lett. 2012, 108, 058301.
クーロン行列とは
「ケミカルスペースプロジェクトとGDBデータベース」という記事で紹介したGB13データベースから,重原子の数が7個以下の分子に対して混成汎関数であるPBE0を用いて最適化した構造とエネルギーが含まれているのがQM7データセットです.
QM7が発表された論文の著者らは「シュレディンガー方程式から分子のエネルギーが求めるのに必要な情報は,分子内の全ての原子の種類とその座標」であるため,この情報を入力としてエネルギーを推定する機械学習モデルの構築が可能と考えました.
外部の座標軸を基にした分子のXYZ座標は分子の描画には便利な表現方法ですが,機械学習モデルにとっては好ましくない表現です.これは同じ分子を回転させたり,平行移動させてもその分子のエネルギーは変わりませんが,これら操作によって分子の3次元座標は変わってしまうためです.
クーロン行列は分子の並進・回転操作に対して不変な表現方法として,
$$ M = \left ( \begin{array}{ll} 0.5Z_i ^{2.4} & \ (i\ =\ j) \\ \frac{Z_i \times Z_j}{|\ R_i – R_j\ |} &\ (i\ \neq\ j) \ \end{array} \right . $$
で表現されます.対角要素は「原子のエネルギー」を,非対角要素は「クーロン反発」をコードしていると考えられます.
なお上記のクーロン行列の定義から,分子内の原子の順番を変えてしまうと異なる行列が得られる点に注意してください.
RDKitを用いたクーロン行列の計算
RDKitでは2020.03のアップデートからクーロン行列を計算するメソッドが追加されました.RDKitのMOLオブジェクトを渡すことで,rdkit.rdBase._vectdオブジェクトのタプルとしてクーロン行列が得られます.下記のコードではエタノールに対して計算を行い,numpy配列に変換しています.
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem
import numpy as np
print('rdkit version: ', rdBase.rdkitVersion)
# rdkit version: 2020.03.1
ethanol = Chem.AddHs(Chem.MolFromSmiles('CCO'))
AllChem.EmbedMolecule(ethanol, AllChem.ETKDG())
np.array(AllChem.CalcCoulombMat(ethanol))
array([[36.8581052 , 23.63625731, 20.55037573, 5.37460683, 5.49640183,
5.35417845, 2.73481097, 2.73767777, 2.61195049],
[23.63625731, 36.8581052 , 34.08028911, 2.83778898, 2.7347546 ,
2.83728316, 5.42533149, 5.43607405, 3.0029401 ],
[20.55037573, 34.08028911, 73.51669472, 3.3655073 , 2.42272356,
3.04345175, 3.96763228, 3.95109687, 8.08026531],
[ 5.37460683, 2.83778898, 3.3655073 , 0.5 , 0.5449894 ,
0.55454634, 0.32904401, 0.38921411, 0.46477107],
[ 5.49640183, 2.7347546 , 2.42272356, 0.5449894 , 0.5 ,
0.54292632, 0.36982712, 0.39829825, 0.29588076],
[ 5.35417845, 2.83728316, 3.04345175, 0.55454634, 0.54292632,
0.5 , 0.42263221, 0.32630447, 0.4395109 ],
[ 2.73481097, 5.42533149, 3.96763228, 0.32904401, 0.36982712,
0.42263221, 0.5 , 0.5410353 , 0.39203258],
[ 2.73767777, 5.43607405, 3.95109687, 0.38921411, 0.39829825,
0.32630447, 0.5410353 , 0.5 , 0.35615831],
[ 2.61195049, 3.0029401 , 8.08026531, 0.46477107, 0.29588076,
0.4395109 , 0.39203258, 0.35615831, 0.5 ]])
クーロン行列計算の実装
RDKitにもクーロン行列の計算が実装されていますが,ここでは理解を深めるために自分で実装してみます.
以下のコードでは
- get_dist:RDKitのコンフォマーオブジェクト中の指定した原子間の距離を求める関数
- gen_coulomb_matrix:RDKitのMOLオブジェクトを受け取り,クーロン行列をnumpy配列として返す関数
を実装しています.クーロン行列の対称性を利用することで,後者の関数の計算量を減らしています.
def get_dist(conf, atomid1, atomid2):
position1 = np.array(conf.GetAtomPosition(atomid1))
position2 = np.array(conf.GetAtomPosition(atomid2))
distance = np.sqrt(np.sum((position1 - position2) ** 2))
return distance
def gen_coulomb_matrix(mol):
conformer = mol.GetConformer(-1)
n_atoms = mol.GetNumAtoms()
arr = np.zeros((n_atoms, n_atoms))
for i in range(n_atoms):
for j in range(n_atoms):
zi = mol.GetAtomWithIdx(i).GetAtomicNum()
zj = mol.GetAtomWithIdx(j).GetAtomicNum()
if i == j:
arr[i,j] = 0.5 * zi ** 2.4
elif i > j:
distance = get_dist(conformer, i, j)
arr[i,j] = zi * zj / distance
arr[j,i] = arr[i,j]
else:
continue
return arr
gen_coulomb_matrix(ethanol)
先ほどと同じ行列が得られます.
クーロン行列を用いた分子類似性の判定
「RDKitでフィンガープリントを使った分子類似性の判定」という記事ではフィンガープリントを使って分子をベクトル化し,分子同士の類似性・距離を定量化する方法としてタニモト係数などの方法を説明しました.
それではクーロン行列で表現された分子同士の類似性はどのように表現できるでしょうか?
論文の著者らはクーロン行列の固有値を大きい順に並べたベクトルεを定義し,
$$ 距離 = \sqrt{\Sigma_l |\epsilon _l – \epsilon’ _l|^2} $$
と化合物間の距離を定義しました.この際,原子数が異なる分子を比べる際は足りない数分だけεをゼロで埋めて大きさを揃えます.
化合物空間をこのように表現することで,
- 全ての分子が固有に表現できる
- 対称な原子の寄与が等しくなる(降順に並べるので)
- 原子の順番並べ替えに不変になる
という特徴が得られます.
分子間距離の実装
それでは前述の定義に従ってクーロンマトリクスから距離を求めてみましょう.線形代数関係の操作はnumpy.linalgに実装されています.
下のコードでは
- get_eigenvalues_from_matrix:クーロン行列の固有値を並べたベクトルを生成
- get_distance_mols_with_coulomb_matrix:2つのRDKitのMOLオブジェクトの距離をクーロン行列を基に算出
という関数を定義しています.その際前者ではベクトル長を与えることで,ゼロで埋める操作を行います.
最後に定義した関数を使って,論文にあるような「エタノールとピロール」と「ピロールとチオフェン」の距離を求めてみます.
def get_eigenvalues_from_matrix(mat, dim):
eigenvalues = np.sort(np.linalg.eigvals(mat))[::-1]
if dim > len(mat):
expanded_vec = np.zeros(dim)
expanded_vec[:len(mat)] = eigenvalues
else:
expanded_vec = eigenvalues
return expanded_vec
def get_distance_mols_with_coulomb_matrix(mol1, mol2):
max_n_atoms = max(mol1.GetNumAtoms(), mol2.GetNumAtoms())
mat1 = gen_coulomb_matrix(mol1)
mat2 = gen_coulomb_matrix(mol2)
eig1 = get_eigenvalues_from_matrix(mat1, dim=max_n_atoms)
eig2 = get_eigenvalues_from_matrix(mat2, dim=max_n_atoms)
distance = np.sqrt(np.sum((eig1 - eig2) ** 2))
return distance
pyrrole = Chem.AddHs(Chem.MolFromSmiles('N1cccc1'))
thiophene = Chem.AddHs(Chem.MolFromSmiles('S1cccc1'))
AllChem.EmbedMolecule(pyrrole, AllChem.ETKDG())
AllChem.EmbedMolecule(thiophene, AllChem.ETKDG())
print(get_distance_mols_with_coulomb_matrix(ethanol, pyrrole))
# 30.814354770041238
print(get_distance_mols_with_coulomb_matrix(pyrrole, thiophene))
# 286.6475905491756
論文ではそれぞれの距離は30.7と306.9ですが,DFTで最適化した立体構造を使っていますのでこの程度のズレは許容でしょう.
QM7データセット中のケミカルスペースをクーロンマトリクスで可視化
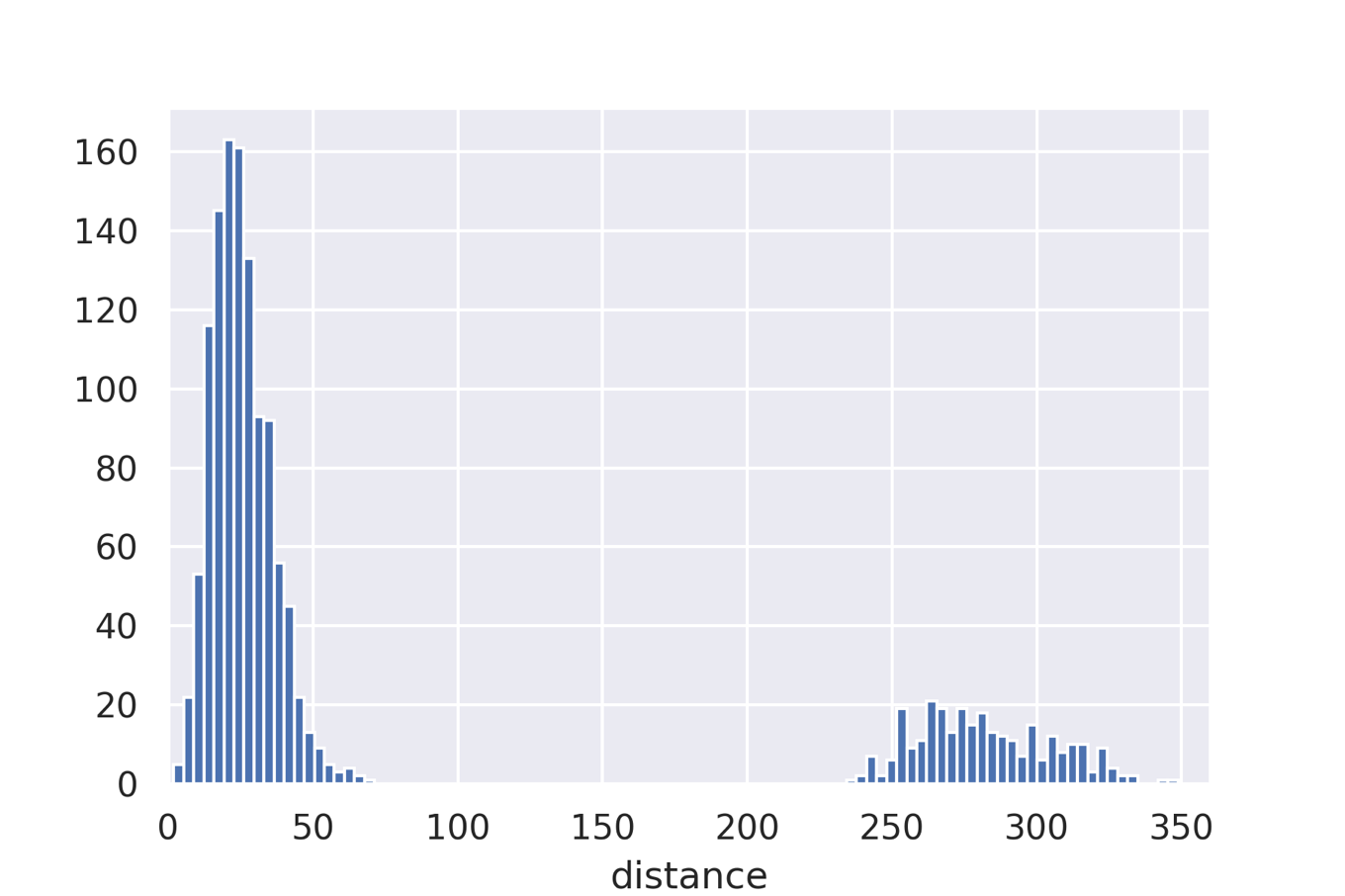
続いて「QM9は量子化学計算に基づいた機械学習用の大規模データセット」という記事で紹介したQM7データセットを使い,全分子の距離を求め論文の図1に記載されているようなヒストグラムを作成してみましょう.なお今回はQC Archiveにホストされているデータを用いています.
座標データは「molecules」とうフォルダにXYZ形式で分子毎に分かれたファイルになっています.RDKitではXYZ形式をそのまま読み込んでMOLオブジェクトとすることはできませんので,Open Babelを用いてmol形式へと変換した上で処理を行います.
下記コードでは
- XYZファイルのリストを取得
- XYZ形式をmol形式に変換してRDKitのMOLオブジェクトに変換
- 先ほど作成した関数を使って距離行列を取得
- 距離行列は対称行列なので,上三角部分を取り出し,非ゼロの部分のみを集計して可視化
という手順で処理をしています.
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import os
import pybel
## 1. XYZファイルのリストを取得
cwd = os.getcwd()
folder = os.path.join(cwd, 'molecules')
files = os.listdir(folder)
## 2. XYZをmol形式に変換し,RDKitのMOLオブジェクトに変換
mols = []
for file in files:
pybel_mol = [x for x in pybel.readfile('xyz', os.path.join(folder, file))]
rdkit_mol = Chem.MolFromMolBlock(pybel_mol[0].write('mol'), removeHs=False)
mols.append(rdkit_mol)
## 3. 距離行列を計算
distant_mat = np.zeros((len(mols), len(mols)))
for i, mol1 in enumerate(mols):
for j, mol2 in enumerate(mols):
if i >= j:
distant_mat[i,j] = get_distance_mols_with_coulomb_matrix(mol1, mol2)
distant_mat[j,i] = distant_mat[i,j]
## 4. 上三角成分を取りだし可視化
upper = np.triu(distant_mat)
upper_values = upper[np.nonzero(upper)].flatten()
plt.hist(upper_values, bins=100)
plt.xlabel('distance')
plt.xlim(0,360)
論文通り,30前後をピークとした部分と280前後をピークとする部分からなる分布が得られています.
ランダム化クーロン行列
numpy.argsort(ndarray)
前述のようにクーロン行列は分子内の原子の順番を変える操作によって表記が変わってしまいますので,このままでは機械学習モデルの入力としてはやや不適切です.
QM7bデータセットを発表した論文中で,著者らはこの問題に対する対策として「ランダム化クーロン行列」を報告しています.
“Machine learning of molecular electronic properties in chemical compound space” New J. Phys. 2013, 15, 095003.
ランダム化クーロン行列では単純に全ての原子の順番をランダムにするのではなく,以下の方法に従って原子の順番を入れ替えます.
- 対象とするクーロン行列の各行について2次のノルムを取る
- 平均0,分散1の標準正規分布からクーロン行列の行数分だけサンプルを取得する
- 1で得たノルムを並べたベクトルに2で得たノイズベクトルを足し,降順に並べる
- 降順に整列した3のベクトルを与えるインデックスの順番に,もとのクーロン行列の順番を並べ替える
この作業を実装したものが下のコードになります.
なおRDKitのCalcCoulombMatrixのドキュメントには複数のランダム化クーロン行列を計算すると記載がありますが,現在の実装で得られるのは通常のクーロン行列のようです.
def gen_randomized_coulomb_matrix(matrix):
dim = len(matrix)
norm = np.linalg.norm(matrix, axis=1)
eps = np.random.randn(dim)
argsort = np.argsort(norm + eps)[::-1]
return matrix[argsort][:,argsort]
それではランダム化クーロン行列で並べ替えられた原子の順番の意味を見てみましょう.サンプルとしてトリフルオロ酢酸を使ってみます.
cf3 = Chem.MolFromSmiles('FC(F)(F)C(=O)O')
cf3 = Chem.AddHs(cf3)
AllChem.EmbedMolecule(cf3, AllChem.ETKDGv3())
print(Chem.MolToXYZBlock(cf3))
各原子の番号は以下のようになります.
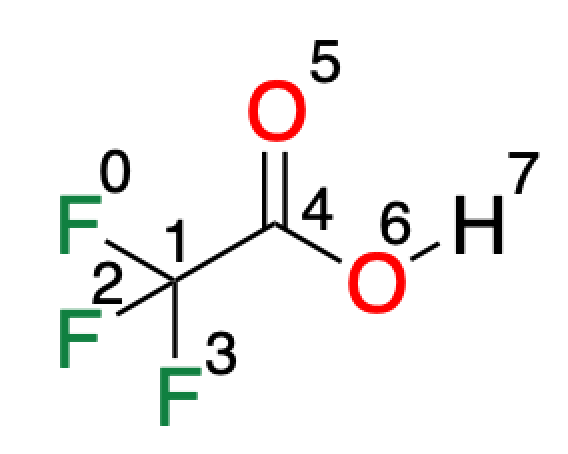
8 F -1.862577 0.741082 0.066203 C -0.906970 -0.229637 0.089326 F -0.970805 -0.988304 1.266901 F -1.038421 -1.077407 -1.017389 C 0.422649 0.410812 0.082517 O 0.479398 1.660903 0.058371 O 1.601289 -0.291838 0.101267 H 2.275438 -0.225610 -0.647196
mat_cf3 = coulomb_matrix(cf3) print(mat_cf3)
クーロン行列は以下のようになりました.
[[97.53309975 39.63719848 35.42658225 35.65720106 23.38648228 28.61521425 19.9183092 2.08870123] [39.63719848 36.8581052 38.50927649 38.56344315 24.39287334 20.47263766 19.13068059 1.8368131 ] [35.42658225 38.50927649 97.53309975 35.41717176 23.45167162 22.13349794 24.75493838 2.3407392 ] [35.65720106 38.56344315 35.41717176 97.53309975 22.90251923 21.74901541 24.22090596 2.61510138] [23.38648228 24.39287334 23.45167162 22.90251923 36.8581052 38.35055838 34.97727325 2.87007732] [28.61521425 20.47263766 22.13349794 21.74901541 38.35055838 73.51669472 28.41310326 2.9644856 ] [19.9183092 19.13068059 24.75493838 24.22090596 34.97727325 28.41310326 73.51669472 7.92483514] [ 2.08870123 1.8368131 2.3407392 2.61510138 2.87007732 2.9644856 7.92483514 0.5 ]]
print(gen_randomized_coulomb_matrix(mat_cf3))
ランダム化クーロン行列は次のようになります.
[[97.53309975 35.42658225 35.65720106 28.61521425 19.9183092 39.63719848 23.38648228 2.08870123] [35.42658225 97.53309975 35.41717176 22.13349794 24.75493838 38.50927649 23.45167162 2.3407392 ] [35.65720106 35.41717176 97.53309975 21.74901541 24.22090596 38.56344315 22.90251923 2.61510138] [28.61521425 22.13349794 21.74901541 73.51669472 28.41310326 20.47263766 38.35055838 2.9644856 ] [19.9183092 24.75493838 24.22090596 28.41310326 73.51669472 19.13068059 34.97727325 7.92483514] [39.63719848 38.50927649 38.56344315 20.47263766 19.13068059 36.8581052 24.39287334 1.8368131 ] [23.38648228 23.45167162 22.90251923 38.35055838 34.97727325 24.39287334 36.8581052 2.87007732] [ 2.08870123 2.3407392 2.61510138 2.9644856 7.92483514 1.8368131 2.87007732 0.5 ]]
ランダムに入れ替えられた原子を詳しく調べるために,以下のコードでは原子の順番だけに着目してランダム化クーロン行列を5回生成します.
def return_sorted_index(matrix):
dim = len(matrix)
norm = np.linalg.norm(matrix, axis=-1)
eps = np.random.randn(dim)
argsort = np.argsort(norm + eps)[::-1]
return argsort
atom_list = [atom.GetSymbol() for atom in cf3.GetAtoms()]
for _ in range(5):
atoms = return_sorted_index(mat_cf3)
print(pd.Series(atom_list)[atoms])
2 F 0 F 3 F 5 O 6 O 1 C 4 C 7 H dtype: object 3 F 0 F 2 F 6 O 5 O 1 C 4 C 7 H dtype: object 2 F 3 F 0 F 5 O 6 O 1 C 4 C 7 H dtype: object 0 F 2 F 3 F 5 O 6 O 1 C 4 C 7 H dtype: object 3 F 0 F 2 F 6 O 5 O 1 C 4 C 7 H dtype: object
ランダム化クーロン行列の作成によって並び替えられた原子いずれも「フッ素,酸素,炭素,水素」の順番になっています.3つのフッ素の中での順番を見てみると,3つのフッ素が等価に扱われランダムに並んでいることがわかります.酸素についても同様です.一方で炭素の並びは毎回同一です.
このように,ランダム化クーロン行列では対称性のある化学的に等価な原子内でのみ順番を入れ替えます.論文の著者らの検討では,このようにランダム化したクーロン行列を入力として用いた方が単に原子番号順に並べ替えたクーロン行列よりも機械学習モデルの精度が高かったと報告されています.
終わりに
今回は「クーロン行列は分子の回転・並進操作に不変な化合物の表現法」という話題について,
- クーロン行列とは何か
- RDKitを用いたクーロン行列の計算方法
- numpyを用いたクーロン行列計算の実装
- クーロン行列を用いた分子間の距離の定義と実装
- ランダム化クーロンマトリクスの説明と実装
などについて触れてきました.特に分子をベクトル化する際に,並進・回転操作に対する不変性を考えることはクーロン行列に限らず大切な概念です.
クーロン行列と自然言語処理のアイデアから派生した分子のベクトル化法として,分子内の結合の集合を考える「Bag of Bonds (BoB)」というものがあります.次回はこちらを見ていきたいと思います.なおRDKitには現状ではBoBを求める関数は実装されていませんが,GitHubのPRによると近々実装されそうです.
“Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space” J. Phys. Chem. Lett. 2015, 6, 2326-2331.
コメント