「MOLファイル・SDFとはどんな化学情報ファイルなのか?」という記事では,原子をノード,結合をエッジと見なすことで分子はグラフと考えられることに触れました.またどの原子とどの原子の間に結合が存在するかをリストとして管理する「結合リスト」について説明しました.
グラフ構造は分子に限らず現実世界に数多く見られ,その特性や探索方法が活発に研究されています.例えばpythonではscipy.sparse.csgraphやNetworkXに様々なグラフ関連アルゴリズムが実装されています.
この記事ではRDKitにおける化合物のグラフ構造の取り扱いについて,特にChem.rdmolopsモジュールに実装されているメソッドを中心に説明していきます.
化合物のグラフ表現
グラフではある原子が他の原子とどのように繋がっているかを表現することができます.原子同士のつながり方,トポロジーだけが重要であり結合距離などは考慮しません.
まずはイソペンタンを例にして考えてみます.
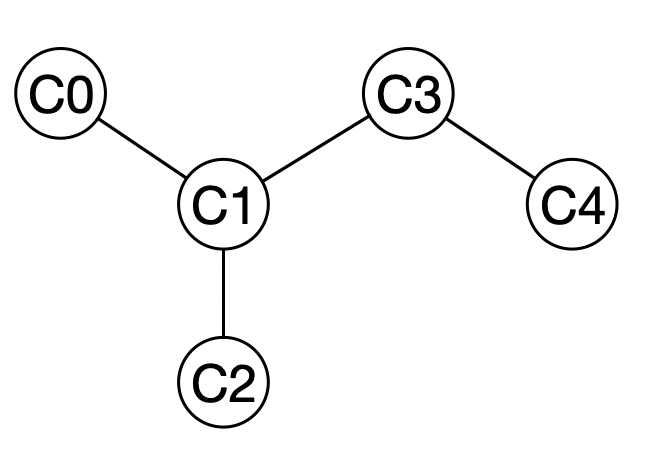
隣接行列
二つの原子の間に
- 結合がある場合を1
- 結合がない場合を0
とすると,全ての原子間の結合は以下のような行列で表現できます.このような表現をグラフの「隣接行列」(adjacency matrix)といいます.結合が2つある場合には2を用いることもあります.
また各原子に接続している結合の数をその原子の「次数」(degree)といいます.隣接行列はその定義から対称行列になります.
$$ \left(
\begin{array}{ccccc}
0&1&0&0&0 \\
1&0&1&1&0 \\
0&1&0&0&0 \\
0&1&0&0&1 \\
0&0&0&1&0 \\
\end{array}
\right) $$
距離行列
二つの原子の間の最短距離を記した行列を「距離行列」(distance matrix)といいます.この場合の距離とはいくつの辺を介して繋がっているかを示すトポロジカル距離になります.
先ほどのイソペンタンの場合ですと以下のように表現できます.距離行列も対称行列です.
$$ \left(
\begin{array}{ccccc}
0&1&2&2&3 \\
1&0&1&1&2 \\
2&1&0&2&3 \\
2&1&2&0&1 \\
3&2&3&1&0 \\
\end{array}
\right) $$
RDKitを用いた隣接行列と距離行列
Chem.rdmolops.GetDistanceMatrix(mol)
RDKitでは分子をグラフとして扱う操作が多数実装されています.これらのメソッドはChem.rdmolopsモジュールに実装されています.
本モジュール中のメソッドはChemモジュール中でimportされていることから,Chemモジュールからダイレクトに使うことができます.以下の例ではイソペンタンの隣接行列と距離行列を取得しています.
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw
from rdkit.Chem.Draw import IPythonConsole, rdMolDraw2D
from IPython.display import SVG
from matplotlib.colors import ColorConverter
import numpy as np
print('rdkit: ', rdBase.rdkitVersion)
print('numpy: ', np.__version__)
# rdkit: 2020.03.1
# numpy: 1.17.4
mol = Chem.MolFromSmiles('CC(C)CC')
print(Chem.GetAdjacencyMatrix(mol))
print(Chem.GetDistanceMatrix(mol))
どちらのメソッドでもnumpy配列として得られます.
[[0 1 0 0 0] [1 0 1 1 0] [0 1 0 0 0] [0 1 0 0 1] [0 0 0 1 0]] [[0. 1. 2. 2. 3.] [1. 0. 1. 1. 2.] [2. 1. 0. 2. 3.] [2. 1. 2. 0. 1.] [3. 2. 3. 1. 0.]]
グラフにおけるパス
グラフ上のある点からある点へ至るルートのうち,同じ点を通過しないルートを「パス」といいます.距離行列中の値は,必然的にいくつかのパスのうち最短のものが記載されていることになります.
ここではファビピラビルを例としていくつか例をみていきます.
m = Chem.MolFromSmiles('C1=C(N=C(C(=O)N1)C(=O)N)F')
view = rdMolDraw2D.MolDraw2DSVG(300, 300)
option = view.drawOptions()
option.addAtomIndices=True
view.DrawMolecule(m)
view.FinishDrawing()
svg = view.GetDrawingText()
SVG(svg)
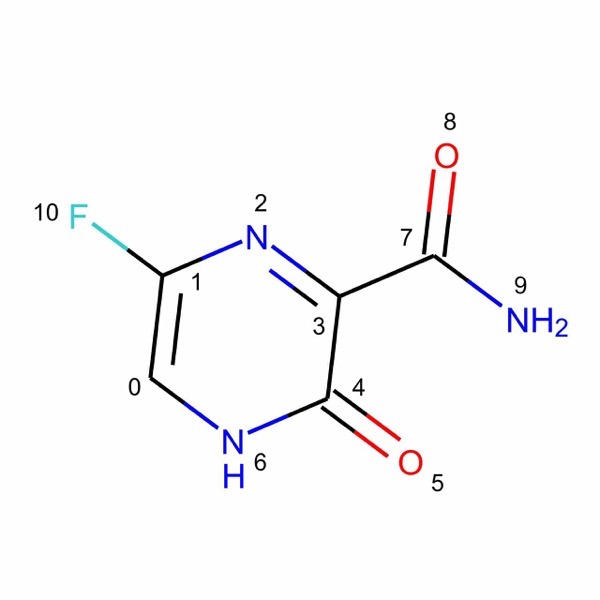
以下のコードではRDKitの新しい構造描画モジュールrdMolDraw2Dを多用しています.「RDKitでの構造式描画を詳しく解説」という記事で使い方を説明していますので,適宜参照してみてください.
RDKitを用いた最短経路パスの取得
GetShortestPathメソッドではその名の通り,ある原子からある原子へと至る最短経路パスが経由する原子のタプルとして得られます.
以下のコードでは
- 原子0から原子7
- 原子6から原子10
の二つを例に実際に構造式上で確認してみます.
p1 = Chem.GetShortestPath(m, 0, 7) # (0, 1, 2, 3, 7)
p2 = Chem.GetShortestPath(m, 6, 10) # (6, 0, 1, 10)
m.GetAtomWithIdx(0).SetProp('atomNote', '0')
m.GetAtomWithIdx(7).SetProp('atomNote', '7')
m.GetAtomWithIdx(6).SetProp('atomNote', '6')
m.GetAtomWithIdx(10).SetProp('atomNote', '10')
v = rdMolDraw2D.MolDraw2DSVG(600, 300, 300, 300)
v.DrawMolecules([m, m], highlightAtoms=[p1, p2])
v.FinishDrawing()
svg = v.GetDrawingText()
SVG(svg)
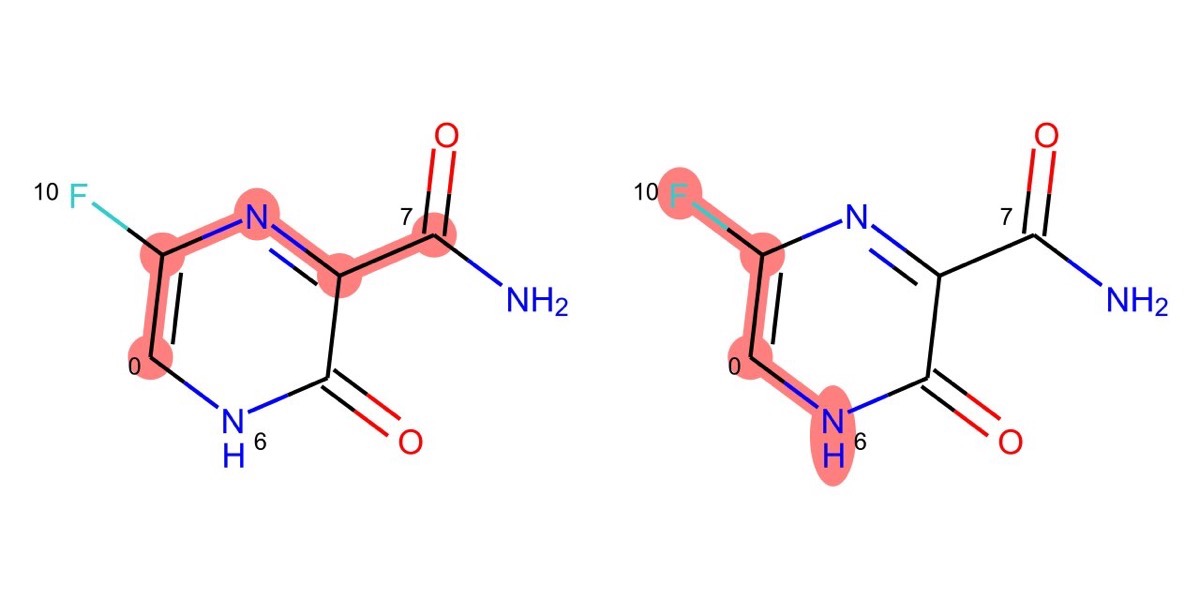
雰囲気がつかめたでしょうか?
RDKitを用いた一定長のパスの探索
FindAllPathsOfLengthNメソッドでは,分子中の指定した長さのパスを全て探索します.戻り値は経由する結合のタプルになります.原子ではない点に注意してください.
このメソッドはrootedAtAtomオプションを設定することで,どの原子からのパスを探索するかを指定できます.
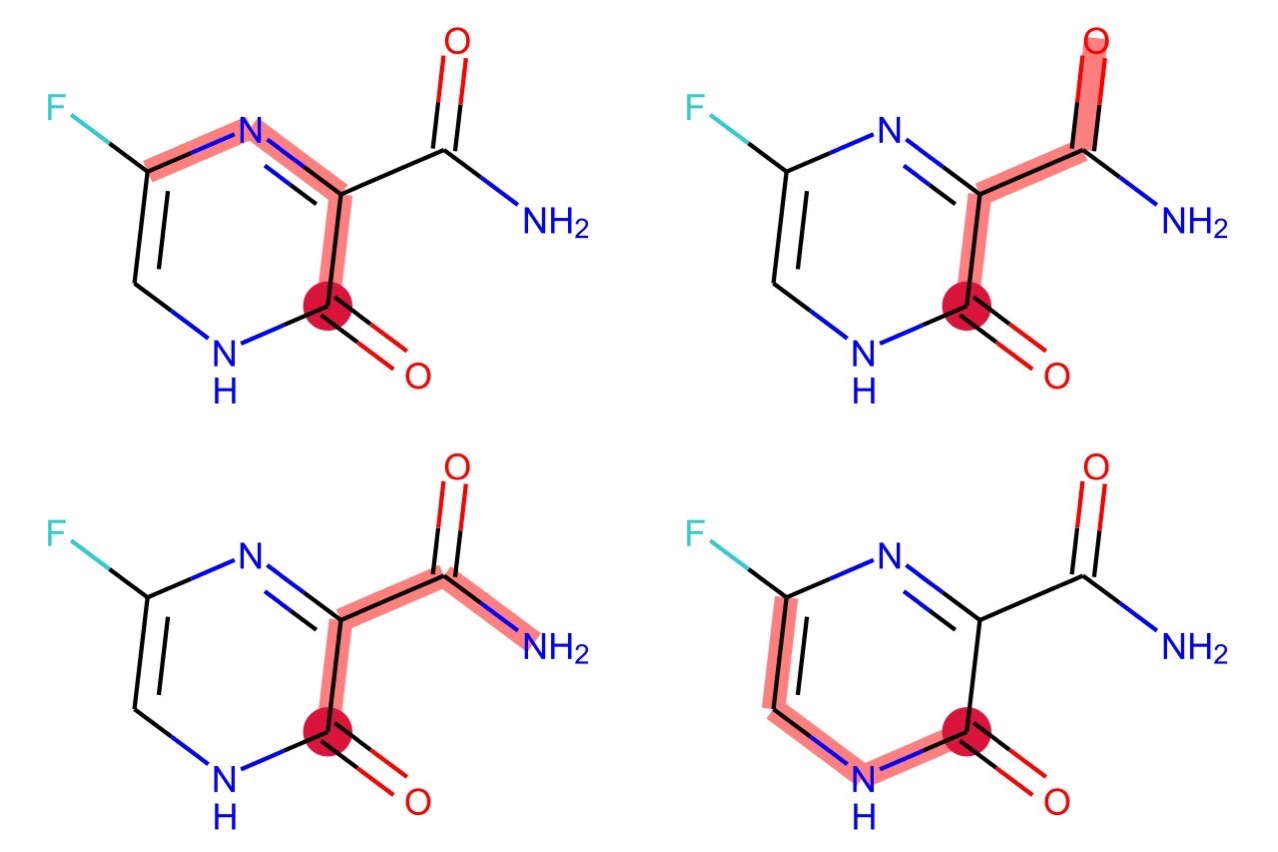
下のコードでは原子4を始点として長さ3のパスを全て探索しています(4つあります).それぞれをhighlightBondsに設定することで描画しています.見やすいように始点も別にハイライトしてあります.
for atom in m.GetAtoms():
atom.ClearProp('atomNote')
crimson = ColorConverter.to_rgb('crimson')
paths = [tuple(i) for i in Chem.FindAllPathsOfLengthN(m, length=3, rootedAtAtom=4)]
v = rdMolDraw2D.MolDraw2DSVG(600, 400, 300, 200)
v.DrawMolecules([m] * len(paths), highlightBonds=paths,
highlightAtoms=[[4]] * len(paths),
highlightAtomColors=[{4: crimson}] * len(paths))
v.FinishDrawing()
svg = v.GetDrawingText()
SVG(svg)
部分グラフ
あるグラフに対して,頂点と辺の部分集合がグラフを形成するとき,それを「部分グラフ」(subgraph)と呼びます.
分子構造の場合は,分子内の部分構造が部分グラフになります.
RDKitを用いた部分グラフの扱い方
Chem.rdmolops.FindUniqueSubgraphsOfLengthN(mol, length)
Chem.rdmolops.FindAllSubgraphsOfLengthMToN(mol, min, max)
何れのメソッドもrootedAtAtomオプションが設定可能です.部分グラフの場合は始点というよりも,グラフ内に含有される程度の意味あいになります.
v = rdMolDraw2D.MolDraw2DSVG(680, 600, 170, 200)
subgraphs = [tuple(i) for i in Chem.FindUniqueSubgraphsOfLengthN(m, length=3, rootedAtAtom=4)]
v.DrawMolecules([m] * len(subgraphs), highlightBonds=subgraphs,
highlightAtoms=[[4]] * len(subgraphs),
highlightAtomColors=[{4: crimson}] * len(subgraphs))
v.FinishDrawing()
svg = v.GetDrawingText()
SVG(svg)
パスと異なり部分グラフは分岐を含むことが見てとれます.そのため,部分グラフにおけるlengthは部分構造に含まれる結合数に一致します.
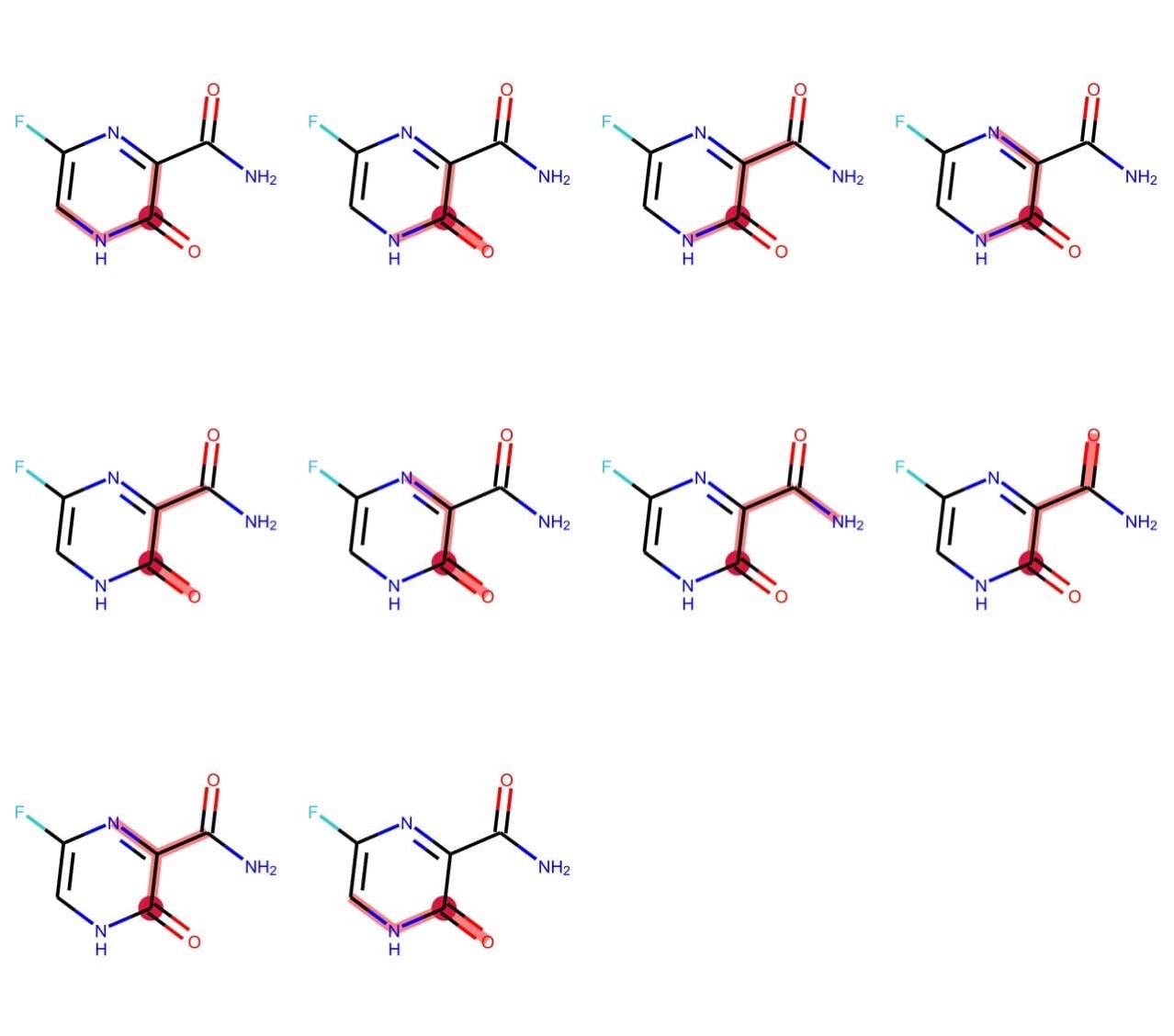
もう一つ例として,原子0を始点とする距離0から2までの部分グラフを全て求めてみましょう.
for i, j in enumerate(Chem.FindAllSubgraphsOfLengthMToN(m, min=0, max=2, rootedAtAtom=0)):
print('length {}: {}'.format(i, j))
length 0: [] length 1: [(0,), (10,)] length 2: [(0, 9), (0, 1), (0, 10), (10, 5)]
こちらも描画してみると以下のようになります.
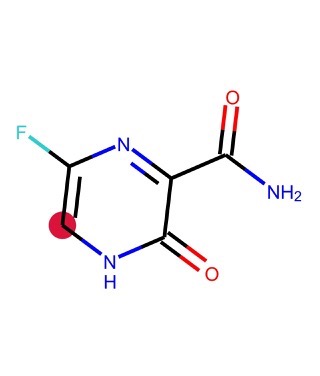
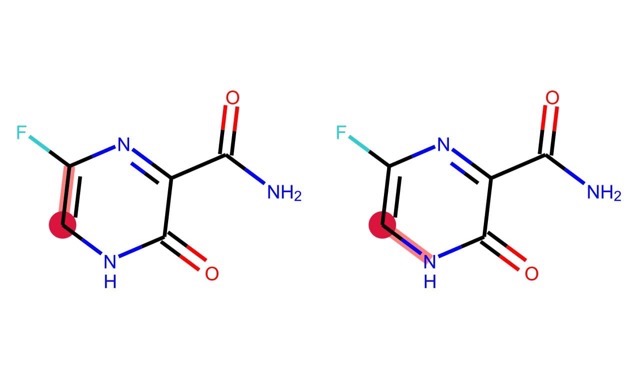
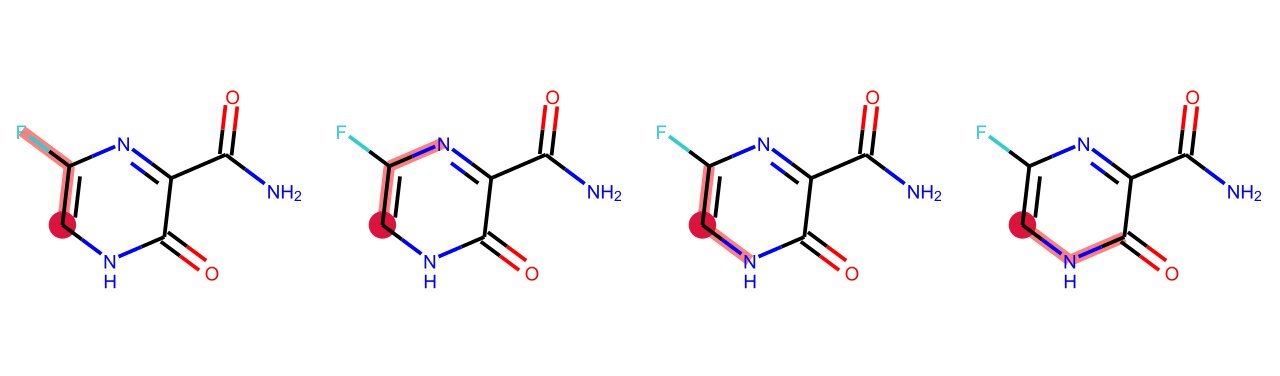
分子の表現方法と次元
分子の特性を表現する方法として分子記述子があります.また化合物のどのような情報を表すかによって,分子記述子の次元を考えることがあります.
例えば
- 「分子量」は0Dの記述子
- 「分子内のアミド結合の数」は1Dの記述子
です.化合物のグラフ構造から得られる表現は2Dの記述子といえます.
分子のトポロジーを1つの数字とした表現法
化合物をグラフとして扱うことで,分子のトポロジーを取り入れた表現が可能になると期待できます.情報を1つの値として代表する記述子としては以下のようなものが挙げられます.
Wiener指数
Wiener指数(W)は非環状炭化水素のグラフGについて,「あらゆる2つの炭素間の距離の和」として提唱されました.
$$ W(G) = \displaystyle \sum_{i=1}^N \displaystyle \sum_{j > i}^N d_{i,j} $$

イソペンタンの場合,
C0について
$$ 1 + 2 + 2 + 3 = 8 $$
C1について
$$ 1 + 1 + 2 = 4 $$
C2について
$$ 2 + 3 = 5 $$
C3について
$$ 1 $$
となることからWiener指数は18と求まります.
お気づきの方もいらっしゃるでしょうが,Wiener指数は距離行列の上三角成分の和に等しいため,以下のように求めることが可能です.
d = Chem.GetDistanceMatrix(mol) print(np.triu(d).sum()) # 18.0
logP
logP自体は実験によって求められる値ですが,「ケモインフォマティクスとLogP計算:CLogPのCは”calculated”ではありません」という記事でも紹介したように様々な手法によって推定する方法が開発されています.
CLogPは分子のフラグメント(部分構造)毎にlogPへの寄与を求め,その総和によってlogPを推定する方法です.2D(トポロジカル)記述子の代表例と言えます.
TPSA
極性表面積(PSA)自体は分子の立体構造が必要な3D記述子です.しかし「トポロジカル極性表面積は計算コストの低い推定PSA」という記事で紹介したように,分子の部分構造に着目して精度よくPSAを推定する,トポロジカルPSA(TPSA)という方法が広く使われています.TPSAは2D記述子です.

トポロジーをベクトルとした分子の表現方法
前項で示したように分子全体の特性を1つの数字として表してしまうと,多くの情報が失われてしまいます.そのため多次元ベクトルを用いることで,より多くの情報を取り込もうとするのが自然な方針でしょう.
フィンガープリント
「RDKitでフィンガープリントを使った分子類似性の判定」という記事で説明したように,MACCS KeyやDaylightなどのフィンガープリントは歴史的には化合物データベース開発の流れで発展してきました.
フィンガープリントが徐々にQSARにおける特徴量ベクトルとしても使われるようになるにつれ,より多くの情報を取り込んだフィンガープリントが開発されるようになりました.
「アトムペアやドナーアクセプターペアフィンガープリントは分子の形状を捉えた化学表現」で解説した全ての原子間のトポロジカル距離を取り込むアトムペアフィンガープリントや,中心原子から一定のトポロジカル距離にある原子を考慮するMorganフィンガープリント(ECFP)が2D記述子の代表例と言えます.

終わりに
今回は「化合物の隣接行列,距離行列,Wiener指数:RDKitを用いたグラフの扱い方」という話題について,
- 化合物のグラフ表現として隣接行列と距離行列
- グラフのパスや部分グラフ
- RDKitを用いた分子のグラフ表現の扱い方
- トポロジカル情報を組み入れた記述子
などについて概説しました.今回の内容は業務にすぐに役立つ内容ではないかもしれません.こういった内容をしっかりと押さえることが盤石な基礎を築き,最先端の内容を理解する近道になると思います.
コメント