多数の化合物から構造的に多様なライブラリーを構築するためには,
- クラスタリング法
- 距離ベースの方法
- 区分けをベースとした方法
- 最適化手法を用いる方法
といった4つの手法が代表的です.
クラスタリング法の中でも,「RDKitとk平均法による化合物の非階層型クラスタリング」という記事では非階層型クラスタリング法であるk平均法を使って化合物のクラスタリングを行いました.
今回は階層型クラスタリング手法の1つであるウォード法による凝集型クラスタリングを行い,化合物ライブラリーから「多様な」化合物を選択していきたいと思います.
ウォード法はRDKitにも実装されていますが,今回はpythonの機械学習用ライブラリの定番であるscikit-learnを用いていきたいと思います.

クラスタリングに用いる分子の準備
今回もナミキ商事の運営するChemCupidからダウンロードした,カタログの新規追加分の分子を収めたSDFを使いたいと思います.
塩の化合物は扱いにくいので,NScodeが0000で終わるもの(フリー体)のみを読み込んでいます.全部で66005個の分子になりました.
最後に分子の順番をランダムにシャッフルします.クラスタリングには最初の5000個を用いることにします.
### ライブラリのインポート
from rdkit import rdBase, Chem, DataStructs
from rdkit.Chem import AllChem
from rdkit.Chem.Draw import rdMolDraw2D, IPythonConsole
import numpy as np
%matplotlib inline
print(rdBase.rdkitVersion) ### 2017.03.3
### 分子の読み込み
suppl = Chem.SDMolSupplier('./Namiki_NEW_201807_0001.sdf')
mols_free = [x for x in suppl if x is not None if x.GetProp('NScode').endswith('0000')]
len(mols_free) ### 66005
### シャッフル
np.random.seed(1234)
np.random.shuffle(mols_free)
凝集型クラスタリングの種類
今回扱うウォード法という手法は凝集型クラスタリングと呼ばれるものです.この方法では最初はすべてのデータを別個のグループとして扱います.その後に最も「類似」した2つのデータを1つにまとめて扱い,また次の「類似」したデータを...というように徐々にデータの集団を形成していきます.そのため凝集型クラスタリングという名前がついています.
「最も類似した」クラスタを決定するための基準を連結法(linkage)と呼び,いくつかの方法がよく使われています.scikit-learnには以下の3つの方法が実装されています.
- ウォード法
- 平均連結法
- 完全連結法
ウォード法
クラスタ内の分散の増加が最小となるように2つのクラスタを選択します.scikit-learnのデフォルト設定で,クラスタサイズが均一に近くなる傾向があります.多くの場合はこれでうまくいきます.
平均連結法
クラスタ間のすべての点間の距離の平均が最小となるように2つのクラスタを選択します.
完全連結法
クラスタ間の点間の距離の最大値が最小となるように2つのクラスタを選択します.
scikit-learnを用いたウォード法によるクラスタリング
pythonの機械学習用ライブラリであるscikit-learnには凝集型クラスタリングが実装されていますので,まずはそちらを使ってみましょう.デフォルトではウォード法が連結法として選択されています.
Morganフィンガープリントの生成と距離行列の計算
DataStructs.BulkTanimotoSimilarity(refFP, FP_list, returnDistance=True)
まずはクラスタリングを行うための入力データとしてフィンガープリントを作成し,それをもちいて距離行列を作成します.returnDistance=Trueオプションを設定することでBulkTanimotoSimilarityの出力が「1 – タニモト係数」によって計算した距離に変わりますので,それを利用して距離行列を作成しています.
なおscikit-learnのインプットはnumpy配列である必要がありますので,最後に変換を施しています.
morgan_fp = [AllChem.GetMorganFingerprintAsBitVect(x,2,2048) for x in mols_free] dis_matrix = [DataStructs.BulkTanimotoSimilarity(morgan_fp[i], morgan_fp[:5000],returnDistance=True) for i in range(5000)] dis_array = np.array(dis_matrix)
ウォード法によるクラスタリングの実行
sci-kit learnでは,凝集型クラスタリングはcluster.AgglomerativeClusteringに実装されています.先ほど述べたようにデフォルトの連結法はウォード法ですが,linkageオプションで変更可能です.
| linkage | 説明 |
|---|---|
| “ward” | ウォード法 |
| “average” | 平均連結法 |
| “complete” | 完全連結法 |
今回はウォード法を用いて6個のクラスタに分割することにします.なおscikit-learnでは指定したクラスター数に達した時点でモデル構築は終了します.
import pandas as pd from sklearn.cluster import AgglomerativeClustering ward = AgglomerativeClustering(n_clusters=6) ward.fit(dis_array) pd.value_counts(ward.labels_)
k平均法と比べるとクラスタのサイズに偏りがあることが見てとれます.
| クラス | 個数 |
|---|---|
| 1 | 1407 |
| 2 | 1136 |
| 0 | 1132 |
| 4 | 605 |
| 3 | 532 |
| 5 | 188 |
ウォード法で分類した各クラスターから分子の抽出
続いて実際に各クラスターからランダムに分子を抽出して,構造を見比べてみましょう.下のコードでは辞書型にクラスタ名と分子を対応させた後に,ランダムに1つの分子を選択しています.
ward_library = {i: [] for i in range(6)}
for n,j in enumerate(ward.labels_):
ward_library[j].append(mols_free[n])
selected_compounds = [np.random.choice(ward_library[i]) for i in range(6)]
選択された分子の構造は以下のとおりでした.
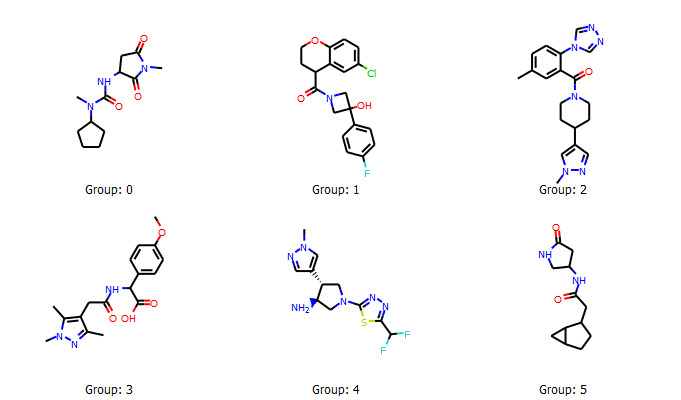
クラスタリング結果のデンドログラムによる可視化
scipy.cluster.hierarchy.dendrogram(linked_array)
ウォード法などの凝集型クラスタリングが階層型とよばれる理由は,1つ1つのデータが集まって集団を形成していく過程を図にすると樹形図のようなグラフが描けるためです.このようなグラフを「デンドログラム」と呼びます.
2018年9月現在,scikit-learnではデンドログラムの作図はサポートされていませんが,scipy.clusterモジュールにward法とデンドログラムの作図が実装されていますので,そちらを使ってみます.
scipyでのward法はscikit-learnとは異なり,リンク配列を作成します.この配列を使うとデンドログラムを用いた可視化が可能になります.
from scipy.cluster import hierarchy
linked_array = hierarchy.ward(dis_array)
hierarchy.dendrogram(linked_array)
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [34.5,34.5], '--', c='gray')
ax.plot(bounds, [55,55], '--', c='gray')
ax.text(bounds[1], 55, ' 3 clusters', va='center')
ax.text(bounds[1], 34.5, ' 6 clusters')
plt.xlabel('Compounds', fontsize=12)
plt.xticks([])
plt.ylabel('Cluster distance', fontsize=12)
plt.title('Dendrogram for Ward method', fontsize=14)
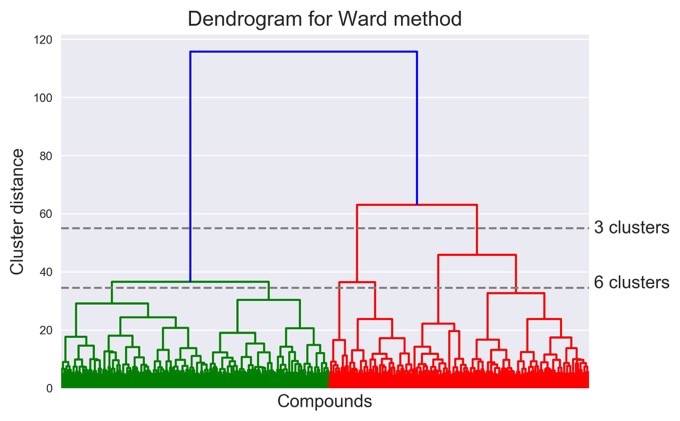
デンドログラムではx軸が各データを表します.凝集型クラスタリングではデンドログラムの下から上へと眺めていきます.
今回は5000個ものデータがありますので,潰れてしまっていますが,個々のデータが徐々に集団を形成していっているのがおわかり頂けると思います.y軸はクラスタ間の距離を表します.
またx軸に水平な線と交わった本数がクラスタの数になります.今回は2つの線を入れています.上側の線は3つ(青1,赤2)と交わっていているため,この段階が3つのクラスターに分かれている状態になります.同様に下側の線は6つ(緑2,赤4)と交わっているので,6つのクラスターにわかれている状態です.すなわち,先ほどのscikit-learnのモデルではこの辺りの段階のモデルになります.
各クラスター内の分子数を数えた際に,1000を超える大きなクラスタが3つ存在していましたが,それらはおそらく左側の緑のクラスタ2つと,赤の1番右側のクラスタであると考えられます.また最も小さいクラスターは188個の分子を含むだけでしたが,そのクラスターは赤の1番左側のクラスターに相当すると考えられます.
このようにデンドログラムを用いることで,各データがどのようにクラスタリングされていくかを可視化することが可能になります.
クラスタリングのような教師なし学習では,いくつのクラスタに分けるのが適切かを事前に知ることは困難です.デンドログラムを眺めながら探索的にクラスタ数を変えていくことで,集団全体の特徴をうまく代表するようなクラスタに分けることができるかもしれません.例えば今回であれば,左の緑の部分はいずれも類似していると考えられるので,3または4つ程度のクラスターに分けてもよかったかもしれません.
主成分分析による次元削減
クラスタリングの結果を可視化する別の方法が次元削減を用いた方法です.今回のデータは1つの化合物が5000個の特徴量で表された5000次元のデータになっていますので,このまま可視化することはできません.そこで,データセットの特徴を残しながら我々が理解できる形(2,3次元)へと次元削減を行う必要があります.このような目的に最もよく使われるのが「主成分分析(PCA; Principle Component Analysis)」という手法です.
主成分分析はscikit-learnではsklearn.decompositionに実装されています.ここでは2次元データへと変換することとし,散布図上でのマーカーの色にクラスター番号を用いることで化合物空間内での分類具合を可視化してみます.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
### モデル構築・データ変換
pca.fit(dis_array)
dis_pca = pca.transform(dis_array)
### 可視化
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
ax.scatter(dis_pca[:,0], dis_pca[:,1], s=50, c=ward.labels_[:5000], cmap='Paired', alpha=0.5)
ax.set_xlabel('PCA 1', fontsize=20)
ax.set_xticklabels([])
ax.set_ylabel('PCA 2', fontsize=20)
ax.set_yticklabels([])
ax.set_title('6-Clusters by sklearn ward', fontsize=28)
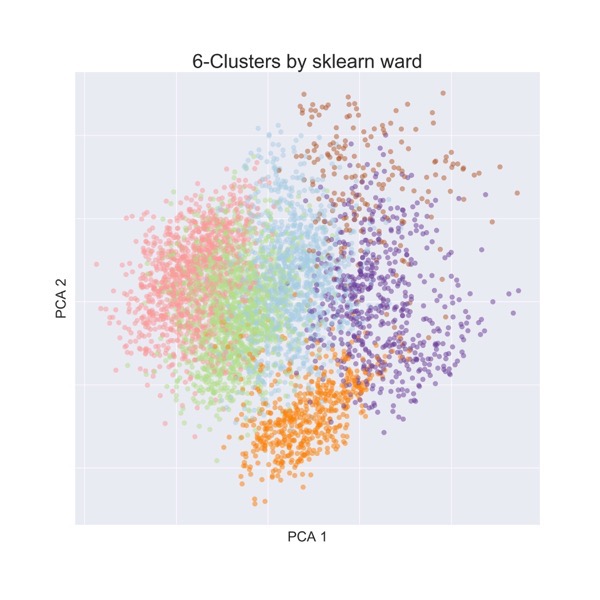
どうでしょう.k平均法による分類の方がウォード法によるクラスタリングよりもよさそうに見えますか?
ここで「よさそう」と判断した理由は,5000 x 5000の距離行列を主成分分析で2次元に可視化した場合に,化合物がうまい具合にわかれているように見えるからです.
本当にそう結論付けてよいでしょうか?
主成分分析における累積寄与率
主成分分析では多次元のデータから情報量の多い軸に対してデータを変換することによって実現されます.次元削減を行う過程で,情報量が多い軸から選択していきます.この過程でもともと情報量の少ない軸に沿ってあった情報は失われます.変換後の軸周りにどの程度の情報があるかを表すものが「寄与率」と呼ばれるものになります.
今回の例では5000次元のデータを2次元にまで落とし込んだ際に失われた情報量を知ることが,クラスタリングがうまくいっているかどうかの判断に重要となります.
scikit-learnのPCAオブジェクトではexplained_variance_ratio_に寄与率が格納されています.下のコードでは「累積寄与率」を求めて,最初の20成分についてプロットしています.
pca_all = PCA()
pca_all.fit(dis_array)
ev_ratio = np.hstack([0, np.cumsum(pca_all.explained_variance_ratio_)])
plt.plot(ev_ratio[:20])
plt.xlim([0,20])
plt.xticks(range(0,20,2))
plt.ylim([0,1.0])
plt.xlabel('n_components')
plt.ylabel('cumulative explained variance')
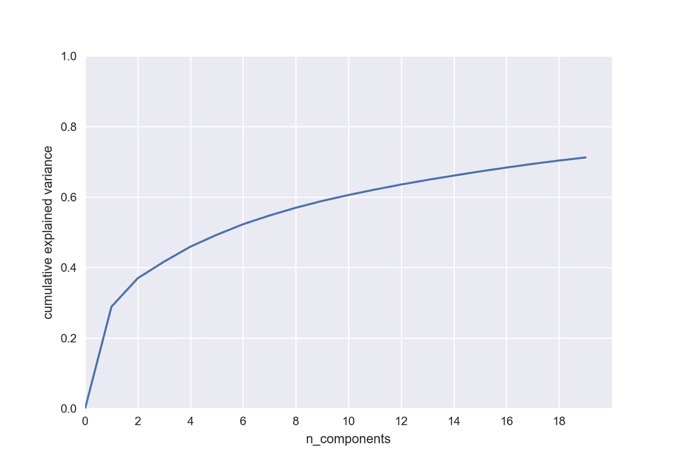
取り入れる主成分の数を増やすことで徐々に累積寄与率が上がっていくのが見てとれます.今回の場合,可視化に用いた最初の2成分では全体の情報量のうち37%ほどしか説明できないことになります.つまり,もしクラスタリングが主に残りの60%の情報を使ってなされたならば,今回の2次元平面上では分かれるはずがないということになります.
主成分分析を行う際には,何らかの判断を下す前に累積寄与率を確認するようにしましょう.
教師なし学習における一般的な注意点
先ほどは主成分分析を行う際の注意点について述べましたが,実は同じようなことが,「次元削減」や「クラスタリング」を含む「教師なし学習」アルゴリズム全般に言えます.
すなわちクラスタリングのような「教師なし学習」では,何をもってアルゴリズムがデータセットをうまく処理できたかを判断する基準があいまいです.実際,我々の目でランダムに選んだ化合物の構造式を見た場合に,分類の「よい」「わるい」を判断するのが難しいと思います.
もっとも様々な研究結果によると,クラスタリングのような多様なライブラリーを構築する方法を用いた方が,ランダムに化合物を選ぶよりもはるかに効率がよいことは示されていますので,その点は安心して大丈夫です.
終わりに
今回は「RDKitとウォード法による化合物の階層型クラスタリング」という話題について,多様性の高いライブラリー構築を目指して,階層型クラスタリング法の1つであるウォード法を用いて化合物のクラスタリングを行いました.具体的には
- 階層型クラスタリングの種類の説明
- pythonの機械学習ライブラリであるscikit-learnを用いたクラスタリングの実行
- scipyを用いたデンドログラムによる可視化
- 主成分分析を行う際の注意点
- 教師なし学習全般に通じる注意点
などに触れることで理解を深めました.
これまでの記事ではRDKitのケモインフォマティクス用ライブラリの側面のみを扱ってきましたが,RDKitは「ケモインフォマティクス・機械学習用ライブラリ」と通常紹介されることからもわかるように,多数の機械学習用アルゴリズムが実装されています.今回扱ったウォード法を用いたクラスタリングも実装されています.
次回はRDKitに実装されている「MaxMin法」を用いることで,多様性の高いライブラリー構築を目指していきたいと思います.
>>次の記事:「RDKitのMaxMin法を用いた多様性の高いライブラリの選定」

コメント