「RDKitのおける記述子の扱い方をリピンスキーのルール・オブ・ファイブを通して学ぶ」という記事では,分子の性質を表現する指標として記述子(デスクリプター)について説明し,RDKitを用いて実際に計算を行ってみました.その際に扱った記述子は分子量や水素結合ドナーの数など,2次元の構造式をもとに算出が可能なものばかりでした.
近年では分子の立体的な特徴を表現することがますます重要になっています.既にいくつもの3次元記述子が提案されていますが,今回はその中からよく使われているものでRDKitに実装されている
- Fsp3
- PMI
- PBF
の3つを紹介します.
ライブラリのインポートと分子の準備
まずは必要なライブラリをimportし,分子を準備します.今回も「Platinum dataset」を使って分析を行うことにしましょう.
# ライブラリのimport
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from rdkit import rdBase, Chem
print(rdBase.rdkitVersion) # 2020.09.3
from rdkit.Chem import AllChem, Descriptors, Descriptors3D, rdMolDescriptors
# 分子の読み込み
suppl = Chem.SDMolSupplier('./SDF/platinum_dataset_2017_01.sdf')
mols = [x for x in suppl if x is not None]
len(mols) # 4548
Fsp3は分子の複雑さの指標
または
Chem.rdMolDescriptors.CalcFractionCSP3(mol)
Chem.AllChem.CalcFractionCSP3(mol)
ジメチルピリジンとその不飽和型化合物のジメチルピペリジンでは一体どれほどに異性体が存在しうるでしょうか?答えは前者の6種に対し,後者は光学異性体も含めると30種も存在します.両者の分子量はほとんど変わらないことから,芳香族が脂肪族に変わることで分子はその複雑さを増し,化合物がカバー可能なケミカルスペースが大幅に拡がったことになります.
2009年にLoveringらは,開発化合物の進捗段階とその構造を調べていくうちに,化合物の複雑さを示す指標として全炭素におけるsp3炭素の割合(Fsp3)という記述子の重要性を提唱しました.もちろん天然物由来の医薬品は多いですし,天然物らしさを現す指標として不斉炭素の割合が挙げられることも知られていましたので,彼らの考えが特段新しいわけではありませんでした.
それでも「Flatland」というキャッチーなフレーズと,簡単に算出できる記述子を用いていたことから,ライブラリーの多様性を考える上で重要な指標へと一挙に駆け上がりました.近年ではアカデミアにおいて反応開発を行う上でも重要視されつつあり,有機合成化学者からの引用も増加傾向です.
なおFsp3自体は構造式から数えるだけで算出可能ですので,立体構造を必要とする「3次元記述子」ではありませんが,化合物の立体性を考える上で大切な指標なので,ここで扱っています.
下のコードではプラチナデータセット中のFsp3の値を度数分布表にまとめています.
flat = [Descriptors.FractionCSP3(mol) for mol in mols] bins = [0,0.2,0.4,0.6,0.8,1.0] pd.value_counts(pd.cut(flat, bins), sort=False)
| 階級 | 度数 |
|---|---|
| (0.0, 0.2] | 1064 |
| (0.2, 0.4] | 1420 |
| (0.4, 0.6] | 969 |
| (0.6, 0.8] | 362 |
| (0.8, 1.0] | 341 |
PMIプロットで分子の形を可視化する
Chem.Descriptors3D.NPR2(mol)
または
Chem.rdMolDescriptors.CalcNPR1(mol)
Chem.rdMolDescriptors.CalcNPR1(mol)
Chem.AllChem.CalcNPR1(mol)
Chem.AllChem.CalcNPR1(mol)
学会や論文などで最も目にするのがここで紹介するPMIプロットと呼ばれるものかもしれません.分子の形をdisk/rod/sphereで特徴付けて三角形内のどこにライブラリーが分布するかを表す図をよく見かけます.
PMIプロットは主慣性モーメント3成分のうち最大のもので除した,規格化された(normalized)値をx-y平面にプロットしたものになります.NPR1が0から1の間,NPR2は0.5から1の間に収まります.従って分布がプロットされる三角形は正三角形のように描いてあることが多いですが,実は縦に引き延ばしているわけです.
なお主慣性モーメント自体もDescriptors3D.PMI1やrdMolDescriptors.CalcPMI1などによって得ることが可能ですが,必要になる場合は少ないでしょう.
下のコードでは実際にPMIプロットを作成して,化合物の散布図を描いてみます.また対照化合物として,ベンゼン(disk化合物),アセチレン(rod化合物),アダマンタン(sphere化合物)もプロットしてあります.
# reference molecules
benzene = AllChem.AddHs(Chem.MolFromSmiles('c1ccccc1'))
acetylene = AllChem.AddHs(Chem.MolFromSmiles('C#C'))
adamantane = AllChem.AddHs(Chem.MolFromSmiles('C1C2CC3CC1CC(C2)C3'))
AllChem.EmbedMolecule(benzene, AllChem.ETKDGv3())
AllChem.EmbedMolecule(acetylene, AllChem.ETKDGv3())
AllChem.EmbedMolecule(adamantane, AllChem.ETKDGv3())
benzene = AllChem.RemoveHs(benzene)
acetylene = AllChem.RemoveHs(acetylene)
adamantane = AllChem.RemoveHs(adamantane)
ben_x, ben_y = Descriptors3D.NPR1(benzene), Descriptors3D.NPR2(benzene)
alkyne_x, alkyne_y = Descriptors3D.NPR1(acetylene), Descriptors3D.NPR2(acetylene)
adam_x, adam_y = Descriptors3D.NPR1(adamantane), Descriptors3D.NPR2(adamantane)
# plot
x = []
y = []
for m in mols:
x.append(Descriptors3D.NPR1(m))
y.append(Descriptors3D.NPR2(m))
xx = np.linspace(0,1,100)
plt.plot(x, y, 'o', ms=4)
plt.plot(ben_x, ben_y, 'ks', ms=10)
plt.plot(alkyne_x, alkyne_y, 'ks', ms=10)
plt.plot(adam_x, adam_y, 'ks', ms=10)
plt.plot(xx, 1-xx, 'r', alpha=0.4)
plt.plot(xx, np.ones(100), 'r', alpha=0.4)
plt.plot(xx, xx, 'r', alpha=0.4)
plt.xlabel('NPR1')
plt.ylabel('NPR2')
plt.xlim(-0.01,1.005)
plt.ylim(0.5,1.005)
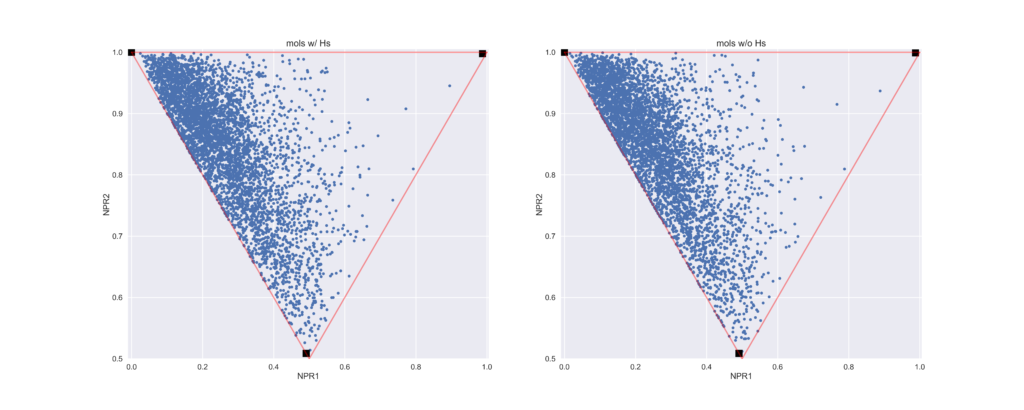
今回のコードでは水素原子を除いた状態で計算しています.下のプロットでは参考までに
- 左:水素有りの状態で計算したもの
- 右:水素を除いた構造で計算したもの
の2つを示しています.ややわかりにくいかもしれませんが,水素の有無で値が変わっているのが見て取れると思います.
PBFは平面からの逸脱度によって分子の3次元性を表現する新しい記述子
「Plane of Best Fit(PBF)」は2012年に発表された,分子がどれだけ平面から乖離しているかを表す比較的新しい記述子です.この記述子ではまず水素を除く原子の座標に対して最小二乗法を用いて平面を作成します.そしてその平面と各原子がどの程度離れているかを表したものがPBFになります.
定義からPBFは0以上無限大まで取りえますが,大規模データセットによる検証から,
- 低分子で大体2以下
- プロテインなどの高分子でも10以下
にほとんどの場合収まることが示されています.また定義よりPBFは水素の有無で値は変わりません.
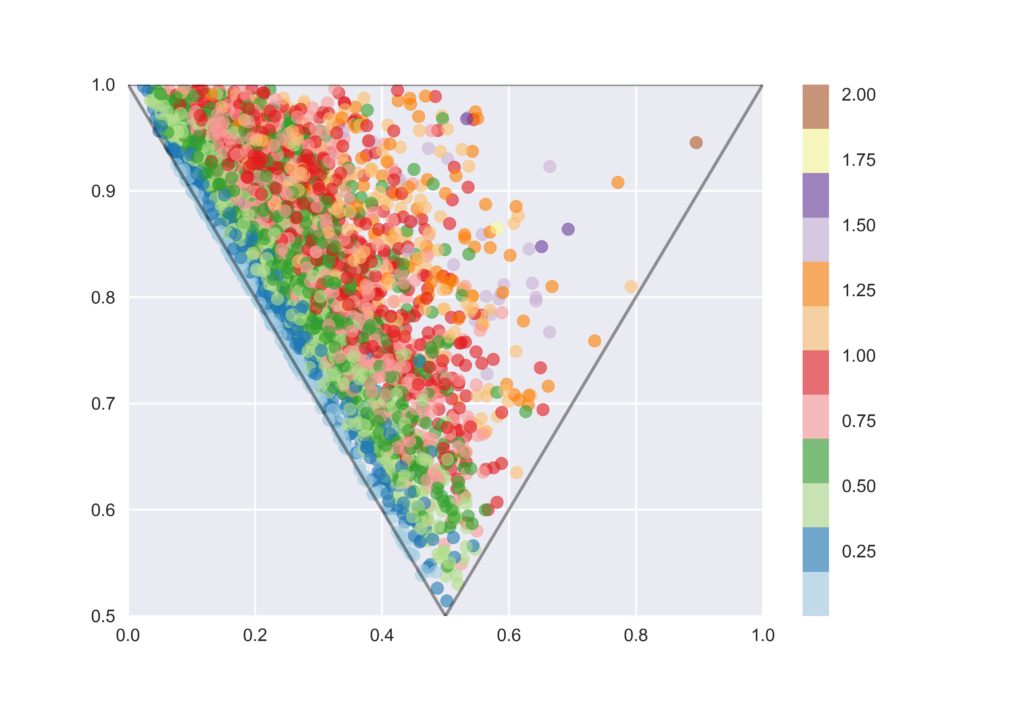
下記のコードではPBFの値を求めた後に,上記のPMIプロットに対してカラーマップでPBFを適用しています.類似のプロットが元文献にあったのですが,PBFが小さいものはほとんどがrodとdiskの間に分布しており,かなりきれいに識別できていることが伺えると思います.
pbf = []
for mol in mols:
pbf.append(rdMolDescriptors.CalcPBF(mol))
s2 = pd.Series(pbf)
s2.describe().round(2)
plt.scatter(x, y, vmin=min(pbf), vmax=max(pbf), c=pbf, cmap='Paired', alpha=0.6)
plt.plot(xx, 1-xx, 'k', alpha=0.4)
plt.plot(xx, np.ones(100), 'k', alpha=0.4)
plt.plot(xx, xx, 'k', alpha=0.4)
plt.colorbar()
plt.xlim(0,1)
plt.ylim(0.5,1)
| PBF | |
|---|---|
| count | 4548.00 |
| mean | 0.64 |
| std | 0.28 |
| min | 0.00 |
| 25% | 0.45 |
| 50% | 0.64 |
| 75% | 0.83 |
| max | 2.04 |
終わりに
今回は分子の立体的な特徴を表現する記述子として,Fsp3,PMI,PBFの3つを扱いました.何れもよくみかける指標だと思いますのでしっかり理解し,今後のデータ分析に役立てていきましょう.
化学者が「化合物が似ている・異なる」という場合には,実際に構造を目で見ることで判断していると思います.それではコンピュータに判断させるためにはどうしたらよいでしょうか?
次回は化合物の類似度をコンピュータが比較するために基準となる「フィンガープリント」と呼ばれるものを解説していきたいと思います.段々と内容が複雑になってきていますが,できること・応用範囲も広がってきています.頑張っていきましょう.
>>次の記事:「RDKitでフィンガープリントを使った分子類似性の判定」

コメント
お世話様です。「PBFの値を求めた後に,上記のPMIプロットに対してカラーマップでPBFを適用」のコードを実行すると、
plt.scatter(x_h, y_h, vmin=min(pbf), vmax=max(pbf), c=pbf, cmap=’Paired’, alpha=0.6)
のところで、NameError: name ‘x_h’ is not defined となります。ご多用中、誠に恐縮ですが、当方がチェックすべき箇所等を教えて頂けますか。
コメントありがとうございます.
PMIプロットの説明のところで,「水素の有無で値が(やや)変わる」ことに軽く言及しました.今回エラーが出ている「x_h」と「y_h」は,この説明のために用意した変数ですが,本文のコード中には記載がありませんでしたので,そのまま貼り付けるとエラーになる状態でした.コードは修正しておきました.ご指摘ありがとうございます.
水素を付与した分子を用いてCalcNPR1/2を行う際には,SDF読み込みの際に「removeHs=False」オプションを付けた上で分子を構築し,計算を実行してみてください.なお本文中でも言及しましたが,「PBF自体は水素の有無で不変」です.
今後ともよろしくお願いいたします.