ケモインフォマティクスにおけるモデル構築は
- 分子を特徴ベクトルへと変換する(encoding)
- 特徴ベクトルと目的とする分子の性質との関係を記述する(mapping)
という2段階に分けられます.
本サイトではこれまでケモインフォマティクス用ライブラリーのRDKitを用いて,第1段階であるどのように分子の構造情報を表現するかについて,「RDKitでケモインフォマティクスに入門」という記事から順番に解説していきました.
今回からは第2段階目として,分子より得られた構造情報を入力として現象を予測するモデルの構築について学びます.今回の題材としては「Ames試験の結果(陰性・陽性)を予想」することとし,機械学習の中でも特にクラス分類問題といわれるものについて学びます.
「Benchmark Data Set for in Silico Prediction of Ames Mutagenicity」J. Chem. Inf. Model. 2009, 49, 2077. (DOI: 10.1021/ci900161g)
機械学習の分類
機械学習は膨大な内容を含む分野ですが,ここでは基礎的な事柄についてまとめておきます.
教師あり学習と教師なし学習
入力情報とペアになった出力(正解)を与えてモデルを構築する問題を「教師あり学習」といいます.今回行う変異原性の予測も「陰性」「陽性」という正解が与えられていますので,こちらになります.
一方で,正解の与えられていない問題を「教師なし学習」といいます.例えば,「RDKitとk平均法による化合物の非階層型クラスタリング」という記事で扱ったクラスタリングや主成分分析などが挙げられます.
回帰と分類
教師あり学習のうち,連続データの予測を行うものを「回帰」といいます.例えば活性値(IC50など)を予測するモデルは回帰になります.
一方でデータをいくつかのクラスに分けるものを「分類」と呼びます.今回扱う問題では,化合物を「陰性」と「陽性」に分類するので,2クラス分類問題(binary classification)になります.クラスタリングではいくつに分けるかもわかっていませんが,分類問題では何クラスにわけるかは知らされているのが異なります.
分類を行う機械学習の手法はいくつか存在しますが,今回はその中でも「k-最近傍法(k-nearest neighbors)」と呼ばれるものを扱います.実装はpythonの機械学習用のライブラリーであるscikit-learnのものを用います.
k-最近傍法とは
k-最近傍法は最も単純な学習アルゴリズムと言われます.具体的には
- データセットを特徴量空間に配置する(学習)
- k個の近接データポイントの値から新しい点の値を定める(予測)
といった2段階で行われます.
具体例として,下図のように赤と青の点が配置された平面において,黒い点が赤青どちらに分類されるかを考えてみます.
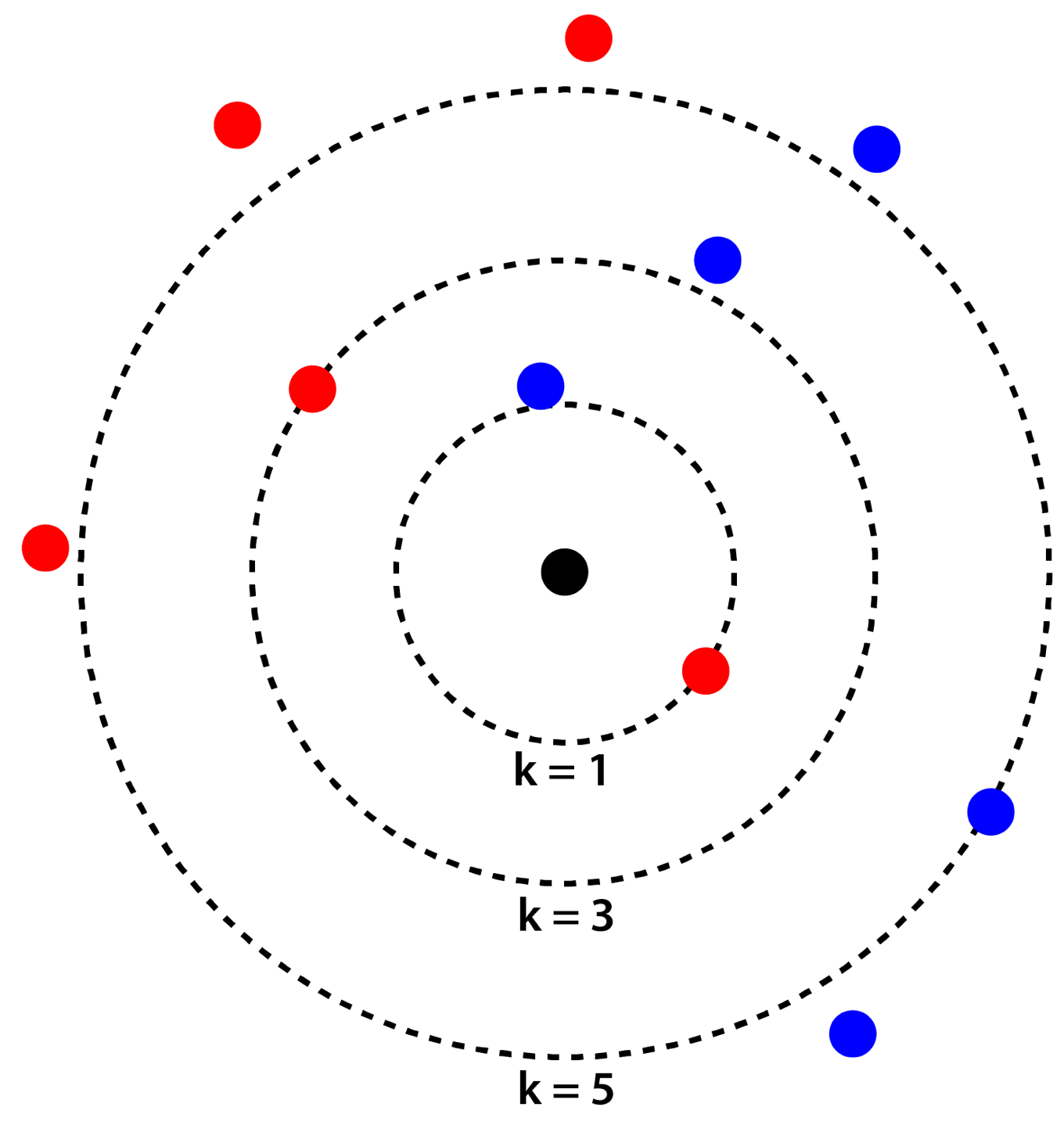
- k=1の場合:最も近い距離にある赤い点と同じく「赤」に分類されます.
- k=3の場合:最も近い3つの点は赤2青1ですので,多数決により「赤」に分類されます.
- k=5の場合:最も近い5つの点は赤2青3ですので,多数決により「青」に分類されます.
このようにkの値を変えることで結果が変わってきますので,kの値がk-最近傍法における最も重要なパラメータになります.
またどのような「距離」を用いるかに興味のある方もいるかと思われますが,通常はデフォルト設定の「ユークリッド距離」で十分です.
用いるデータセットについて
今回利用する「Benchmark Data Set for in Silico Prediction of Ames Mutagenicity」という論文では,変異原性性試験として最も用いられているAmes試験の結果を集めたものが付属しています.
Ames試験とは
変異原性試験として広く実施されている試験になります.実験ではヒスチジン要求株の原核生物をヒスチジン欠損培地に蒔きます.これらの株は生存に必須のヒスチジンを欠くために通常は生育しませんが,何らかの原因によりヒスチジンを合成可能になることがあります.そのため増えたコロニーを観察することで,化合物の変異原性を評価できます.
こういった変異原性は医薬品開発にとっては致命的ですので,前もってどの化合物が陽性になりそうか判定することができれば非常に有用になります.構造と変異原性の関係を記述するモデルの構築研究は盛んに行われています.
RDKitとscikit-learnを使ったモデル構築
それではRDKitとscikit-learnを用いて具体的な方法を見ていきましょう.
分子の読み込み
論文のデータはタブ区切りのテキストファイルで,「SMILES」「CAS NO」「変異原性」の3つのデータが6512化合物について格納されています.
以下のコードでは
- 必要なライブラリのインポート
- pandasのデータフレームとして情報を読み込む
- SMILESからRDKitのMOLオブジェクトを構築
- 読み込めないSMILESを含むデータを除去
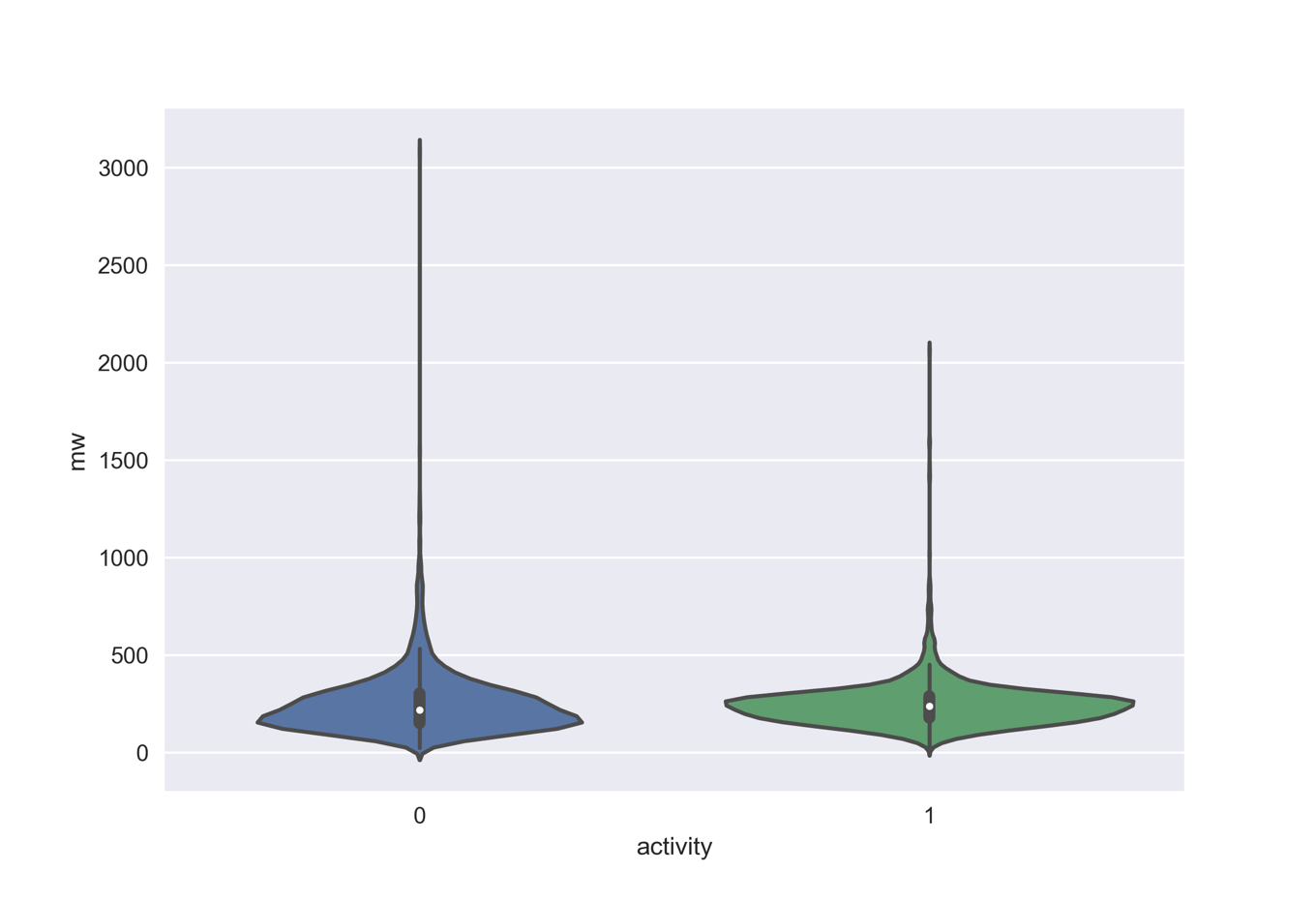
- データを眺めるために,分子量分布を変異原性の有無についてプロット
という順番で処理を行っています.6512分子のうち6506分子の読み込みに成功し,そのうち陽性(activity=1)が3497分子,陰性(activity=0)が3009分子でした.
## 1. ライブラリのインポート
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, Descriptors
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
print(rdBase.rdkitVersion) # 2018.03.3
## 2. 分子の読み込み
df = pd.read_csv('ci900161g_si_001/smiles_cas_N6512.smi', sep='\t', header=None)
df.columns = ['smiles', 'CAS_NO', 'activity']
len(df) # 6512
## 3. MOLオブジェクト構築
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='smiles')
## 4. 読み込めない分子の削除
df['MOL'] = df.ROMol.map(lambda x: False if x == None else True)
del_index = df[ df.MOL == False ].index
df2 = df.drop(del_index)
len(df2) # 6506
len(df2[df2.activity == 0]), len(df2[df2.activity == 1])
(3009, 3497)
## 5. 分子量分布をプロット
df2['mw'] = df2.ROMol.map(Descriptors.MolWt)
sns.violinplot(x='activity', y='mw', data=df2)
入力ベクトルとしてフィンガープリントを準備
今回は入力情報として分子のフィンガープリントを用いることにします.モルガンフィンガープリントとMACCS Keyの2つを用いることで,入力情報がモデルの精度に与える影響を見ることにします.
scikit-learnの入力ベクトルとしては(サンプル数 x 特徴量数)という形のnumpy arrayを用意する必要があります.また出力ラベルは(サンプル数,)です.下記のコードを確認してみてください.
## モルガンフィンガープリント
morgan_fp = []
for mol in df2.ROMol:
fp = [i for i in AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)]
morgan_fp.append(fp)
morgan_fp = np.array(morgan_fp)
morgan_fp.shape # (6506, 2048)
## MACCS Keys
maccskeys = []
for mol in df2.ROMol:
maccskey = [i for i in AllChem.GetMACCSKeysFingerprint(mol)]
maccskeys.append(maccskey)
maccskeys = np.array(maccskeys)
maccskeys.shape # (6506, 167)
## 出力ラベル
target = df2.activity
target.shape # (6506,)
scikit-learnでのモデル構築
sklearn.neighbors.KNeighborsClassifier(n_neighbors)
訓練データとテストデータ
機械学習モデルの目的は未知のデータに対してよい精度を出すことです.もし手持ちのデータ全て使ってモデル構築をしてしまうと,そのデータ特有の情報も入れ込んで構築されたモデルができあがってしまい,逆に未知データに対する精度が下がってしまいます.これを「過剰適合(overfitting)」といいます.
そのために手持ちデータの一部をモデル検証用に残しておくことが行われます.モデル構築には使われなかったテスト用データで高い精度を出せるモデルがよいものになります.
scikit-learnでは手持ちのデータを学習用とテスト用に分けるメソッドtrain_test_splitが用意されています.標準設定では75%を学習用に,残り25%をテスト用へと分割します.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(morgan_fp, target, random_state=0) X_train.shape, X_test.shape, y_train.shape, y_test.shape ## ((4879, 2048), (1627, 2048), (4879,), (1627,))
scikit-learnでのk-最近傍法の実装
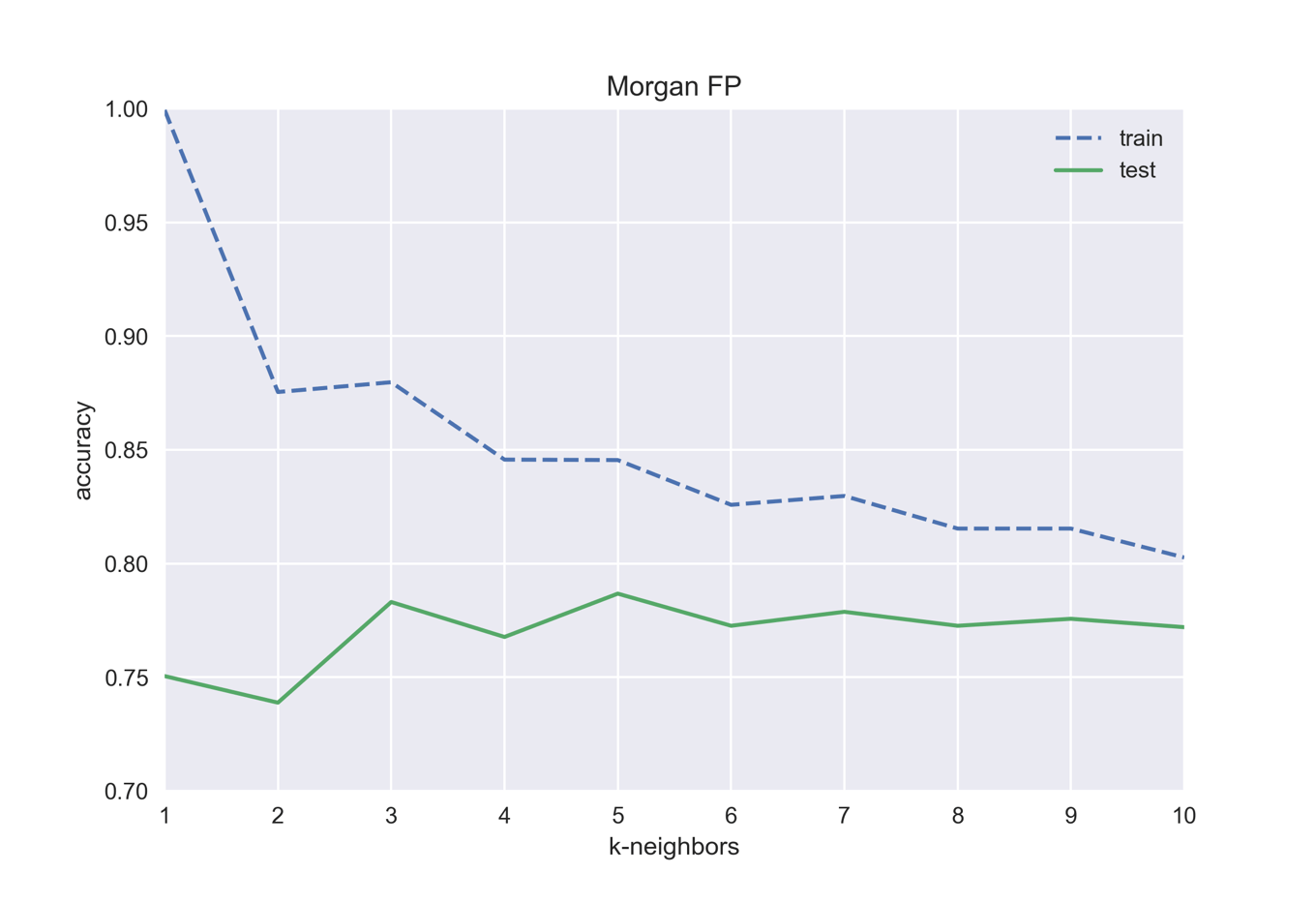
k-最近傍法では「考慮する近傍点の数k」が変数になります.下の例ではkを1から10に変化させていき,各々について訓練データとテストデータの精度を比べています.同じ入力データでもkを変えることで精度が変わることを確認しましょう.
from sklearn.neighbors import KNeighborsClassifier
morgan_train_acc = []
morgan_test_acc = []
for i in range(1,11):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train, y_train)
train_acc = knn.score(X_train, y_train)
test_acc = knn.score(X_test, y_test)
print('test accuracy with k={}: {:.3f}'.format(i, test_acc))
morgan_train_acc.append(train_acc)
morgan_test_acc.append(test_acc)
test accuracy with k=1: 0.750 test accuracy with k=2: 0.739 test accuracy with k=3: 0.783 test accuracy with k=4: 0.768 test accuracy with k=5: 0.787 test accuracy with k=6: 0.773 test accuracy with k=7: 0.779 test accuracy with k=8: 0.773 test accuracy with k=9: 0.776 test accuracy with k=10: 0.772
k=1では訓練データに対する精度は完璧ですが,テスト用データの精度は低く過剰適合を起こしています.この場合はテスト用データの精度が最も高い「k=5」がよいモデルです.
下のコードでは同じことをMACCS Keysを用いて行っています.同じkの値でも,フィンガープリントの種類が異なると精度が異なることを確認しましょう.
X2_train, X2_test, y2_train, y2_test = train_test_split(maccskeys, target, random_state=0)
maccs_train_acc = []
maccs_test_acc = []
for i in range(1,11):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X2_train, y2_train)
train_acc = knn.score(X2_train, y2_train)
test_acc = knn.score(X2_test, y2_test)
print('test accuracy with k={}: {:.3f}'.format(i, test_acc))
maccs_train_acc.append(train_acc)
maccs_test_acc.append(test_acc)
test accuracy with k=1: 0.768 test accuracy with k=2: 0.763 test accuracy with k=3: 0.781 test accuracy with k=4: 0.774 test accuracy with k=5: 0.773 test accuracy with k=6: 0.774 test accuracy with k=7: 0.778 test accuracy with k=8: 0.779 test accuracy with k=9: 0.780 test accuracy with k=10: 0.778
この場合はk=3が一番よさそうです.
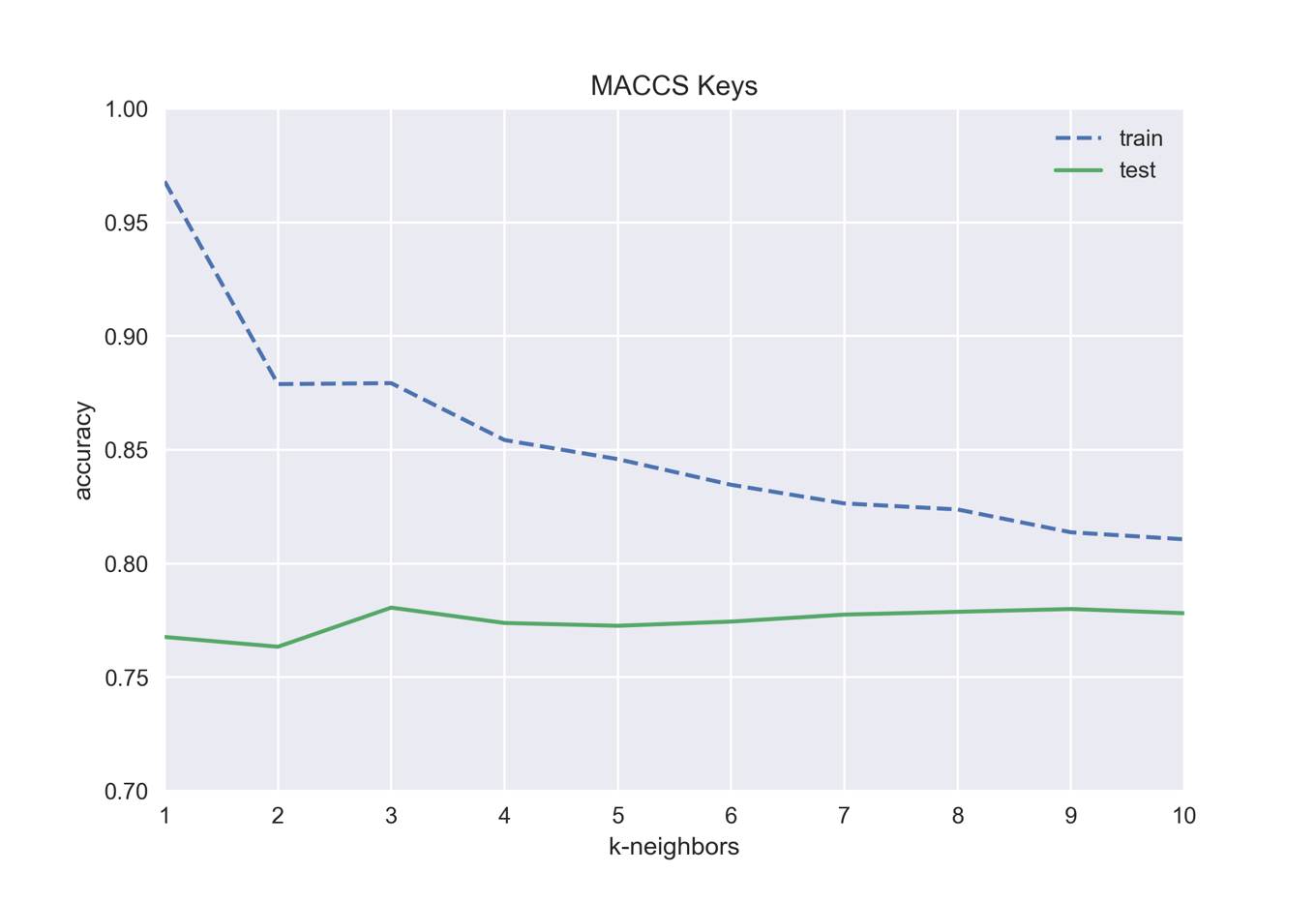
モルガンフィンガープリント,及びMACCS Keysについて検証を行ってきましたが,いずれの場合も精度は0.8止まりでした.これはk-最近傍法がフィンガープリントのような
- 特徴量の数が多く(数百以上)
- 多くの特徴量がゼロ(疎なデータ)
といったデータに対してはうまく機能しないためです.また特徴量数が多くなるとテストセットの予測も非常に遅くなります.
こういった特徴から, k-最近傍法は他の手法を試す前の検証目的で用いることが多いです.
終わりに
今回は「RDKitとscikit-learnで機械学習:変異原性をk-最近傍法で予測」という話題について,
- 教師あり学習と教師なし学習
- 回帰と分類
- RDKitとscikit-learnを用いたモデル構築
などについて触れました.特にモデル構築においては,
- どのように分子の情報を入力ベクトルとして表現するかで同じ機械学習手法を用いても精度が変わること
- 訓練データについて精度が高いモデルが必ずしもテストデータでよい精度を上げるわけではないこと(過剰適合)
を確認しました.
今後はk-最近傍法以外の手法について学ぶとともに,どのようにモデルを最適化していくかについて交差検証とグリッドサーチについても見ていきたいと思います.次回は「決定木」と呼ばれる手法について学んでいきましょう.
>>次の記事:「scikit-learnの決定木でAmes試験データセットを機械学習」
コメント