これまでAmes試験と呼ばれるテストの結果を用いて,化合物の変異原性の有無を予測する機械学習モデルを構築してきました.
- 「RDKitとscikit-learnで機械学習:変異原性をk-最近傍法で予測」ではk-最近傍法
- 「scikit-learnの決定木でAmes試験データセットを機械学習」では決定木
- 「RDKitでランダムフォレスト:機械学習でも「みんなの意見」は案外正しい」ではランダムフォレスト
といった記事で見てきたように,同じデータセットでも用いるアルゴリズムを変えることによって精度が異なりました.この場合の「精度」とは,scikit-learnのscoreメソッドでデフォルト設定になっている「正しく予測ができた化合物の割合」になります.
今回はモデルの判断基準として精度のさまざまなものを扱い,モデルの利用目的に応じて最適なものを選ぶことができるようにしたいと思います.
「Benchmark Data Set for in Silico Prediction of Ames Mutagenicity」J. Chem. Inf. Model. 2009, 49, 2077. (DOI: 10.1021/ci900161g)
分子の準備
実際に説明を始める前に必要なライブラリーのimportと分子の読み込みを行います.
これまでと同様に以下のコードでは
- 必要なライブラリのインポート
- pandasのデータフレームとして情報を読み込む
- SMILESからRDKitのMOLオブジェクトを構築
- 読み込めないSMILESを含むデータを除去
- 分子フィンガープリントの準備
- データを訓練用データとテスト用に分割
という順番で処理を行っています.
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, PandasTools
print(rdBase.rdkitVersion) ## 2018.09.1
mpl.style.use('seaborn')
df = pd.read_csv('./ci900161g_si_001/smiles_cas_N6512.smi', sep='\t', header=None)
df.columns = ['smiles', 'CAS_NO', 'activity']
PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='smiles')
df['MOL'] = df.ROMol.map(lambda x: False if x == None else True)
del_index = df[ df.MOL == False].index
df2 = df.drop(del_index)
fps = []
for mol in df2.ROMol:
fp = [x for x in AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)]
fps.append(fp)
fps = np.array(fps)
fps.shape # (6506, 2048)
targets = df2.activity
targets.shape # (6506,)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(fps, targets, random_state=0)
エラーの種類
陰性の化合物を陽性と判断してしまう「偽陽性」(false positive)と,陽性の化合物を陰性と判断してしまう「偽陰性」(false negative)を考えてみましょう.研究プロジェクトにおいて,変異原性を有する(陽性)化合物が弾かれずに研究段階が進んでしまうと莫大な投資が無駄になってしまうことになりますので,今回モデル構築の対象としているような変異原性試験では,「偽陰性」をできるだけ少なくすることが望ましいです.
このように2つのエラーが等価でない場合にはどのようにモデルを評価するのが好ましいでしょうか?
混同行列
今回のような2クラス分類の結果を表現する方法として「混同行列」(confusion matrix)と呼ばれるものがあります.先ほどみた「偽陽性(FP)」「偽陰性(FN)」に加えて,陽性の化合物を正しく判定できた「真陽性」(true positive; TP)と,陰性のものを正しく判定できた「真陰性」(true negative; TN)を考えてみましょう.この4成分で全ての場合をカバーできます.
混同行列ではこれら4個の成分を下のような2×2の行列に割り当てます.各行が実際のクラスに相当し,各列がモデルの予測に相当します.対角成分が正しく予測できた数になります.混同行列を眺めることで,モデルがどのように本来のクラスと「混同」して,間違ったクラスを割り当てているかがわかります.
| 「陰性」と判定 | 「陽性」と判定 | |
|---|---|---|
| 陰性クラス | TN | FP |
| 陽性クラス | FN | TP |
混同行列はscikit-learnではmetrics.confusion_matrixに実装されています.下のコードではランダムフォレストを用いて,5-分割交差検証によって混同行列を出力しています.
from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import confusion_matrix from sklearn.model_selection import cross_val_predict forest = RandomForestClassifier(n_estimators=5000, n_jobs=-1) cv_predict = cross_val_predict(forest, X_train, y_train, cv=5) confusion_matrix(y_train, cv_predict)
array([[1781, 472],
[ 481, 2145]])
このようにして得られた混同行列から,モデルを評価する様々な指標が算出できます.よく使われるものをいくつか見ていきたいと思います.
精度
精度(accuracy)は全てのデータのうち,正確に判定できたデータの割合です.scikit-learnのscoreメソッドで評価されるデフォルトの基準になっています.
$$ accuracy = \frac{TP + TN}{TP + TN + FP + FN} $$
適合率
適合率(precision)は,「陽性」と判定された化合物のうち,実際に陽性であった割合になります.偽陽性をあまり起こさないモデルが好ましいときに用いられる評価基準になります.
$$ precision = \frac{TP}{TP + FP} $$
再現率
再現率(recall)は実際に陽性のデータのうち,「陽性」と判定されたものの割合になります.偽陰性をできるだけ減らしたい場合に有用な評価基準になります.再現率は感度(sensivity),真陽性率(true positive rate; TRP)などとも呼ばれます.
$$ recall = \frac{TP}{TP + FN} $$
F1-値
適合率は偽陽性が少ないモデルが好ましいことから,確実に陽性と自信を持てるものだけを陽性として残りは陰性と判断するような,「慎重なモデル」が評価が高くなりがちです.
一方で再現率は偽陰性が少ないモデルが好ましいため,多少自信がなくても陽性と判断するような,「疑わしきは罰するタイプのモデル」の評価が高くなりがちになります.
このように適合率と再現率では傾向が異なりますので,2つの指標を合わせたF-値と呼ばれる判断基準が存在します.特に適合率と再現率の調和平均がF1-値と呼ばれるものになります.
$$ F_1 = \frac{2}{\frac{1}{適合率} + \frac{1}{再現率}} = 2 \times \frac{適合率 \times 再現率}{適合率 + 再現率} $$
scikit-learnでの評価基準
sklearn.metrics.precision_score(label, predicted_label)
sklearn.metrics.recall_score(label, predicted_label)
sklearn.metrics.f1_score(label, predicted_label)
精度(accuracy),適合率(precision),再現率(recall),F1-値はscikit-learnでは全てmetrics.confusion_matrixに実装されています.
from sklearn.metrics import accuracy_score, recall_score, f1_score, precision_score
print('accuracy: {:.3f}'.format(accuracy_score(y_train, cv_predict)))
print('precision: {:.3f}'.format(precision_score(y_train, cv_predict)))
print('recall: {:.3f}'.format(recall_score(y_train, cv_predict)))
print('F1-score: {:.3f}'.format(f1_score(y_train, cv_predict)))
accuracy: 0.805 precision: 0.820 recall: 0.817 F1-score: 0.818
適合率-再現率カーブ
モデルが「データをどれくらいの確度で判断しているか」という程度によって,適合率や再現率は変わってきます.すなわち,同じモデルでも判断を下す「閾値」を変えることで適合率や再現率を調整可能です.これを適合率と再現率のトレードオフと呼びます.
scikit-learnのprecision_recall_curveメソッドでは,モデルがどの程度の確度を持って予想しているかを与えることで,閾値を変えながら適合率と再現率を計算します.
まずはランダムフォレストを用いた交差検証の結果で,method=’predict_proba’オプションを設定することでモデルが予測する確率返すようにします.
cv_proba = cross_val_predict(forest, X_train, y_train, cv=5, method='predict_proba') cv_proba[:5]
array([[0.2258, 0.7742],
[0.0856, 0.9144],
[0.3014, 0.6986],
[0.4904, 0.5096],
[0.0374, 0.9626]])
得られる確率は「陰性(0)である確率」「陽性(1)である確率」のリストのリストですので,このうち陽性である確率のリストのみを取得して,precision_recall_curveメソッドに渡します.
forest_proba = cv_proba[:,1]
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train, forest_proba)
plt.plot(thresholds, precisions[:-1], label='Precision')
plt.plot(thresholds, recalls[:-1], label='Recall')
plt.xlabel('Threshhold')
plt.xlim(0,1)
plt.ylim(0,1)
plt.legend()
閾値を変えることで適合率と再現率がどのように変化するかがわかります.
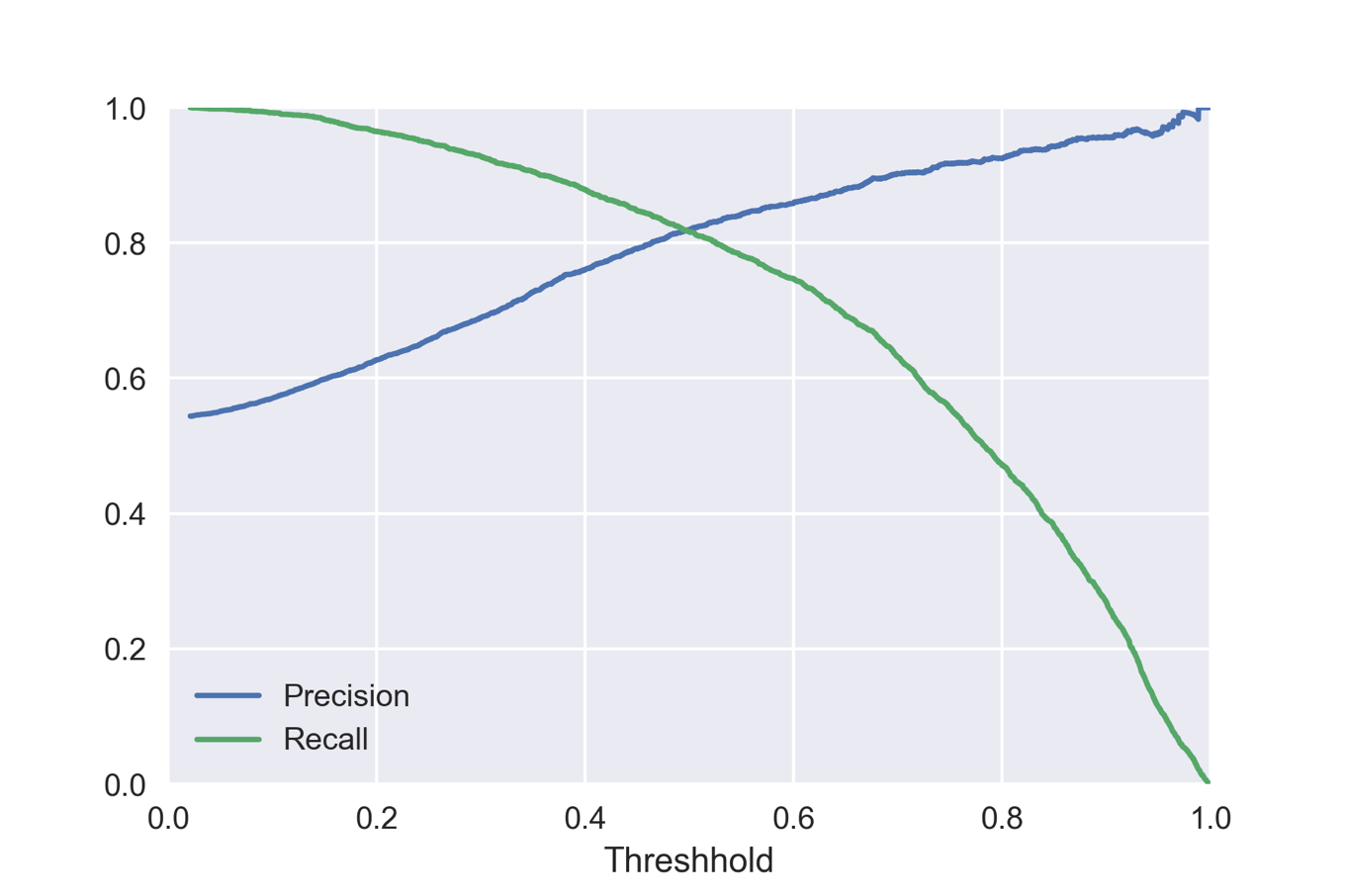
横軸に再現率,縦軸に適合率を設定してプロットしたものが下図になります.縦横軸が逆転しているものもよく見かけます.いずれにせよ,この適合率-再現率カーブはモデル評価によく使われるものになります.
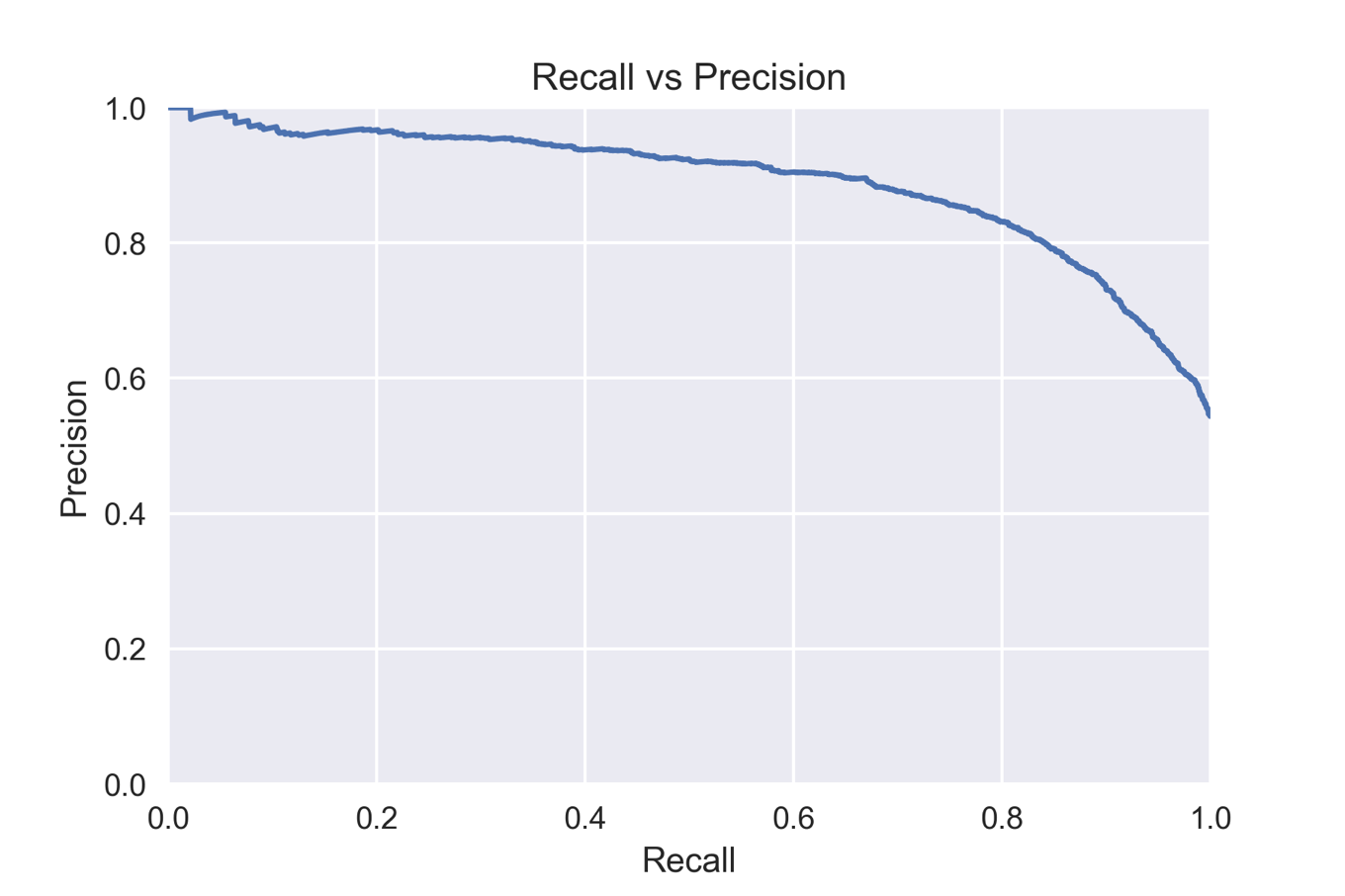
ROCカーブ
適合率-再現率カーブと並んで,さまざまな閾値に対してモデルを評価する方法としてよく使われるものに受信者動作特性(receiver operating characteristics; ROC)カーブと呼ばれるものがあります.
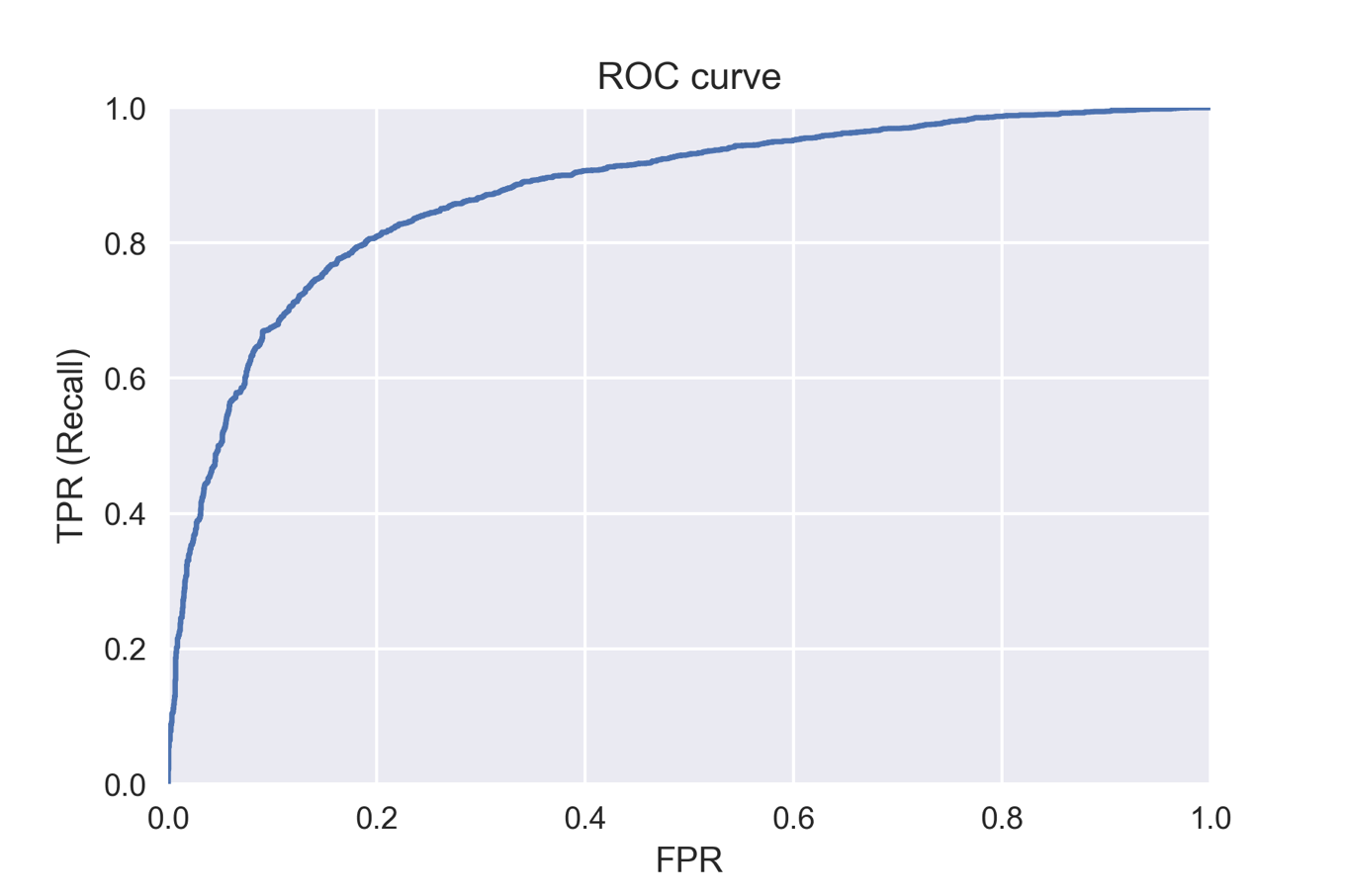
ROCカーブは横軸に偽陽性率(FPR),縦軸に真陽性率(TPR)を設定してプロットしたものです.scikit-learnではroc_curveとして実装されています.
from sklearn.metrics import roc_curve
fprs, tprs, thresholds = roc_curve(y_train, forest_proba)
plt.plot(fprs, tprs)
plt.xlim(0,1)
plt.ylim(0,1)
plt.xlabel('FPR')
plt.ylabel('TPR (Recall)')
plt.title('ROC curve')
ROCカーブでは左上に近づくほどよいモデルと言えます.
AUCによる要約方法
sklearn.metrics.roc_auc_score(label, confidence)
適合率-再現率カーブやROCカーブを眺めることでもさまざまなことがわかりますが,これらのカーブに含まれている情報を要約することができると便利です.そのための方法が,カーブ下の面積(area under the curve; AUC)を求める方法で,それぞれaverage_precision_scoreメソッドとroc_auc_scoreメソッドで求めることができます.
from sklearn.metrics import average_precision_score,
print('Average precision: {:.3f}'.format(average_precision_score(y_train, forest_proba)))
print('ROC-AUC: {:.3f}'.format(roc_auc_score(y_train, forest_proba)))
Average precision: 0.889 ROC-AUC: 0.874
scikit-learnの評価基準を変更して交差検証
先にも述べたように,変異原性試験では偽陰性をなるべく減らしたいので,評価基準をROC-AUCとするのが好ましいです.scikit-learnではscoringオプションを設定することで評価基準をデフォルトの精度から他のものへと変更することが可能です.
下のコードでは交差検証の基準にROC-AUCを用いています.
from sklearn.model_selection import cross_val_score cv_results_roc = cross_val_score(forest, X_train, y_train, cv=5, scoring='roc_auc') cv_results_roc
array([0.88555639, 0.8795671 , 0.87004963, 0.86473016, 0.87393016])
終わりに
今回は「機械学習モデルの評価方法:化合物の変異原性の有無を題材に」という話題について,
- 混同行列とそこから導かれる評価基準について
- 適合率-再現率カーブとROCカーブについて
- scikit-learnを用いた各種評価基準の使い方
などについて学んできました.特に機械学習モデルを用いて何を予測したいかを理解することが最適な評価基準を選択する上で重要となることを見てきました.
これまで数回にわたり変異原性試験データと溶解度データを用いた機械学習モデルの構築法について基本から学んできました.最近の流行はディープラーニングではありますが,これまで扱った内容をきちんと押さえることでかなりの数の論文を読みこなすことができると思います.
また一通りのことを学んできましたので,新しいデータセットについて自分でモデル構築をしてみたいという人も多いかと思います.次回はケモインフォマティクスで利用できるデータセットについて紹介してみたいと思います.
コメント