「pythonのstatsmodelsを使った重回帰分析で溶解度予測:AICによるモデル選択」という記事では,溶解度を推定する線形モデルとして以下のような記述子の一次結合を考えました.
$$ 溶解度 = \beta_{0} + \beta_{1} \times x_{1} + \beta_{2} \times x_{2} + … $$
このモデルでは「溶解度(のlog値)データはある正規分布から得られたという仮定」に基づき,各記述子における係数βを決定していきました.このような確率モデルの枠組みを「正規線形モデル」と呼びます.
一方で変異原性の有無など非連続値を,変数の線形結合を用いて予測するためには「正規分布」という仮定は不適切です.今回の記事では,二項分布やポワソン分布など正規分布以外の確率分布を仮定した場合にも適用可能な「一般化線形モデル」というものをpythonの統計モデリング用パッケージであるstatsmodelsを用いて見ていきたいと思います.
具体的には本ブログでこれまでに
- RDKitとscikit-learnで機械学習:変異原性をk-最近傍法で予測
- scikit-learnの決定木でAmes試験データセットを機械学習
- RDKitでランダムフォレスト:機械学習でも「みんなの意見」は案外正しい
などの記事で用いてきた化合物のames試験データに対して,ロジスティック回帰を用いた変異原性の有無の予測を行っていきたいと思います.
ロジスティック回帰はscikit-learnにも実装されていますが,statsmodelsを用いるとモデルの細かい統計値などが取得可能な点に違いがあります.今回の記事の最後では,scikit-learnを用いた例についても簡単に見てみたいと思います.
「Benchmark Data Set for in Silico Prediction of Ames Mutagenicity」J. Chem. Inf. Model. 2009, 49, 2077. (DOI: 10.1021/ci900161g)
一般化線形モデルとは
一般化線形モデルとは目的変数を正規分布以外の二項分布やポワソン分布などの確率分布確率分布へと拡張した線形モデルになります.例えば変異原性の有無のような現象は,コインの表裏のような事象と考えられますので,二項分布を想定することができそうです.すなわち,「ある化合物の性質(記述子)の線形結合によって変異原性が発現する確率が定まる」と考えることができます.
この時,変異原性が発現する確率pを
$$ log(\frac{p}{1 – p}) = \beta_{0} + \beta_{1} \times x_{1} + \beta_{2} \times x_{2} + … $$
の形で表現するのが一般化線形モデルによるモデル化です.
リンク関数
前項で記した式の左辺に現れている
$$ log(\frac{x}{1-x}) $$
という関数を「ロジット関数」と呼びます.この場合,変数の線形結合と目的関数を結びつけている関数(リンク関数)がロジット関数であると言います.
多変量解析のように正規分布を仮定する場合にはリンク関数は
$$ f(x) = x $$
で現される恒等関数でした.このようにどの確率分布を仮定するかに応じて,よく使われるリンク関数が決まっています.またstatsmodelsを用いてモデル化を行う際も,確率分布を選ぶことで一般的に用いられるリンク関数がデフォルトで選択されます.
上の式はpについて変形すると
$$ p = \frac{1}{1 + exp^{-(\beta_{0} + \beta_{1} \times x_{1} + \beta_{2} \times x_{2} + …)}} $$
という形になり,これをロジスティック関数と呼びます.
確率pをロジスティック関数で表現すると便利なことがあるために,逆関数であるロジット関数を用いて変数の線形結合あらわしたと言えます.
ロジスティック関数の特徴
それでは確率pをロジスティック関数で表すとどんな利点があるのでしょうか?
実はロジスティック関数は下のグラフのように,どのような大きさの入力値に対しても0から1の間のみを取ることから「確率」などを扱うのに便利な関数であると言えます.そのためニューラルネットワークなどの機械学習の分野でもよく使われています.
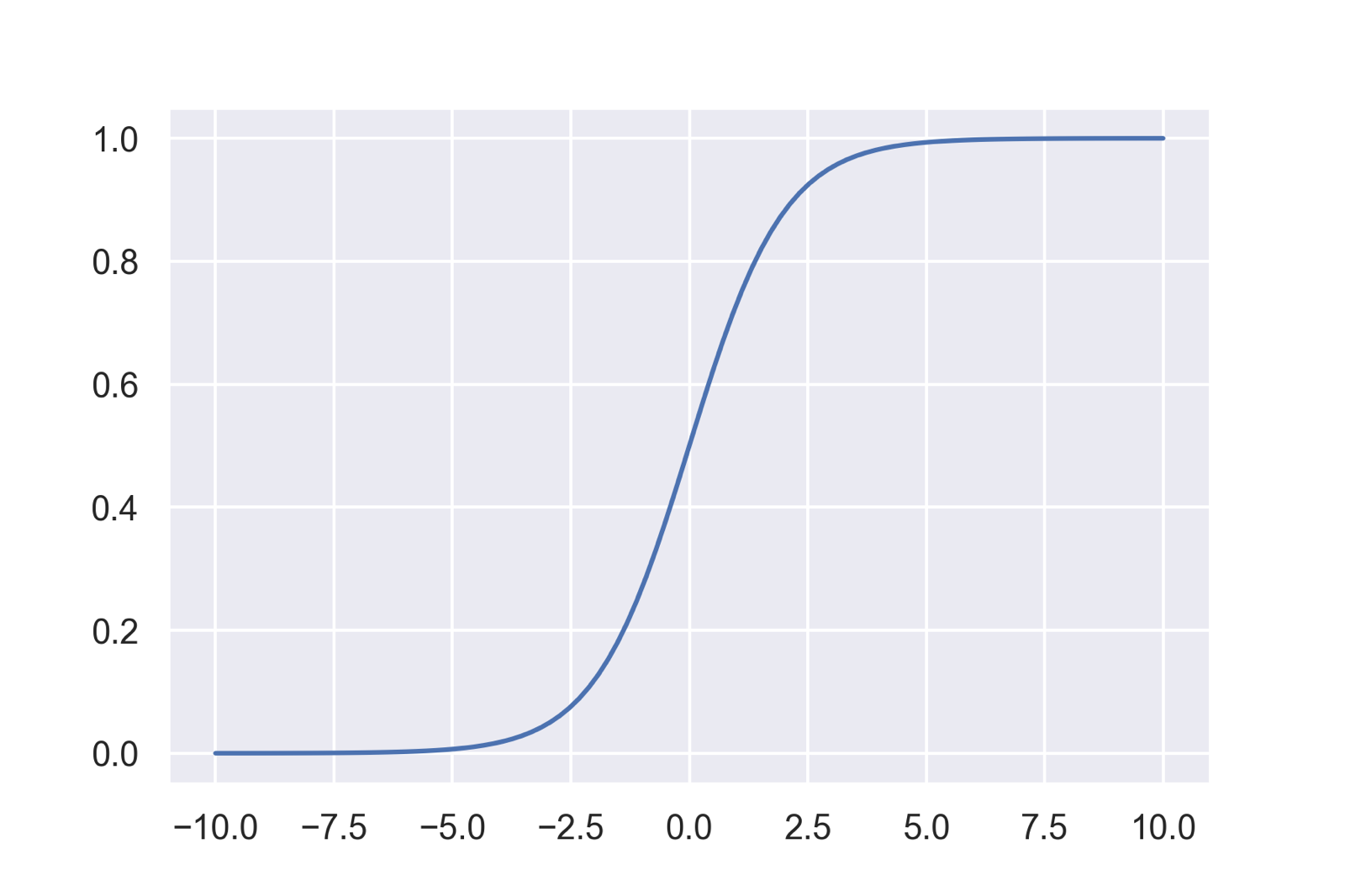
このようにロジスティック関数である事象が起こる確率pを表現し,その値の閾値以上・以下によって生起を分類するモデルを「ロジスティック回帰」と呼びます.「回帰」という名前がついていますが,「分類」を行うモデルです.
分子の準備
それでは,statsmodelsを用いてロジスティック回帰による変異原性の有無を予測するモデルを構築する前に必要なライブラリをimportし,分子を読み込んでおきましょう.
今回は3次元構造が必要な記述子も計算する予定ですので,
- SMILESが読み込めなかった分子
- 立体構造が構築できなかった分子
を2段階で削除しています.
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, PandasTools, Descriptors, Descriptors3D
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import statsmodels.formula.api as smf
import statsmodels.api as sm
print(rdBase.rdkitVersion) # 2019.03.3
df = pd.read_csv('./ci900161g_si_001/smiles_cas_N6512.smi', sep='\t', header=None)
df.columns = ['smiles', 'cas', 'result']
PandasTools.AddMoleculeColumnToFrame(smilesCol='smiles', frame=df)
# 1. 読み込めなかった分子の削除
df['mol'] = df.ROMol.map(lambda x: False if x == None else True)
df = df.drop(df[df.mol == False].index)
# 2. 立体構造が構築できなかった分子の削除
for mol in df.ROMol:
AllChem.EmbedMolecule(mol, AllChem.ETKDGv2())
failed_mols = df.ROMol.map(lambda x: x.GetNumConformers())
df = df.drop(failed_mols[failed_mols == 0].index)
len(df) # 6340
statsmodelsでロジスティック回帰モデルの構築
モデル構築に用いる記述子の選定
変異原性はいくつものメカニズムで引き起こされると考えられますが,今回のモデルでは「DNAへのインターカレーションが重要である」という仮説を立て,分子の平面性・3次元性を表す記述子をいくつか入れてモデルを構築してみたいと思います.
具体的には
- 分子量:MW
- 極性表面積:PSA
- 脂溶性:logP
- 回転可能結合数:RB
- 水素結合ドナー:HD
- 水素結合アクセプター:HA
といった6個の通常記述子に加えて,以前「RDKitで立体的な分子の形を記述する」という記事で紹介した
- Fsp3
- NPR1/NPR2
- PBF
と,「RDKitで化合物の芳香族度合を示す分子記述子を計算する」という記事で紹介した
- 芳香族指数:AP
の5つを用いてみます.
# 記述子計算
df['MW'] = df.ROMol.map(Descriptors.MolWt)
df['PSA'] = df.ROMol.map(Descriptors.TPSA)
df['Fsp3'] = df.ROMol.map(Descriptors.FractionCSP3)
df['logP'] = df.ROMol.map(Descriptors.MolLogP)
df['RB'] = df.ROMol.map(Descriptors.NumRotatableBonds)
df['AP'] = df.ROMol.map(lambda x: len(x.GetAromaticAtoms())/x.GetNumHeavyAtoms())
df['HA'] = df.ROMol.map(Descriptors.NumHAcceptors)
df['HD'] = df.ROMol.map(Descriptors.NumHDonors)
df['NPR1'] = df.ROMol.map(Descriptors3D.NPR1)
df['NPR2'] = df.ROMol.map(Descriptors3D.NPR2)
df['PBF'] = df.ROMol.map(Chem.rdMolDescriptors.CalcPBF)
# 訓練・テストセットへの分割
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
X_train, X_test, y_train, y_test = train_test_split(df[['MW', 'PSA', 'Fsp3', 'logP', 'RB', 'AP', 'HA', 'HD', 'NPR1', 'NPR2', 'PBF']],
df.result, random_state=42)
# 相関係数の可視化
fig = plt.figure(figsize=(12,10))
ax = fig.add_subplot(111)
sns.heatmap(X_train.corr().round(2), annot=True, vmax=1, vmin=-1, cmap='coolwarm')
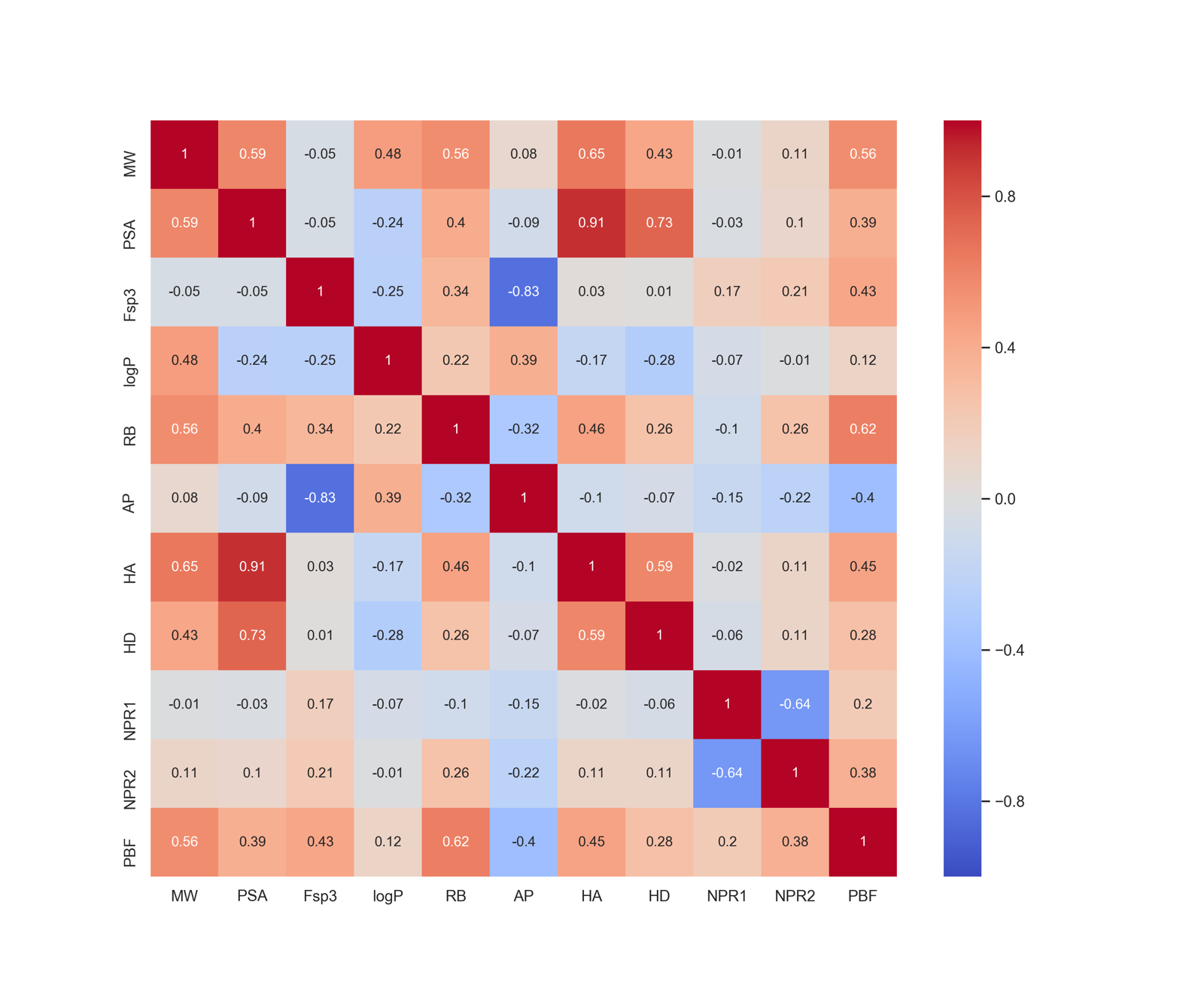
続いて分散拡大要因を計算します.
corr_inv = np.linalg.inv(np.array(X_train.corr())) vif = pd.Series(np.diag(corr_inv), index=X_train.columns) print(vif)
MW 6.416962 PSA 10.022983 Fsp3 4.196028 logP 4.653470 RB 2.511101 AP 4.296633 HA 9.013997 HD 2.850251 NPR1 4.036671 NPR2 4.149815 PBF 4.758069 dtype: float64
PSAの値が10を超えていますので,除去してモデルを構築することとします.
モデル構築とAICによるモデル選定
「pythonのstatsmodelsを使った重回帰分析で溶解度予測:AICによるモデル選択」という記事と同様に,ステップワイズ法によりモデルを構築していきましょう.
下記のコードでは10個の記述子を用いるモデルからAICが減少するように徐々に記述子の数を減らしていきます.記述子を減らしてもAICが改善しなくなった時点でモデル構築を終了します.
train_data = X_train.join(y_train)
desc_list = ['MW', 'Fsp3', 'logP', 'RB', 'AP', 'HA', 'HD', 'NPR1', 'NPR2', 'PBF']
def stepAIC(descs_l):
import copy
descriptors = descs_l
f_model = smf.glm(formula='result ~ ' + ' + '.join(descriptors),
data=train_data, family=sm.families.Binomial()).fit()
best_aic = f_model.aic
best_model = f_model
while descriptors:
desc_selected = ''
flag = 0
for desk in descriptors:
used_desks = copy.deepcopy(descriptors)
used_desks.remove(desk)
formula = 'result ~ ' + ' + '.join(used_desks)
model = smf.glm(formula=formula,
data=train_data, family=sm.families.Binomial()).fit()
if model.aic < best_aic:
best_aic = model.aic
best_model = model
desc_selected = desk
flag = 1
if flag:
descriptors.remove(desc_selected)
else:
break
return best_model
model = stepAIC(desc_list)
print(model.summary().tables[1])
AIC基準による最良のモデルは全ての記述子を用いたモデルのようです.
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -1.8055 0.547 -3.298 0.001 -2.878 -0.733
MW -0.0021 0.001 -3.065 0.002 -0.003 -0.001
Fsp3 0.4771 0.179 2.662 0.008 0.126 0.828
logP 0.1691 0.036 4.753 0.000 0.099 0.239
RB -0.0596 0.015 -3.902 0.000 -0.089 -0.030
AP 1.1053 0.193 5.719 0.000 0.727 1.484
HA 0.2986 0.027 11.267 0.000 0.247 0.351
HD -0.1418 0.033 -4.333 0.000 -0.206 -0.078
NPR1 0.8155 0.459 1.776 0.076 -0.084 1.715
NPR2 1.2947 0.541 2.394 0.017 0.235 2.355
PBF -1.6686 0.225 -7.432 0.000 -2.109 -1.229
==============================================================================
係数の正負を簡単に見てみますと,
- APの係数が正
- PBFの係数が負
とわかります.仮説通りにインターカレーションが変異原性発現に重要であるならば,芳香族指数が正の相関を示すはずでこれは感覚的によさそうです.一方でFsp3の係数も正になっているため,仮説が正しいかどうかは一概には言えなそうです.
また今回は除かれる記述子がありませんでしたが,実際に上のコードとは別に考えられる全ての組合せ1024通りについてモデルを作成して,AICをプロットした図が以下になります.モデルに組み入れる記述子の数が増えるとAICが減少していく傾向が見てとれます.
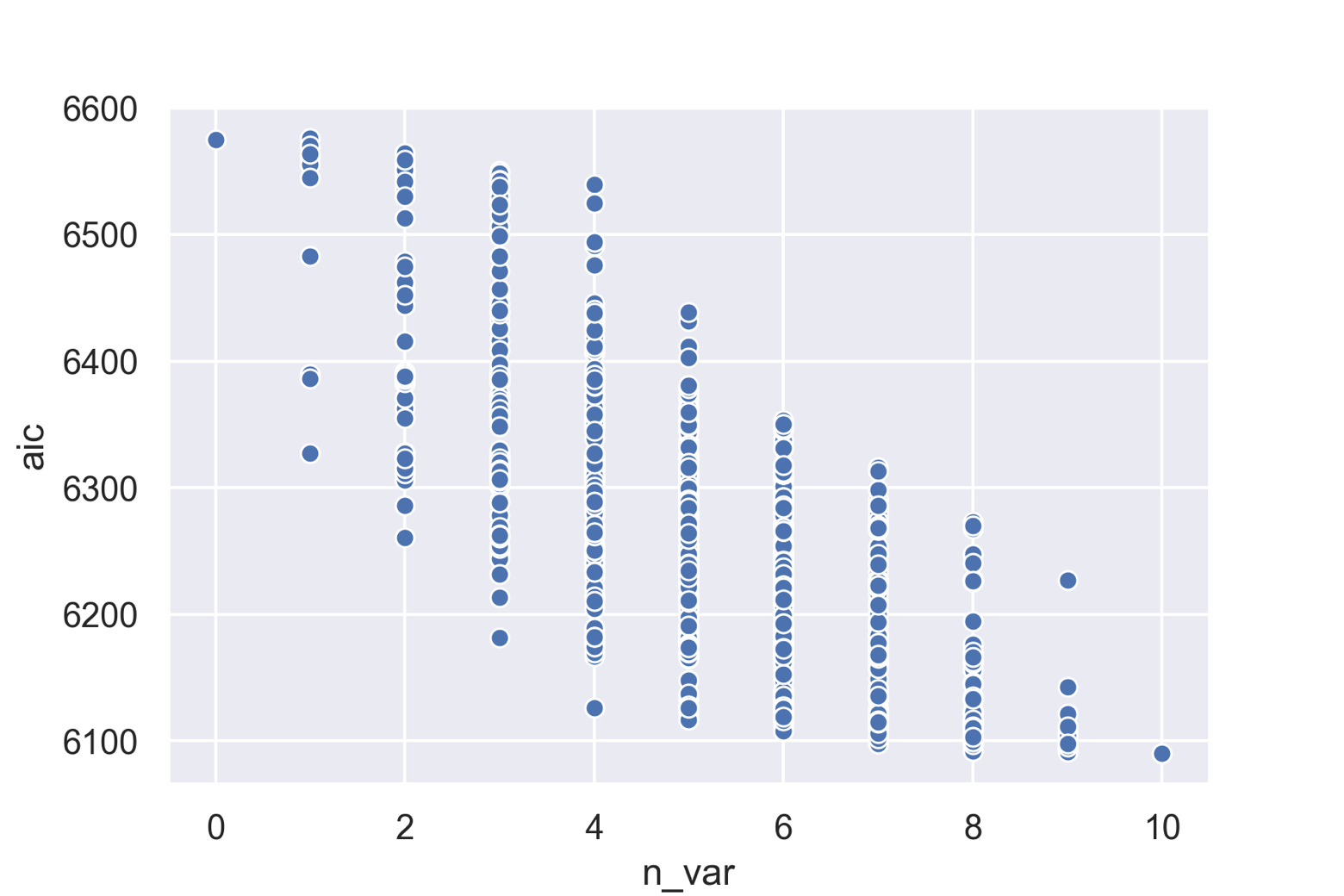
構築したモデルの評価
ロジスティック回帰の可視化
今回作成したモデルは,
$$ log(\frac{p}{1 – p}) = -1.80655-0.0021 \times MW + 0.4771 \times Fsp^{3} + … $$
という式で化合物の変異原性の確率を表現しています.この結果をグラフにしてみましょう.
eq = np.zeros(len(train_data))
for i,j in zip(model.params.index, model.params.values):
if i == 'Intercept':
eq += np.array([j])
else:
eq += j*np.array(train_data[i])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(eq, train_data.result, marker='o', alpha=0.3)
ax.plot(np.sort(eq), 1/(1+(np.exp(-np.sort(eq)))), 'k-', lw=2)
ax.set_ylabel('Result')
それっぽい図ができましたが,ちょっと精度が悪そうに見えます.
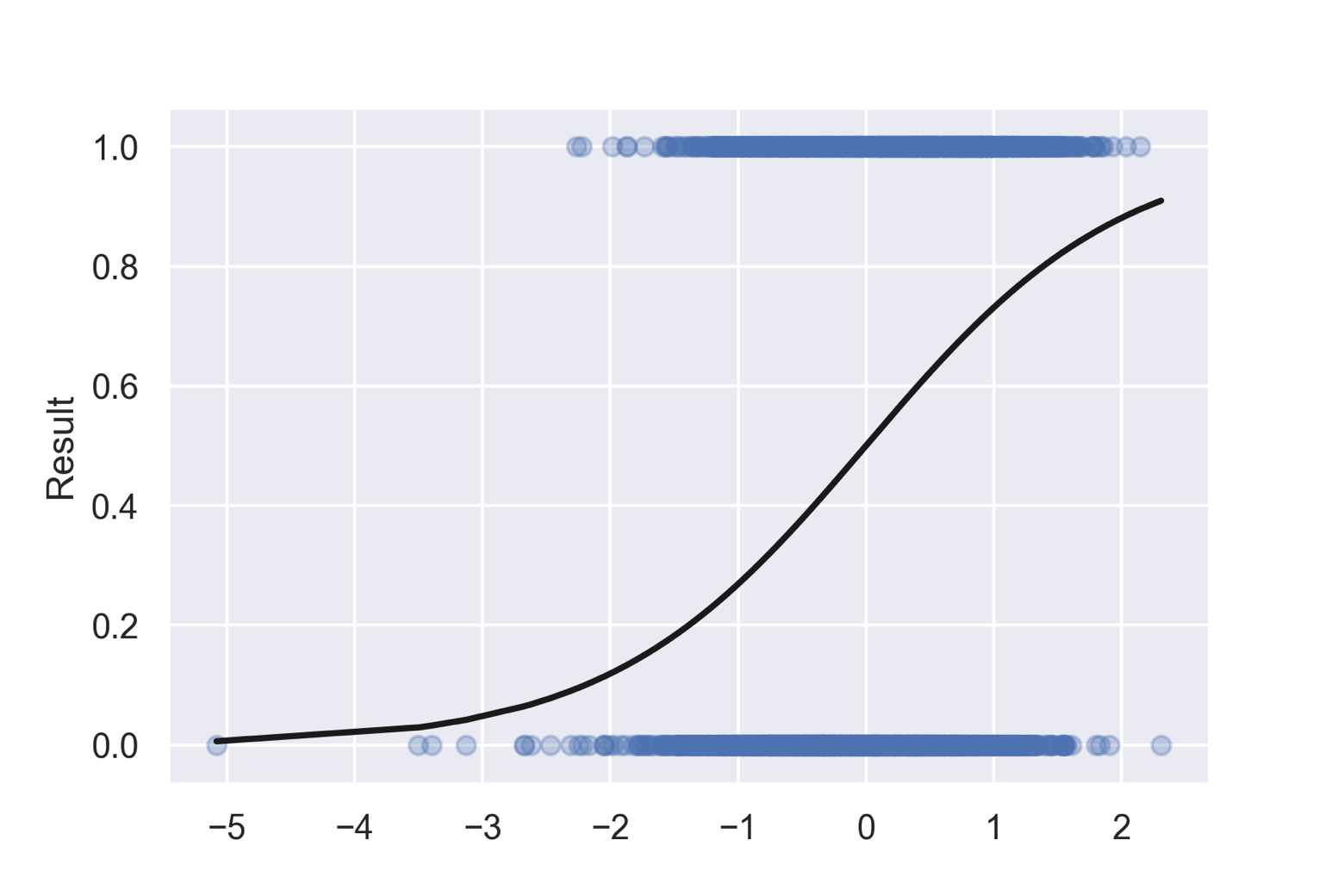
モデルの精度
続いてモデルの精度を見てみたいと思います.予測確率が0.5以上の場合を毒性あり(1)として,正解率を求めます.
ddf = pd.DataFrame({'model': model.predict()})
ddf['model_p'] = ddf.model.map(lambda x: 1 if x >= 0.5 else 0)
ddf['exp'] = np.array(train_data.result)
correct_count = len(ddf[ ddf.model_p == ddf.exp ])
print(correct_count)
print(correct_count/len(train_data))
3054 0.6422712933753943
訓練用データ全体のうち3054個が正解だったようです.正解率は0.642です.同様にしてテスト用データに対する正解率は0.621とわかりました.
「機械学習モデルの評価方法:化合物の変異原性の有無を題材に」という記事で説明した混同行列も見てみます.
from sklearn.metrics import confusion_matrix print(confusion_matrix(train_data.result, ddf.model_p))
特に偏りがあるわけではなさそうです.
[[1251 977] [ 724 1803]]
さて今回用いたデータはやや陽性の比率がやや多い(53%)データセットでした.今回構築したモデルはランダムに選んだ場合と比べて有意によいと言えるでしょうか?つまり確率0.53で表が出るコインを4755回投げた場合,3054回表が出る確率は十分に低いでしょうか?
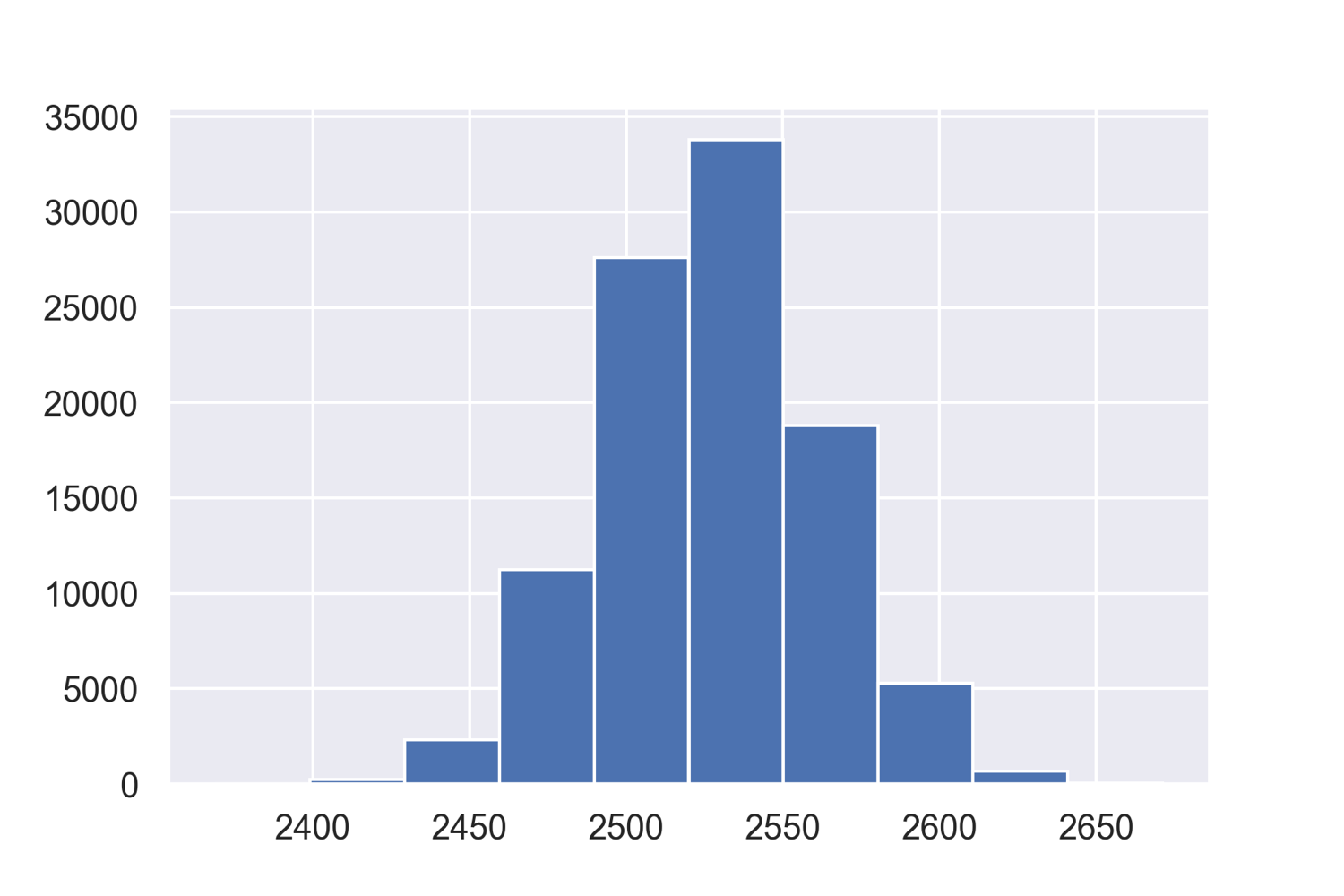
簡単に4755回のコイン投げを10万回試行してみます.
p = len(train_data.result[train_data.result == 1])/len(train_data) size = len(train_data) simulations = np.random.binomial(n=size, p=p, size=100000)
3000回も表が出ることはなさそうです.つまり今回のモデルは有効なモデルと言えそうです.
結果の解釈:係数の大きさとオッズ
ロジスティック回帰で求まる確率pは
$$ \frac{p}{1 – p} = e^{-1.80655-0.0021 \times MW + 0.4771 \times Fsp^{3} + …} $$
と書けます.左辺は今回の場合は「(毒性あり)/(毒性なし)」という比で,「オッズ」と呼ばれています.
右辺はさらに
$$ e^{-1.80655} \times e^{-0.0021 \times MW} \times e^{0.4771 \times Fsp^{3}} \times … $$
のように各記述子の効果の積で表すことが可能です.例えばlogPの係数は0.1691ですから,logPが1上がるごとにオッズがexp^(0.169)の1.18だけ上がることになります.今回のモデルによれば,logPが1増えると変異原性リスクが1.18倍になるとも表現できます.
scikit-learnとフィンガープリントを使ってロジスティック回帰
scikit-learnにもロジスティック回帰は実装されていますので,こちらとRDKitのMorganフィンガープリントを用いてモデルを構築してみます.ロジスティック回帰は「線形モデルを用いた化合物の溶解度予測:通常最小二乗法,Ridge回帰,Lasso回帰」という記事で扱ったRidge回帰やLasso回帰と同様に,sklearn.linear_modelに実装されています.モデル構築法もほぼ同様です.
from sklearn.linear_model import LogisticRegression
fps = []
for mol in df.ROMol:
fp = [x for x in AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)]
fps.append(fp)
fps = np.array(fps)
fps.shape # (6340, 2048)
targets = df.result
targets.shape # (6340,)
X2_train, X2_test, y2_train, y2_test = train_test_split(fps, targets, random_state=42)
logreg = LogisticRegression()
logreg.fit(X2_train, y2_train)
print('train score: {:.2f}'.format(logreg.score(X2_train, y2_train))
print('test score: {:.2f}'.format(logreg.score(X2_test, y2_test))
print(confusion_matrix(y2_train, logreg.predict(X2_train)))
フィンガープリントを用いると訓練用データに対する正解率に対して,テスト用データの正解率が低いので過学習が起きていることが示唆されます.
train score: 0.91 test score: 0.76 ([[2018, 210], [ 201, 2326]])
終わりに
今回は「pythonで一般化線形モデル:statsmodelsを用いたロジスティック回帰で化合物の変異原性予測」という話題について
- 一般化線形モデルの簡単な導入
- ロジスティック回帰の説明
- statsmodelsを用いたロジスティック回帰モデルの構築と評価
- scikit-learnを用いたロジスティック回帰モデルの構築
などについて説明しました.
みなさんの中には同じアルゴリズムが「統計モデル」と「機械学習」という一見異なる文脈で使われていることに疑問を感じる方がいるかもしれません.前者は現象の理解に,後者は未知データの予測に重点を置いているとも言われます.重回帰分析にしろロジスティック回帰にしろ,同じモデルをstatsmodelsとscikit-learnで構築した際に得られるモデルに関する情報がstatsmodelsの方が多いこともこれを反映していると考えられます.
いずれにせよ,モデルの背後にある数学は同じですので,本ブログでは対象とする問題に応じてどちらも使っていきたいと思います.次回も線形モデルについてもう少し見ていく予定です.
コメント