RDKitとk平均法による化合物の非階層型クラスタリング

「RDKitでフィンガープリントを使った分子類似性の判定」という記事では分子のフィンガープリントを導入することで分子の類似度を評価しました．類似度が高い分子の組み合わせは，化合物空間（ケミカルスペース）における距離が近いと言い換えることができます．この場合，「類似度」と「距離」は反対の意味に使われます．距離が遠い化合物を選ぶことで，多様なライブラリーが構築できることになります．

多様性の高いライブラリーを構築するためには

クラスタリング法
距離ベースの方法
区分けをベースとした方法
最適化手法を用いる方法

といった４つの手法が代表的です．

今回は非階層型クラスタリング手法の１つであるk平均法を用いて，化合物ライブラリーから「多様な」化合物を選択していきたいと思います．

なお多様なライブラリーの構築法については「ケモインフォマティクスで多様なライブラリーを構築する」という記事に全体像をまとめていて，本記事は各論になります．

ケモインフォマティクスで多様な化合物ライブラリーを構築する

本サイトでは「有機合成化学者のためのケモインフォマティクス入門」を掲げて，高価なソフトウェアを用意することなく学習がはじめられるようにプログラミング言語pythonとそのケモインフォマティクス用ライブラリーであるRDKitを用いた解説をおこなっています．「RDKitでフィンガー...

分子とライブラリの準備
フィンガープリントと距離行列の計算
k平均法によるクラスタリング
分類したクラスターから分子を選択
主成分分析によるケミカルスペースの可視化
終わりに

分子とライブラリの準備

今回はナミキ商事の運営するChemCupidからダウンロードした，カタログの新規追加分の分子を収めたSDFを使いたいと思います．

塩の化合物は扱いにくいので，NScodeが0000で終わるもの（フリー体）のみを読み込んでいます．全部で66005個の分子になりました．

最後に分子の順番をランダムにシャッフルします．クラスタリングには最初の5000個を用いることにします．

### ライブラリのimport
from rdkit import rdBase, Chem, DataStructs
from rdkit.Chem import AllChem, Draw
from rdkit.Chem.Draw import rdMolDraw2D
import numpy as np
%matplotlib inline
print(rdBase.rdkitVersion) ### 2017.03.3
### 分子の準備
suppl = Chem.SDMolSupplier('./Namiki_NEW_201807_0001.sdf')
mols_free = [x for x in suppl if x is not None if x.GetProp('NScode').endswith('0000')]
len(mols_free) ### 66005
### シャッフル
np.random.seed(1234)
np.random.shuffle(mols_free)

numpyを用いた乱数に発生については「NumPyのrandomルーチンでいろいろな乱数を生成する」という記事で解説しています．参照してみてください．

フィンガープリントと距離行列の計算

AllChem.GetMorganFingerprintAsBitVect(mol, radius, nBits)
DataStructs.BulkTanimotoSimilarity(refFP, FP_list)

読み込んだ全ての分子に対して2048ビット長Morganフィンガープリントを生成した後に，クラスタリングに用いる距離行列を作成します．BulkTanimotoSimilarityはデフォルト設定ではタニモト係数のリストを返しますが，returnDistance=Trueオプションを設定すると「1 – タニモト係数」で距離を計算して返します．

距離行列は対称ですので，上または下三角部分だけを計算すればよいのですが，今回は全部計算しています．

最後にあとでscikit-learnで扱うために行列をnumpy.ndarrayに変換しています．

### 距離行列の計算
morgan_fp = [AllChem.GetMorganFingerprintAsBitVect(x,2,2048) for x in mols_free]
dis_matrix = [DataStructs.BulkTanimotoSimilarity(morgan_fp[i], morgan_fp[:5000],returnDistance=True) for i in range(5000)]
### numpy.ndarrayへの変換
dis_array = np.array(dis_matrix)
dis_array.shape ### (5000, 5000)

k平均法によるクラスタリング

sklearn.cluster.KMeans(n_clusters)

k平均法はpythonの機械学習用ライブラリscikit-learnに実装されています．今回は6個のクラスタに分けることにしました（n_clusters=6）．

学習した結果のクラス分けはlabels_に格納されていますので，クラスタリングごとに集計をしてみましょう．

from sklearn.cluster import KMeans
import pandas as pd
kmeans = KMeans(n_clusters=6)
kmeans.fit(dis_array)
kmeans.labels_[:20]
pd.value_counts(kmeans.labels_)

極端に少ないグループはなさそうです．

クラス	個数
2	979
0	953
1	933
5	884
4	633
3	618

分類したクラスターから分子を選択

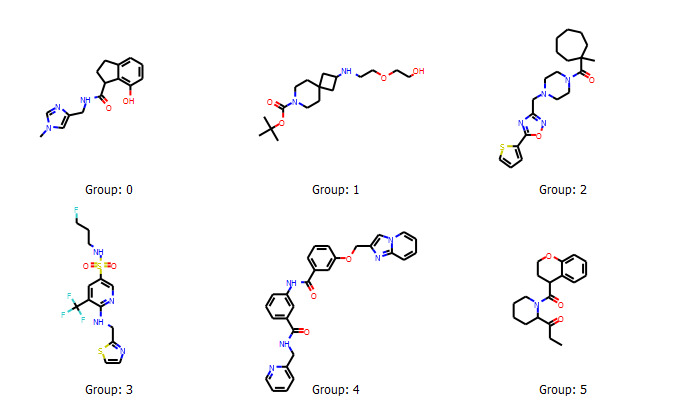
個々のクラスターから分子を選ぶ方法は色々と考えられますが，今回はlabels_ごとに辞書型にして化合物をクラスターごとにまとめてから，ランダムに1つの分子を選択しました．

kmeans_library = {i: [] for i in range(6)}
for n,j in enumerate(kmeans.labels_):
    kmeans_library[j].append(mols_free[n])
selected_compounds = [np.random.choice(kmeans_library[i]) for i in range(6)]

選ばれた分子は以下のようなものたちでした．多様性があると言えるでしょうか？

主成分分析によるケミカルスペースの可視化

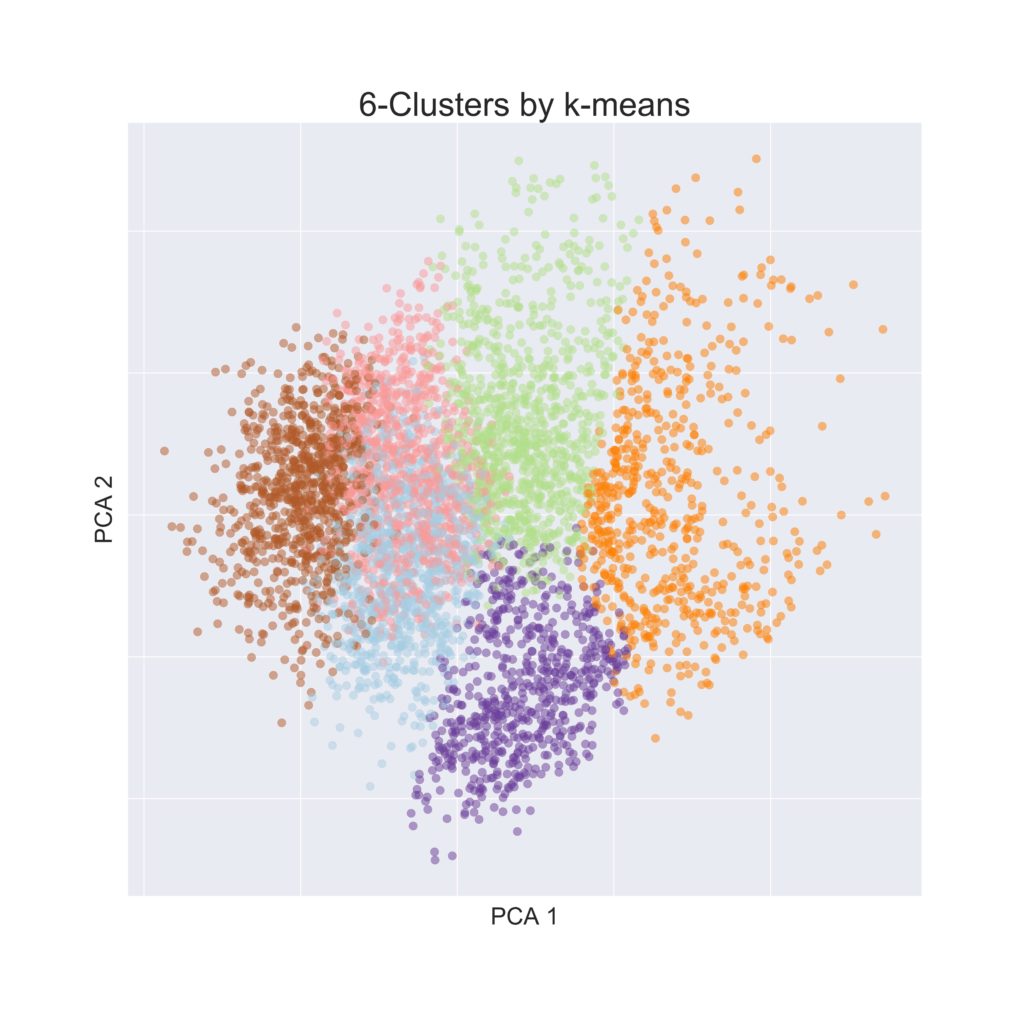
sklearn.decomposition.PCA(n_components)

今回用いた距離行列は5000 x 5000でした．つまり1つの分子が5000個の特徴量で表されていることになります．5000次元の空間を可視化することはできませんので，どうにかして我々が扱える次元（２または３次元）にまで落とし込む必要があります．こういった次元削減によく使われるのが「主成分分析（PCA）」という方法です．

scikit-learnではsklearn.decompositionに実装されています．今回はPCAを用いて距離行列を2次元に落とし込んで可視化することで，さきほどのk平均法によるクラスタリングがどのように行われているかを可視化してみます．

### モデル構築と変換
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(dis_array)
dis_pca = pca.transform(dis_array)
### 可視化
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
ax.scatter(dis_pca[:,0], dis_pca[:,1], s=50, c=kmeans.labels_, cmap='Paired', alpha=0.5)
ax.set_xlabel('PCA 1', fontsize=20)
ax.set_xticklabels([])
ax.set_ylabel('PCA 2', fontsize=20)
ax.set_yticklabels([])
ax.set_title('6-Clusters by k-means', fontsize=28)

うまい具合にクラスタリングできているようです．