これまで本ブログではpythonを用いて計算化学を学習するために,「計算化学にPythonとPsi4で入門」という記事から始め,いくつかの記事で量子化学計算用ライブラリPsi4の使い方を紹介してきました.
これまでの計算は全て真空中での孤立分子を対象に行ってきました.このような限定的な条件においても量子化学計算は分子の構造やエネルギーに関し有用な示唆を与えてくれますが,溶液中の分子のモデルとしては必ずしも適切とは言えません.
今回の記事では
- 計算化学における溶媒効果の扱い方
- 分極連続体モデルを扱うPCM Solverとは何か
- Psi4におけるPCM Solverの使い方
などについて説明していくことで,計算化学における溶媒効果の扱い方に関し理解を深めていきます.

連続誘電体モデルとは
溶媒効果は
- 溶媒の分極や双極子配向などの長距離効果
- 水素結合やファン・デル・ワールス相互作用などの近距離効果
の2つに分けることができます.前者の効果は主に,溶質分子による溶媒の分極と電気多極子の配向であり,ある誘電率を有する均一の媒体(連続誘電体)として溶媒を考えることでモデル化できます.
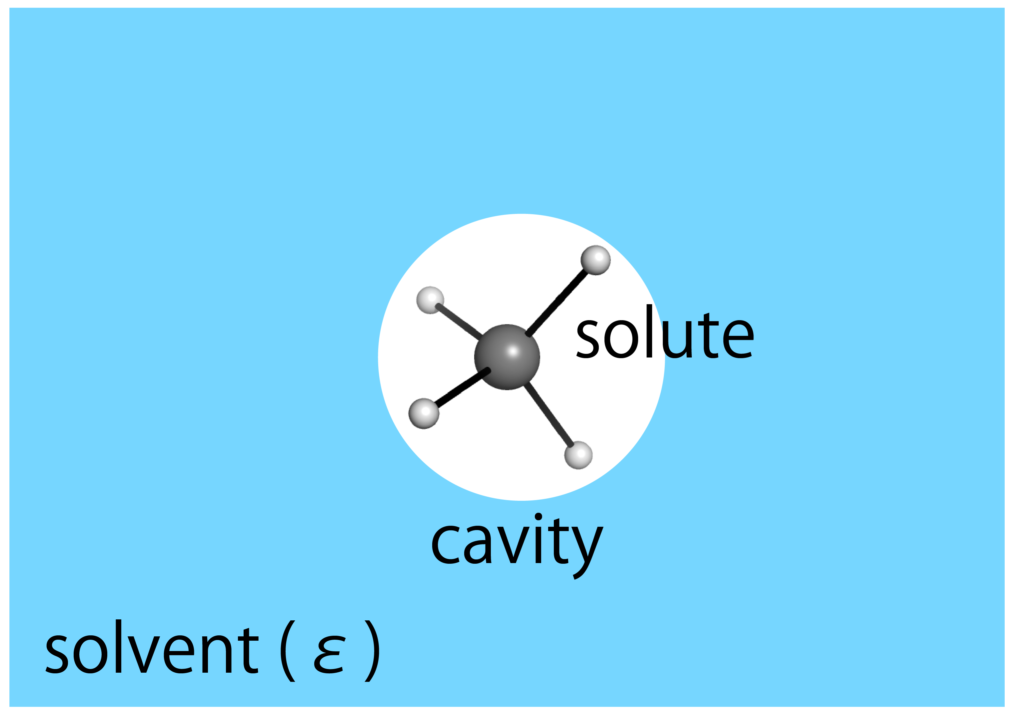
連続誘電体による溶媒効果のモデル化
溶媒効果とは溶媒中に適切な空孔を置くことで得られるエネルギーです.空孔を作成すること自体は不安定効果を持ちますが,溶質と溶媒の分散力や静電相互作用等の安定化効果があるためにトータルでは安定化効果があると見込まれます.溶媒効果を定式化すると以下のようになるでしょう.
$$ \Delta G_{solvation} = \Delta G_{cavity} + \Delta G_{elec} + \Delta G_{dispersion} + \Delta G_{exchange} + \Delta G_{H-Bond} + … $$
連続誘電体としては誘電率εのみを考えますが,これは静電相互作用を定義付けるに過ぎません.例えばアセトン(ε=20.7)と1-プロパノール(ε=20.1)は似たような誘電率を持ちますが,水素結合能など溶媒としての特徴はかなり異なります.これら性質の違いは非静電相互作用項のパラメータ化によって反映されています.
空孔の形
空孔の形は溶媒効果の計算に重要な影響を及ぼします.研究初期では計算の容易な球状の空孔が使われていましたが,多くの分子は球状からはほど遠い形をしています.そのため,
- 電子密度
- SAS
- ファン・デル・ワールス表面
の利用が提案されてきました.多くの場合は算出の容易さから原子半径に一定値(1.2が典型)を掛けたファン・デル・ワールス表面を採用することが多いです.
自己無撞着反応場
連続誘電体モデルでは溶質分子は溶媒中の空孔(cavity)の中に置きます.溶質の電荷分布が溶媒を分極することで反応場が生じ,生じた場が今度は溶質分子に影響を与えます.このような相互作用が自己矛盾ないように求める枠組みをSCRF(Self-Consistent Reaction Field),自己無撞着反応場と言います.
また分極する連続誘導体を考えるため,PCM(Polarizable Continuum Model)と呼ばれます.パラメータ化の違いによって様々なPCMモデルが提唱されていますが,IEFPCM(Integral Equation Formalism PCM)が最もポピュラーです.
PCM Solver
PCM Solverはpsi4のような外部プログラムと連携することで,PCMモデルによって溶媒効果を取り入れられるように設計されています.計算に必要な情報を入力したインプットファイルは下記に示すように一定のルールに従って用意する必要があります.基本的にリーズナブルなデフォルト値が設定されているため,利用者側で指定する必要があるものはごく一部です.
Units
インプットファイルで扱う単位を指定します.通常はangstromを用います.
Cavityセクション
溶質を内包するcavityに関する設定を記述します.前述の通りどのような空孔,cavityを作成するかが溶媒モデルの肝になります.
| オプション名 | 説明 | デフォルト値 |
|---|---|---|
| Type | どのように表面を作成するか.通常はGEPOL(GEnerating POLyhedra)アルゴリズム. | — |
| Scaling | 原子半径を1.2倍に拡大して使うか否か | True |
| RadiiSet | Bondi, UFF, Allingerのうちどの原子半径セットを使うか | Bondi |
| Mode | 分子表面をどのように作成するか.psi4のような外部プログラムと連携する場合はimplicitを選びます. | Implicit |
Mediumセクション
SolverTypeオプションでは
- IEFPCM(Integral Equation Formalism)
- CPCM(Conductor-like)
の2つのPCMモデルが選択可能です.
またSolventオプションでは以下の溶媒が選択可能です.
| solvent name | 分子式 |
|---|---|
| Water | H2O |
| Propylene Carbonate | C4H6O3 |
| Dimethylsulfoxide | DMSO |
| Nitromethane | CH3NO2 |
| Acetonitrile | CH3CN |
| Methanol | CH3OH |
| Ethanol | CH3CH2OH |
| Acetone | C2H6CO |
| 1,2-Dichloroethane | C2H4CL2 |
| Methylenechloride | CH2CL2 |
| Tetrahydrofurane | THF |
| Aniline | C6H5NH2 |
| Chlorobenzene | C6H5CL |
| Chloroform | CHCL3 |
| Toluene | C6H5CH3 |
| 1,4-Dioxane | C4H8O2 |
| Benzene | C6H6 |
| Carbon Tetrachloride | CCL4 |
| Cyclohexane | C6H12 |
| N-heptane | C7H16 |
Psi4でPCM Solverを使う
psi4.pcm_helper(pcm-input)
psi4でPCM Solverを利用するにはpcmオプションをTrueにし,pcm_helperを用いて上記のフォーマットに従って作成したPCM Solverのインプットファイルを読み込みます.具体的な形は次項で見ていきましょう.
1,2-ジフルオロエタンの溶媒効果
これまでも本ブログでは「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」や「psi4における振動数計算:IRスペクトルや異性体間のエネルギー差を計算」といった記事で,1,2-ジフルオロエタンのanti体とgauche体のエネルギー差を題材としてきました.
anti体は双極子モーメントが0であるのに対し,gauche体は双極子モーメントがあります.安定配座であるgauche体の方が極性溶媒中ではさらに安定化されるため,二つの配座間のエネルギー差が拡大すると予想できます.今回はこの点を確認していきます.
下記のコードでは,
- anti体とgauche体をそれぞれwB97X-D/6-31+G(d,p)レベルで構造最適化と振動数計算
- それぞれの最適化構造に対して,真空中でwB97X-D/6-311+G(d,p)レベルのエネルギーと双極子モーメントを計算
- 真空中でのエネルギー差を出力
- それぞれの(真空中での)最適化構造に対して,水中でwB97X-D/6-311+G(d,p)レベルでのエネルギーと双極子モーメントを計算
- 水中でのエネルギー差を出力
という手順で計算しています.
PCM Solverのインプットは以下のように
- IEFPCM
- Water
- UFF半径
- 1.2倍にスケーリング
という内容を,pythonicな形式ではありませんがpythonのstringオブジェクトとして入力します.
# PCM Solverのインプット
pcm = '''
units = angstrom
medium
{
solvertype = iefpcm
solvent = Water
}
cavity
{
type = gepol
scaling = True
radiiset = uff
mode = implicit
}
'''
import sys
import pathlib
import numpy as np
import psi4
print(f'python version:\n{sys.version}')
# python version:
# 3.9.7 (default, Sep 16 2021, 13:09:58)
# [GCC 7.5.0]
print(f'numpy version:\t{np.__version__}')
# numpy version: 1.21.2
print(f'psi4 version:\t{psi4.__version__}')
# psi4 version: 1.5
filename = pathlib.Path(__file__)
logfile = filename.with_suffix('.log').name
psi4.set_output_file(logfile)
psi4.set_memory('14GB')
psi4.set_num_threads(12)
# 初期構造の定義
gauche = psi4.geometry('''
0 1
C -1.19543643 -0.19841270 0.00000000
H -0.83878201 -1.20722270 0.00000000
H -0.83876359 0.30598549 -0.87365150
C -0.68209421 0.52754358 1.25740497
H -1.04036332 0.02427515 2.13105486
H 0.38790398 0.52583689 1.25838372
F -2.54543643 -0.19839606 0.00000000
F -1.13006250 1.80105168 1.25617165
''')
anti = psi4.geometry('''
0 1
C -1.19543643 -0.19841270 0.00000000
H -0.83878201 -1.20722270 0.00000000
H -0.83876359 0.30598549 -0.87365150
C -0.68209421 0.52754358 1.25740497
H -1.03874884 1.53635351 1.25740509
H -1.03876691 0.02314493 2.13105626
F -2.54543643 -0.19839606 0.00000000
F 0.66790579 0.52752676 1.25740465
''')
au2kcal = psi4.constants.hartree2kcalmol
level = 'wb97x-d/6-31+G(d,p)'
# PCM Solverのインプット
pcm = '''
units = angstrom
medium
{
solvertype = iefpcm
solvent = Water
}
cavity
{
type = gepol
scaling = True
radiiset = uff
mode = implicit
}
'''
# 構造最適化+振動数計算を実施する関数
def optfreq(mol: psi4.core.Molecule) -> tuple[float, psi4.core.Wavefunction]:
_, wfn = psi4.optimize(level,
molecule=mol,
return_wfn=True)
energy, wfn = psi4.frequency(level,
molecule=mol,
ref_gradient=wfn.gradient(),
return_wfn=True)
return (energy, wfn)
# 双極子モーメントを計算する関数
def get_dipole(wavefunction: psi4.core.Wavefunction) -> float:
psi4.oeprop(wavefunction, 'dipole')
dipole = psi4.variable('scf dipole')
dipole = np.sqrt(np.sum(dipole ** 2))
return dipole
psi4.set_options({'geom_maxiter': 200})
# 構造最適化+振動数計算
print(f'optimizing anti conformer in the gas phase.....')
anti_energy_gas, anti_wfn_gas = optfreq(anti)
print(f'optimizing gauche conformer in the gas phase.....')
gauche_energy_gas, gauche_wfn_gas = optfreq(gauche)
# 真空中でのエネルギー計算
sp_level = 'wb97x-d/6-311+G(d,p)'
print(f'calculating single point energy of anti conformer in the gas phase.....')
anti_energy_gas, anti_wfn_gas = psi4.energy(sp_level,
molecule=anti,
return_wfn=True)
anti_dipole_gas = get_dipole(anti_wfn_gas)
print(f'anti dipole moment in the gas phase:\t{anti_dipole_gas:.3f}\n')
print(f'calculating single point energy of gauche conformer in the gas phase.....')
gauche_energy_gas, gauche_wfn_gas = psi4.energy(sp_level,
molecule=gauche,
return_wfn=True)
gauche_dipole_gas = get_dipole(gauche_wfn_gas)
print(f'gauche dipole moment in the gas phase:\t{gauche_dipole_gas:.3f}\n')
energy_diff_gas = au2kcal * (anti_energy_gas - gauche_energy_gas)
print(f'energy difference in the gas phase (anti - gauche):\n{energy_diff_gas:.2f}')
# PCMの設定
print('\n#\t#\t#\t#\t#\t#\n')
psi4.set_options({'pcm': True})
psi4.pcm_helper(pcm)
# 溶媒中でのエネルギー計算
print(f'calculating single point energy of anti conformer in the aq phase.....')
anti_energy_aq, anti_wfn_aq = psi4.energy(sp_level,
molecule=anti,
return_wfn=True)
anti_dipole_aq = get_dipole(anti_wfn_aq)
print(f'anti dipole moment in the aq phase:\t{anti_dipole_aq:.3f}\n')
print(f'calculating single point energy of gauche conformer in the aq phase.....')
gauche_energy_aq, gauche_wfn_aq = psi4.energy(sp_level,
molecule=gauche,
return_wfn=True)
gauche_dipole_aq = get_dipole(gauche_wfn_aq)
print(f'gauche dipole moment in the aq phase:\t{gauche_dipole_aq:.3f}\n')
energy_diff_aq = au2kcal * (anti_energy_aq - gauche_energy_aq)
print(f'energy difference in the aq phase (anti - gauche):\n{energy_diff_aq:.2f}')
出力結果は以下のようになりました.anti体からgauche体のエネルギーを引いた値を出力していますので,数字が大きいほどgauche体の方が安定となります.予想通りに水中ではgauche体がより安定化されることが示されました.
| 条件 | エネルギー差(kcal/mol) |
|---|---|
| 真空中 | 0.81 |
| 水中 | 2.07 |
終わりに
今回は「Psi4で溶媒効果を考慮する:PCM Solverの使い方」という話題について,
- 計算化学における溶媒効果の取り扱い方
- 分極連続体モデルとPCM Solverについて
- Psi4を通じてPCM Solverの使い方
- 1,2-ジフルオロエタンを例とした具体的な計算の仕方
などを説明してきました.
PCMモデルでは溶媒の分極などに起因する長距離の溶媒効果しか考慮することができません.一方で我々が興味のある系では,溶媒と溶質が水素結合などを通じて直接相互作用し溶質の構造を大きく変化させる場合もあります.次回はそのような場合もモデル化が可能な溶媒分子をあらわに扱う方法について触れたいと思います.
>>次の記事:「Psi4で溶媒の直接関与を考慮する」
コメント
いつも詳しい解説ありがとうございます。私もpsi4やインフォマティクスに関心があり、少しづつですが、触り始めています。いつも勉強させて頂いているので、お礼を言いたくてコメントさせていただきました。
winchem様
ご丁寧にコメントありがとうございます.今後とも当ブログをよろしくお願い申し上げます.
計算化学のことを勉強したいと思い、探しているうちに本サイトを発見し拝見しております。大変参考になる記事をたくさんありがとうございます。書籍を購入して本サイトの記事と合わせて少しづつ勉強しております。
「PCM Solverはpsi4のような外部プログラムと連携することで、、、」と記載がありますが、PCMを利用するために別途何かをインストールする必要がありますでしょうか?
Psi4 ver.1.8.1でwidows版でもPCM solverが利用可能になった(Conda PackageにPCM solverが含まれる)とPsi4のリリースノートに記載があるので1.8.1以降であればPCMのインプットコマンドを入力すれば利用可能なのでしょうか。
(私はwindows11, Psi4 ver.1.9.1_conda3.11を利用しています)。
本サイトでお聞きするのは場違いかもしれませんが、ご教授いただけると助かります。
お忙しいところ恐縮ですがよろしくお願いいたします。
りん様
拙著をご購入頂いたとのこと,ありがとうございます。
ご質問の件ですが,Psi4 1.9のRelease Noteにある「includes PCMSolver (backported to v1.8.1)」は
condaでPsi4をインストールした際にPCMSolverも一緒にインストールされるようになったというご理解で正しいです。
そのため別途何かをインストールする必要はございません。
ご自身の環境で「conda list」をタイプしてインストールされたライブラリーを調べてみると,
PCMSolverが一緒に入っていることが確認できると思います。
今後ともよろしくお願いいたします。
返信が遅くなり申し訳ございません。
ご回答いただきありがとうございました。