分子間の結合の生成やリガンドの受容体への結合を始めとする興味深い化学現象は分子同士の相互作用を駆動力として生じます.そのため分子間相互作用を理解することは重要であり,計算化学を用いることでその理解を深めることができます.
今回は2つの分子の会合体形成を例として,計算化学を用いてどのように「相互作用エネルギー」を考えていくかをみていきます.その中で「超分子法」や「基底関数重なり誤差」といった重要な概念を学んでいきます.

超分子法を用いた分子間相互作用エネルギーの計算
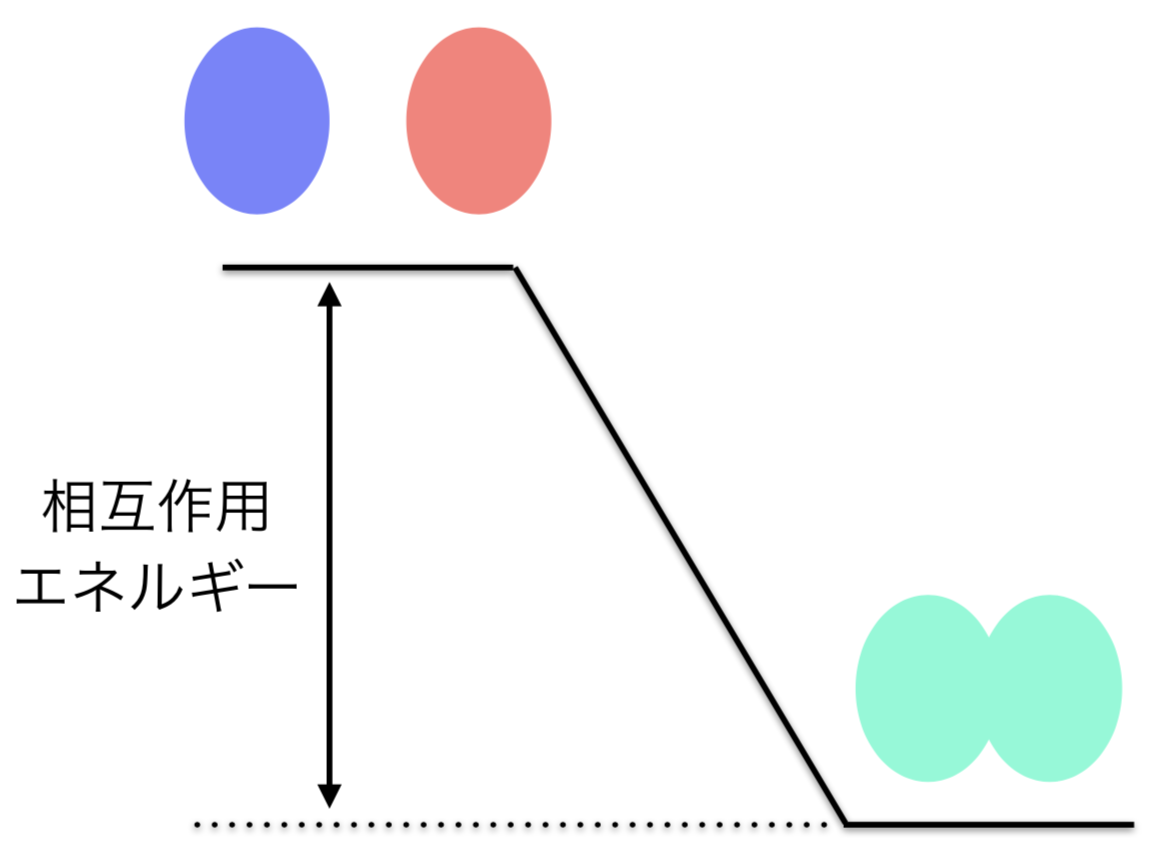
分子間相互作用エネルギーを求めるには「超分子法」という方法が用いられます.超分子法の英語表記は超分子化学の「supramolecule」ではなく「supermolecule」です.
超分子法では
- 2つの分子からなる会合体のエネルギー(下図の緑)
- その構成成分であるモノマーのエネルギーの和(下図の青と赤)
の差を取ることで相互作用エネルギーを計算します.すなわち相互作用エネルギーは下記の式で表せます.
$$ E_{int} = E_{A+B}\ -\ E_A\ -\ E_B $$
基底関数重なり誤差とは
超分子法のように異なる計算で得たエネルギーを比較するには,用いる計算レベルを揃える必要があります.会合体のエネルギー計算における問題点として,「会合体とモノマーの計算で変分自由度が異なる」ことが挙げられます.
これは会合体中のA(青)に相当する部分を計算する際に,B(赤)上にある基底関数も使ってしまうことに起因し,このために相互作用エネルギーが過大評価されてしまいます.これを「基底関数重なり誤差(BSSE: Basis Set Superposition Error)」と言います.
BSSEは基底関数の数や広がりが不十分であることが原因ですので,より大きな基底関数系を用いることでBSSEを減らすことができます.しかし現実的に用いられる6-311+G(d,p)などのトリプルゼータ基底関数系ではBSSEが無視できるレベルにはならないことから,他の方法でBSSEを取り除く方法が考案されています.
Counterpoise法(CP法)
BSSEを除く方法として最も使われているのがCounterpoise法(CP法)と呼ばれる方法です.CP法ではモノマーAの計算を行う際にもBの基底関数を利用できるようにして計算を行います.この際にはBに該当する原子位置には「ゴーストアトム」と呼ばれる原子核も電子も持たない原子を置くことで,Aのエネルギー計算にB由来の基底関数だけを取り込みます.
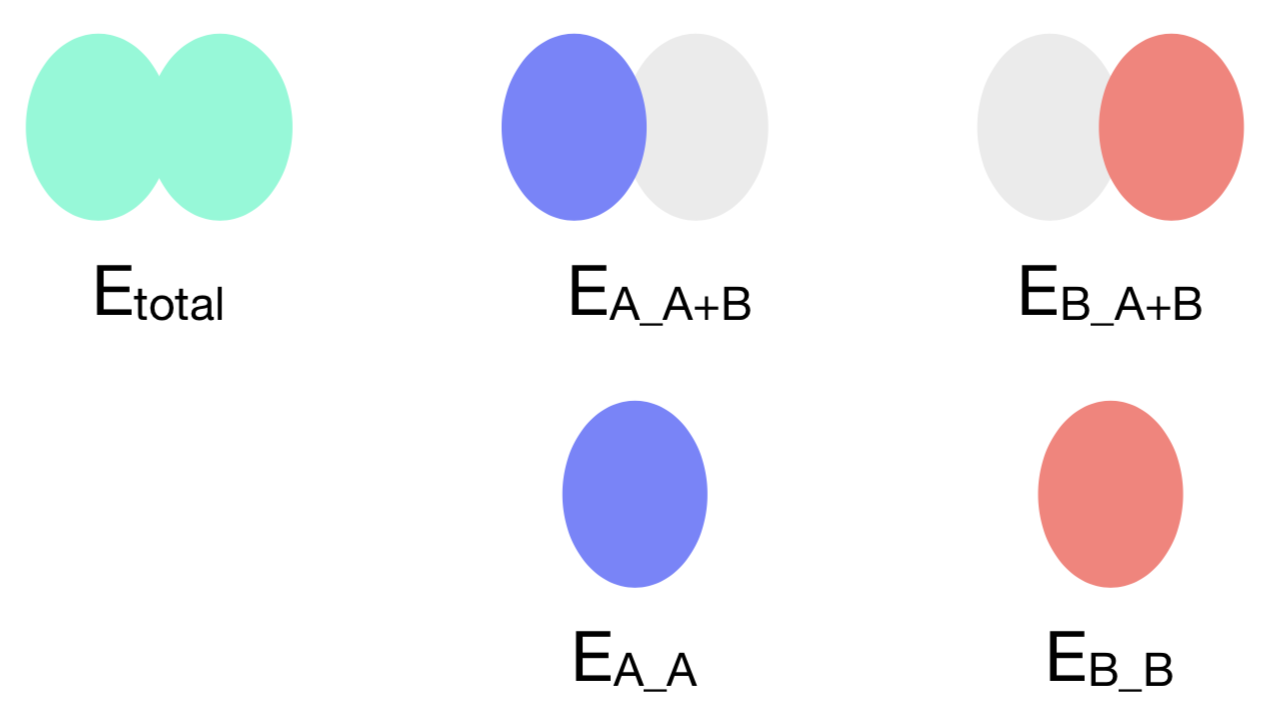
下の図で
- EA;A+B:A+Bの基底関数を使って計算したAのエネルギー
- EB;A+B:A+Bの基底関数を使って計算したBのエネルギー
を表しているとすると,CP法で補正した相互作用エネルギーは
$$ 相互作用エネルギー = E_{total} – (E_{A;A+B} + E_{B;A+B}) $$
と書けます.またBSSEは
$$ BSSE = (E_{A;A} + E_{B;B}) – (E_{A;A+B} + E_{B;A+B}) $$
となります.
Psi4を用いたBSSEの補正
それではpsi4を用いて相互作用エネルギーの計算を行っていきます.今回は三フッ化ホウ素(BF3)とアンモニア(NH3)の相互作用を考えていきます.有機化学でよく見られる典型的なルイス酸とルイス塩基の相互作用です.
CP法
CP法による補正はよく使われる方法ですので,Psi4ではエネルギー計算においてbsse_type=’cp’とすることで簡単に利用可能です.戻り値がそのまま補正済み相互作用エネルギー(a.u.)になります.
計算にあたってAとBの部分構造を指定するために入力座標設定のXYZブロックの中で「- -」を用いてフラグメントを分ける必要があります.
下のコードでは
- MP2/6-31G(d)で会合体の構造最適化
- CP法を用いて同レベルでエネルギー計算
という手順で行っています.
import psi4
import time
now = time.strftime('%Y%m%d-%H%M')
## CPUとメモリの設定は各自の環境にあわせてください
psi4.set_num_threads(10)
psi4.set_memory('14GB')
psi4.set_output_file(now + '_BSSE_Ghost.log')
au2kcal = psi4.constants.hartree2kcalmol
## --を使ってBF3とNH3のフラグメントを指定
bf3nh3 = '''
0 1
B -0.23097800 0.00000200 -0.00000200
F -0.54584700 -1.30452400 -0.27264200
F -0.54577900 0.88838500 -0.99344800
F -0.54583800 0.41616900 1.26606400
--
0 1
N 1.48202700 -0.00002600 0.00002300
H 1.83930300 0.93578300 0.19428800
H 1.83927700 -0.63617400 0.71333300
H 1.83929600 -0.29970200 -0.90754200
'''
## 1. 構造最適化
mol = psi4.geometry(bf3nh3)
e_total = psi4.optimize('mp2/6-31G(d)', molecule=mol)
optimized_coord = mol.save_string_xyz()
## 2. CP法によるエネルギー計算
e_cpcorr = psi4.energy('mp2/6-31G(d)', bsse_type='cp', molecule=mol)
print('CP corrected interaction energy: {:.2f}'.format(au2kcal * e_cpcorr))
相互作用エネルギーは40.1 kcal/molでした.
CP corrected interaction energy: -40.10
ゴーストアトムを用いたエネルギー計算
続いてゴーストアトムを用いてエネルギー計算を行ってみます.psi4ではXYZ形式の「元素記号の前に@を付ける」ことでゴーストアトムの設定ができます.
下記コードでは,先ほどの最適化した構造のXYZブロックを用いて
- BF3のみ
- BF3 + NH3のゴーストアトム
- NH3のみ
- NH3 + BF3のゴーストアトム
という4つのXYZ形式をエネルギー計算用に作成します.
def gen_coord(xyz_block):
lines = xyz_block.split('\n')
bf3 = ''''''
bf3_ghost = ''''''
nh3 = ''''''
nh3_ghost = ''''''
for i, line in enumerate(lines):
if i == 0:
bf3 += lines[i] + '\n'
bf3_ghost += lines[i] + '\n'
nh3 += lines[i] + '\n'
nh3_ghost += lines[i] + '\n'
elif i <= 4:
bf3 += lines[i] + '\n'
bf3_ghost += lines[i] + '\n'
nh3_ghost += '@' + lines[i][1:] + '\n'
elif i <= 8:
bf3_ghost += '@' + lines[i][1:] + '\n'
nh3 += lines[i] + '\n'
nh3_ghost += lines[i] + '\n'
return (bf3, bf3_ghost, nh3, nh3_ghost)
bf3, bf3_ghost, nh3, nh3_ghost = gen_coord(optimized_coord)
print(bf3)
print(bf3_ghost)
print(nh3)
print(nh3_ghost)
得られたXYZブロックはそれぞれ以下のようになります.元素記号の前の「@」に着目してください.
0 1 B -0.130832023738 0.000002057700 -0.000001939565 F -0.455764212348 -1.309645467737 -0.273141654611 F -0.455711786355 0.891376091949 -0.997633480457 F -0.455757590763 0.418294177575 1.270752994809 0 1 B -0.130832023738 0.000002057700 -0.000001939565 F -0.455764212348 -1.309645467737 -0.273141654611 F -0.455711786355 0.891376091949 -0.997633480457 F -0.455757590763 0.418294177575 1.270752994809 @N 1.546858460045 -0.000027893054 0.000025006159 @H 1.903403243253 0.935759128085 0.195084732226 @H 1.903367575271 -0.636852856790 0.712923905636 @H 1.903398085877 -0.299008729247 -0.907917531036 0 1 N 1.546858460045 -0.000027893054 0.000025006159 H 1.903403243253 0.935759128085 0.195084732226 H 1.903367575271 -0.636852856790 0.712923905636 H 1.903398085877 -0.299008729247 -0.907917531036 0 1 @B -0.130832023738 0.000002057700 -0.000001939565 @F -0.455764212348 -1.309645467737 -0.273141654611 @F -0.455711786355 0.891376091949 -0.997633480457 @F -0.455757590763 0.418294177575 1.270752994809 N 1.546858460045 -0.000027893054 0.000025006159 H 1.903403243253 0.935759128085 0.195084732226 H 1.903367575271 -0.636852856790 0.712923905636 H 1.903398085877 -0.299008729247 -0.907917531036
続いて作成した入力構造を用いてMP2/6-31G(d)レベルでエネルギー計算を行います.得られたエネルギー値を用いて
- 補正なしの相互作用エネルギー
- BSSE
- BSSEの補正を行った相互作用エネルギー
の3つの値を取得します.
e_bf3 = psi4.energy('mp2/6-31G(d)', molecule=psi4.geometry(bf3))
e_bf3_ghost = psi4.energy('mp2/6-31G(d)', molecule=psi4.geometry(bf3_ghost))
e_nh3 = psi4.energy('mp2/6-31G(d)', molecule=psi4.geometry(nh3))
e_nh3_ghost = psi4.energy('mp2/6-31G(d)', molecule=psi4.geometry(nh3_ghost))
int_energy = au2kcal * (e_total - (e_bf3 + e_nh3))
bsse_energy = au2kcal * ((e_bf3 + e_nh3) - (e_bf3_ghost + e_nh3_ghost))
print('Interaction energy w/o CP correction: {:.2f}'.format(int_energy))
print('BSSE at MP2/6-31G(d): {:.2f}'.format(bsse_energy))
print('Estimated interaction energy: {:.2f}'.format(int_energy + bsse_energy))
MP2/6-31G(d)レベルではBSSEが9.84 kcal/molであり,これを考慮すると先ほどと同じ40.10という相互作用エネルギーが得られました.
Interaction energy w/o CP correction: -49.94 BSSE at MP2/6-31G(d): 9.84 Estimated interaction energy: -40.10
結合エネルギー:分子の歪みエネルギーと相互作用エネルギーのバランス
相互作用前後の三フッ化ホウ素の構造を考えてみましょう.アンモニアとの相互作用がなければホウ素原子は平面三角形構造を取っているはずです.アンモニアとの相互作用が生じるにつれ,徐々にホウ素の平面性が崩れていき四面体構造へと遷移していくと考えられます.
先ほどのCP法で計算したモノマーのエネルギーは平面構造から歪んだ構造のエネルギーでした.会合体形成におけるエネルギーを考える場合には,下の図のように相互作用エネルギーだけでなく基底状態からの歪みエネルギーも考える必要があります.この場合,先ほど求めた安定化エネルギーは「歪みエネルギーと結合エネルギーの和」に相当します.

下記のコードでは三フッ化ホウ素とアンモニアについてそれぞれ独立にMP2/6-31G(d)で構造最適化を行うことで歪みエネルギーを求め,結合エネルギーを計算します.
bf3_opt = '''
0 1
B 0.49862748 0.06648936 0.00652739
F -0.23137252 1.33088645 0.00652739
F -0.23137252 -1.19790773 0.00652739
F 1.95862748 0.06648936 0.00652739
'''
nh3_opt = '''
0 1
N -0.37898936 -0.22606383 0.00000000
H -0.04566747 -1.16887691 0.00000000
H -0.04565026 0.24533635 0.81649673
H -0.04565026 0.24533635 -0.81649673
'''
e_bf3_opt = psi4.optimize('mp2/6-31G(d)', molecule=psi4.geometry(bf3_opt))
e_nh3_opt = psi4.optimize('mp2/6-31G(d)', molecule=psi4.geometry(nh3_opt))
e_dist = au2kcal * ((e_bf3 + e_nh3) - (e_bf3_opt + e_nh3_opt))
print('Interaction energy at MP2/6-31G(d): {:.2f}'.format(au2kcal * e_cpcorr + e_dist))
print('Distortion energy: {:.2f}'.format(e_dist))
この場合は歪みエネルギーが22.9 kcal/mol,結合エネルギーが17.2 kcal/molでした.
Interaction energy at MP2/6-31G(d): -17.16 Distortion energy: 22.94
このように原系と生成系や原系と遷移状態などのエネルギー差を,歪みエネルギーと相互作用エネルギーに分解して考察することで重要な化学的知見が得られることがあります.このような分析方法を「Activation Strainモデル」または「Distortion/Interaction分析」と呼びます.
興味のある方は以下の文献などを参照してみてください(オープンアクセスです).
"Analyzing Reaction Rates with the Distortion/Interaction‐Activation Strain Model"
Angew. Chem. Int. Ed. 2017, 56, 10070-10086.
基底関数系の大きさとBSSE
BSSEは基底関数系を大きくすることで小さくなると述べました.本節ではMP2を用いて,基底関数系を
- STO-3G
- 3-21G
- 6-31G(d)
- 6-31+G(dip)
- 6-311++G(2d,p)
- aug-cc-pVTZ
- aug-cc-pVQZ
と変化させていくことで実際にBSSEがどの程度小さくなるかを見てみましょう.
小さい分子ですがそれなりに時間がかかると思いますので,手許で実行する場合には計算リソースと相談して'aug-cc-pVQZ'を除くなどの処理を適宜行ってください.
import psi4
import time
now = time.strftime('%Y%m%d-%H%M')
psi4.set_num_threads(10)
psi4.set_memory('14GB')
psi4.set_output_file(now + '_BSSE_BStest.log')
au2kcal = psi4.constants.hartree2kcalmol
calc_energy = {}
bf3nh3 = '''
0 1
B -0.23097800 0.00000200 -0.00000200
F -0.54584700 -1.30452400 -0.27264200
F -0.54577900 0.88838500 -0.99344800
F -0.54583800 0.41616900 1.26606400
--
0 1
N 1.48202700 -0.00002600 0.00002300
H 1.83930300 0.93578300 0.19428800
H 1.83927700 -0.63617400 0.71333300
H 1.83929600 -0.29970200 -0.90754200
'''
bf3_opt = '''
0 1
B 0.49862748 0.06648936 0.00652739
F -0.23137252 1.33088645 0.00652739
F -0.23137252 -1.19790773 0.00652739
F 1.95862748 0.06648936 0.00652739
'''
nh3_opt = '''
0 1
N -0.37898936 -0.22606383 0.00000000
H -0.04566747 -1.16887691 0.00000000
H -0.04565026 0.24533635 0.81649673
H -0.04565026 0.24533635 -0.81649673
'''
basis_set = ['sto-3g', '3-21G', '6-31G(d)', '6-31+G(d,p)',
'6-311++G(2d,p)', 'aug-cc-pVTZ', 'aug-cc-pVQZ']
def opt_mol_with_theory(molecule, theory):
psi4_mol = psi4.geometry(molecule)
calc_energy = psi4.optimize(theory, molecule=psi4_mol)
optimized_coord = psi4_mol.save_string_xyz()
int_energy_with_cp = psi4.energy(theory, bsse_type='cp', molecule=psi4_mol)
return calc_energy, optimized_coord, int_energy_with_cp
def gen_coord(xyz_block):
lines = xyz_block.split('\n')
bf3 = ''''''
bf3_ghost = ''''''
nh3 = ''''''
nh3_ghost = ''''''
for i, line in enumerate(lines):
if i == 0:
bf3 += lines[i] + '\n'
bf3_ghost += lines[i] + '\n'
nh3 += lines[i] + '\n'
nh3_ghost += lines[i] + '\n'
elif i <= 4:
bf3 += lines[i] + '\n'
bf3_ghost += lines[i] + '\n'
nh3_ghost += '@' + lines[i][1:] + '\n'
elif i <= 8:
bf3_ghost += '@' + lines[i][1:] + '\n'
nh3 += lines[i] + '\n'
nh3_ghost += lines[i] + '\n'
return (bf3, bf3_ghost, nh3, nh3_ghost)
for bs in basis_set:
level_of_theory = 'mp2/' + bs
e_total, optimized_geom, e_cpcorr = opt_mol_with_theory(bf3nh3, level_of_theory)
bf3_coord, bf3_ghost_coord, nh3_coord, nh3_ghost_coord = gen_coord(optimized_geom)
e_bf3 = psi4.energy(level_of_theory, molecule=psi4.geometry(bf3_coord))
e_bf3_ghost = psi4.energy(level_of_theory, molecule=psi4.geometry(bf3_ghost_coord))
e_nh3 = psi4.energy(level_of_theory, molecule=psi4.geometry(nh3_coord))
e_nh3_ghost = psi4.energy(level_of_theory, molecule=psi4.geometry(nh3_ghost_coord))
int_energy = au2kcal * (e_total - (e_bf3 + e_nh3))
bsse_energy = au2kcal * ((e_bf3 + e_nh3) - (e_bf3_ghost + e_nh3_ghost))
e_bf3_opt = psi4.optimize(level_of_theory, molecule=psi4.geometry(bf3_opt))
e_nh3_opt = psi4.optimize(level_of_theory, molecule=psi4.geometry(nh3_opt))
e_dist = au2kcal * ((e_bf3 + e_nh3) - (e_bf3_opt + e_nh3_opt))
e_int = au2kcal * e_cpcorr + e_dist
calc_energy[bs] = (bsse_energy, e_cpcorr, e_dist, e_int)
得られた結果をまとめたものが以下の表になります.相互作用エネルギーはCP法によって補正した値です.
- 基底関数系を大きくすることでBSSEが小さくなっていること
- CP法を用いると小さな基底関数系を用いた場合でもかなり正確な値が算出できること
が確認できます.またSTO-3Gでは歪みエネルギーに比して相互作用エネルギーが小さいことがわかります.
| 基底関数系 | BSSE | 相互作用エネルギー | 結合エネルギー |
|---|---|---|---|
| STO-3G | 15.36 | -4.60 | 3.91 |
| 3-21G | 21.18 | -40.78 | -19.52 |
| 6-31G(d) | 9.84 | -40.10 | -17.16 |
| 6-31+G(d,p) | 6.90 | -44.18 | -19.85 |
| 6-311++G(2d,p) | 4.89 | -43.04 | -18.91 |
| aug-cc-pVTZ | 4.95 | -44.64 | -20.53 |
| aug-cc-pVQZ | 1.99 | -45.65 | -21.40 |
終わりに
今回は「Psi4で分子間相互作用エネルギーの計算:超分子法と基底関数重なり誤差」という話題について,
- 超分子法を用いた分子間相互作用エネルギーの求め方
- 基底関数重なり誤差とはなにか
- CP法を用いたBSSEの補正
- 歪みエネルギーと相互作用エネルギー
- Psi4によるCP法の使い方
などについて説明していきました.
今回は相互作用エネルギーの大きさについて着目しましたが,分子間相互作用のエネルギーの内訳がわかればその性質が理解できます.計算化学では「エネルギー分解法(EDA; Energy Decomposition Analysis)」と分類される各種計算方法によって相互作用エネルギーに対する静電力や分散力などの寄与を求めることができます.Psi4にはSAPTと呼ばれる計算方法が実装されており,簡便に用いることができます.
また今回はエネルギーの議論だけを行いましたが,反応の自由エネルギーなどを議論したい場合には振動数計算を行った上でそれら補正項を得る必要があります.
これまで「6-31G(d)」や「cc-pVTZ」などPsi4で最初から使える基底関数系のみを使ってきましたが,時には論文で発表された新しい基底関数系を使ってみたい場合もあるはずです.次回はそのような場合に利用するBasis Set Exchangeというデータベースについて触れたいと思います.
>>次の記事:「Basis Set Exchangeは基底関数系に関するデータベース:PythonとPsi4を用いてECPを自在に扱う」
コメント