計算手法とエネルギー・最適化構造の関係：コンフォメーション探索における注意点

「RDKitを用いたコンフォメーション探索：MMFFによる配座異性体生成とクラスタリング」という記事では，

RDKitに実装されているディスタンス・ジオメトリー法による配座発生
MMFFによる構造最適化と同一構造の除去
取得した多数のコンフォマーをDBSCANを用いてクラスタリング

という一連の作業を行い，コンフォマーを取得しました．

この過程では一貫してMMFFを用いてエネルギー評価を行ってきました．今回は用いる計算レベルによってエネルギーの値，ひいては最適化構造にどのような影響を与えるかを見ていきたいと思います．

本記事では量子化学計算エンジンとしてPsi4を用いています。本ブログのPsi4関係の記事は「Psi4の使い方」という記事にまとめています。参照してみてください。

本ブログではPythonのオープンソースライブラリであるPsi4を用いて，量子化学計算の初心者を対象にした記事を多数用意しています。記事の内容を一つずつ習得することで，知識・経験ゼロの状態から徐々にステップアップしていくことで，量子化学計算の基本コンセプトが習得できるように構成...

計算手法とポテンシャルエネルギー曲面の形
1. 構造最適化ができない例
  1. ポテンシャルエネルギー曲面の図示
  2. エネルギー極小値を求める
2. コンフォマー間のエネルギーの大小が異なる例
  1. Psi4を用いた制限付き構造最適化
  2. Psi4を用いて様々な計算レベルで構造最適化
エネルギー計算と構造最適化を異なる計算レベルで行う
終わりに

計算手法とポテンシャルエネルギー曲面の形

計算化学に馴染みのない人にありがちなのが「計算した構造だから正しい」と思い込んでしまうことです．

実際にはほぼ全ての分子についてシュレディンガー方程式は厳密には解けませんので，計算にあたって何らかの近似を行っています．どのような近似を行うかによって計算手法それぞれに特徴があり，ある手法では考慮できない相互作用なども存在します．

特に近年の量子化学計算における主流である密度汎関数法（DFT)では，分子軌道法とは異なり精度を上げるための理論的な道筋が明確でないこともあり，非常に多くの汎関数が開発されています．その様相は「Density Functional Theory Zoo」などと揶揄される程です．

一昔前は，「有機低分子はとりあえずB3LYPで最適化すれば大丈夫」といった風潮もありましたが，近年ではB3LYPでうまく評価できない系に関する知見も蓄積されてきたため，そのような「幻想」は消滅したように思います．一方で決定的なものは存在しないため，汎関数の選択は困難なままです．

構造最適化ができない例

まずはやや極端な例ですが，アルゴン二量体を取り上げてみます．このような希ガス二量体は分散力のみで安定化されているため，分散力を考慮できない計算手法では最適化構造を見出すことができません．

ポテンシャルエネルギー曲面の図示

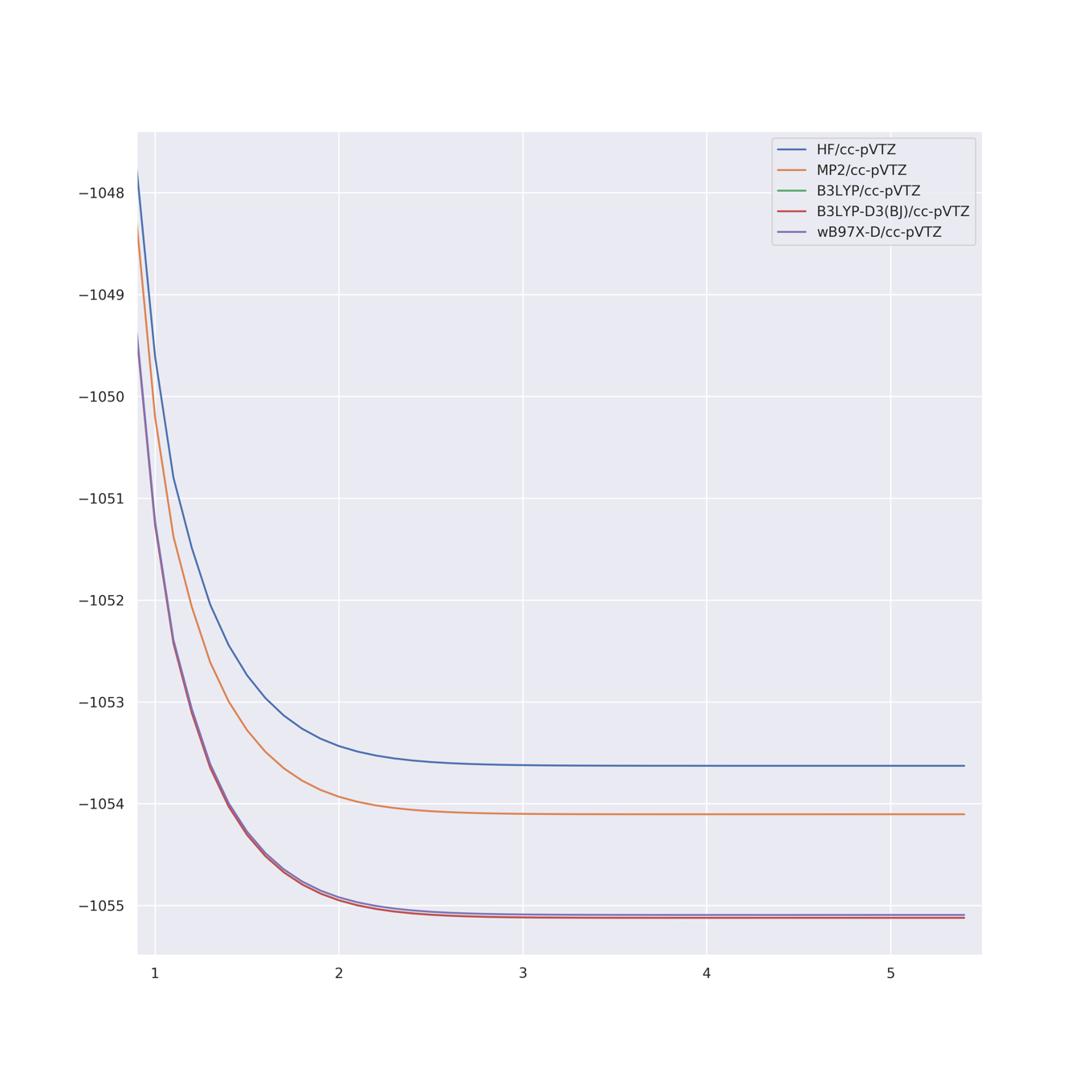
アルゴン–アルゴン間の距離を0.9から5.4Åまで変化させながらエネルギー計算を行っていくことでポテンシャルエネルギー曲面を描いてみましょう．

HF
MP2
B3LYP
B3LYP-D3(BJ)
wB97XD

の5つについて，cc-pVTZを基底関数系として計算することにします．

import psi4
print(psi4.__version__) # 1.3.2

# CPUとRAMは各自の環境に合わせて設定してください
psi4.set_num_threads(10)
psi4.set_memory('14GB')

ar_geom = '''
0 1
Ar  0 0 0
Ar  0 0 {}
'''

def calc_ar2_energy(level):
    theory = level + '/cc-pvtz'
    calc_energy = []
    for i in np.arange(0.9, 5.5, 0.1):
        ar2 = psi4.geometry(ar_geom.format(i))
        calc_energy.append(psi4.energy(theory, molecule=ar2))
    return calc_energy


hf = calc_ar2_energy('hf')
mp2 = calc_ar2_energy('mp2')
b3lyp = calc_ar2_energy('b3lyp')
b3lyp_d3bj = calc_ar2_energy('b3lyp-d3bj')
wb97x_d = calc_ar2_energy('wb97x-d')

得られたエネルギーをグラフ化したものが次のものになります．このままではエネルギーの極小値があるのかよくわかりません．

エネルギー極小値を求める

scipy.optimize.fminbound(f, x1, x2)

scipyには色々な最適化手法が実装されています．ここでは区間x1からx2の間の最小値を求めるoptimize.fminboundを使うことで，先ほどのエネルギー極小値を求めてみます．

下のコードではwB97X-Dの場合の極小値を求めています．

from scipy import optimize

def wb97xd_energy(r):
    ar2 = psi4.geometry(ar_geom.format(r))
    return psi4.energy('wb97x-d/cc-pvtz', molecule=ar2)

optimize.fminbound(wb97xd_energy, x1=1.0, x2=5.0)
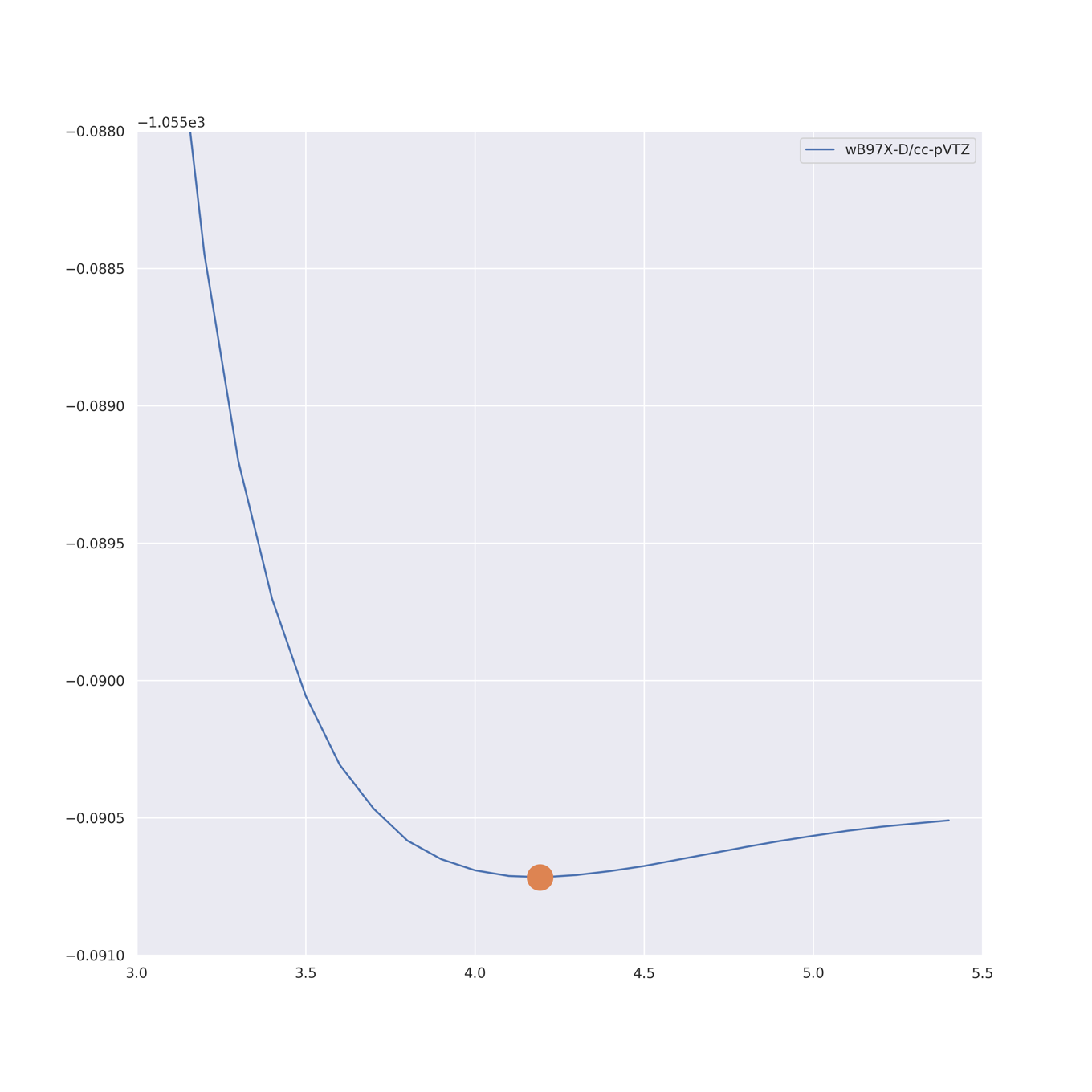
# 4.191968507707002

先ほどのグラフを実際に拡大してみると，確かに4.2Å付近で極小値を取っていることが確認できます．

同様にしてMP2とB3LYPで極小値を求めてみると，

MP2: 3.93358892716643，
B3LYP: 4.99999521993633

となりました．B3LYPは分散力を考慮できないため，区間[1.0,5.0]でエネルギーは単調減少となります．そのため4Å付近の極小値が存在せず構造最適化ができません．

コンフォマー間のエネルギーの大小が異なる例

続いて構造最適化は可能なものの，コンフォマー間のエネルギーの大小が異なる例を見てみます．「A sobering assessment of small‐molecule force field methods for low energy conformer predictions」という論文でもとりあげられているように，こちらのケースは非常に多く存在します．

1,2-ジフルオロエタンを例に，anti型とgauche型のエネルギーをいくつかの計算レベルで比べてみることとします．この分子は実験・理論の両面からよく研究されており，gauch型配座の方が安定であることがわかっています．

Psi4を用いた制限付き構造最適化

psi4.set_options({‘optking__fixed_dihedral’: ‘x1 x2 x3 x4 angle’})

まずは「RDKitを用いて制約付きで立体構造を生成する」で行ったような二面角をスキャンしながらの構造最適化を行ってみます．psi4の最適化モジュール「optking」のオプションで「fixed_dihedral」を用います．

注意点としては，このオプションでは指定する原子番号のカウントが1から始めます．pythonのように0からでない点に注意が必要です．

下記のコードではRDKitのコンフォマーオブジェクトの座標からPsi4のMoleculeオブジェクトを作成するためにgenXyzAngという関数を定義しています．

その上で，

RDKitを用いて分子を構築し，19のコンフォマーを発生
各コンフォマーに対して，0から180°までの二面角を対応させる
RDKitのコンフォマーオブジェクトの座標を用いてPsi4のMoleculeオブジェクトを作成
Psi4で二面角を固定しながらHF/STO-3Gで構造最適化

という処理を行っています．

from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, Descriptors
from rdkit.Chem.Draw import IPythonConsole
print(rdBase.rdkitVersion)
# 2019.09.3

mol = Chem.MolFromSmiles('FCCF')
mol = Chem.AddHs(mol)
confids = AllChem.EmbedMultipleConfs(mol, 19, AllChem.ETKDGv2())
len(confids) # 19

def genXyzAng(m, angle, confId=-1):
    conf = m.GetConformer(confId)
    Chem.rdMolTransforms.SetDihedralDeg(conf, 0,1,2,3, angle)

    xyz = '0 1'
    for atom, (x,y,z) in zip(m.GetAtoms(), conf.GetPositions()):
        xyz += '\n'
        xyz += '{}\t{}\t{}\t{}'.format(atom.GetSymbol(), x, y, z)

    return xyz


psi4.set_output_file('FCCF_HF.txt')

HF_FCCF = []
for i, angle in zip(confids, range(0,181,10)):
    conf = mol.GetConformer(i)
    Chem.rdMolTransforms.SetDihedralDeg(conf, 0, 1, 2, 3, angle)
    pmol = psi4.geometry(genXyzAng(mol, angle, i))
    # psi4による二面角の指定：1,2,3,4であることに注意
    psi4.set_options({'optking__fixed_dihedral': '1 2 3 4 {}'.format(angle)})
    psi4.set_options({'geom_maxiter': 200})
        
    e = psi4.optimize('hf/sto-3g', molecule=pmol)
    HF_FCCF.append(e)

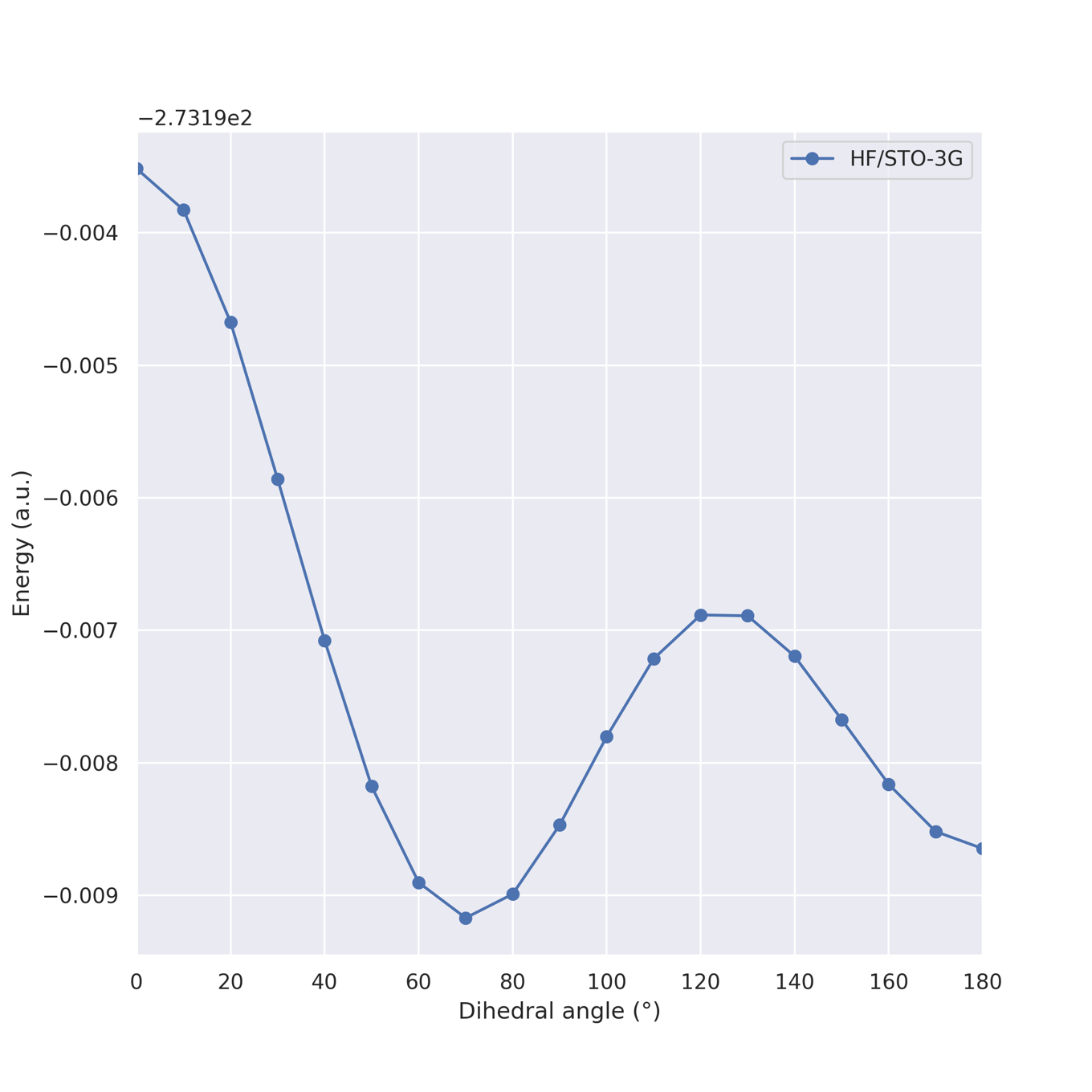
得られたエネルギーをプロットしたものが下のグラフです．これから，HF/STO-3Gレベルにおいては

anti型とgauche型2つのコンフォマーがあること
この計算レベルではgauche型の方が安定であること
gauche型は70°あたりが最適構造であること

などが見てとれます．

Psi4を用いて様々な計算レベルで構造最適化

続いて二面角60°と180°を初期構造として様々な計算手法で構造最適化を行い，anti型とgauche型のエネルギー差を比べてみます．

具体的には

HF, MP2, B3LYP, B3LYP-D3(BJ)
STO-3G, 6-31G(d), 6-31+G(d,p), 6-311+G(2d,p)

の組合せで4 x 4通りの計算レベルについて調べてみます．

また

GetSubstructMatchを利用して二面角の指定範囲をmatchとして取得，設定
最適化したPsi4のMoleculeオブジェクトの座標をRDKitのコンフォマーへと移すpsi2conf関数を定義

することで，一般性の向上と最適化後の二面角の取得を行っています．最適化後の座標を含んだMOLファイルも保存しておきます．

なおpsi4.Moleculeオブジェクトから(x,y,z)座標を取り出す際，単位がBohrになっていますのでpsi4.constants.bohr2angstromsを用いて変換しています．

from datetime import datetime
import itertools

smiles = 'FCCF'
pattern = Chem.MolFromSmarts('FCCF')
theory = ['hf', 'mp2', 'b3lyp', 'b3lyp-d3bj']
basis = ['sto-3g', '6-31G(d)', '6-31+G(d,p)', '6-311+G(2d,p)']
angles = [60, 180]


def mol2conf(sm, angle):
    # sm: smiles, angle: dihedral angle to be set in the conformer
    mol = Chem.MolFromSmiles(sm)
    mol = Chem.AddHs(mol)
    _ = AllChem.EmbedMolecule(mol)
    match = mol.GetSubstructMatch(pattern)
    conf = mol.GetConformer(-1)
    Chem.rdMolTransforms.SetDihedralDeg(conf, *match, angle)

    return mol, conf


def conf2xyz(mol, conf):
    # mol: rdkit mol, conf: conformer of mol
    xyz = '0 1'
    for atom, (x, y, z) in zip(mol.GetAtoms(), conf.GetPositions()):
        xyz += '\n'
        xyz += '{}\t{}\t{}\t{}'.format(atom.GetSymbol(), x, y, z)

    return xyz


def psi4_optimize(th, ba, xyz):
    # th: theory, ba: basis set, xyz: coordinate
    psi4.set_module_options('optking', {'geom_maxiter': 200})
    psimol = psi4.geometry(xyz)
    energy = psi4.optimize(th + '/' + ba, molecule=psimol)

    return energy, psimol


def psi2conf(psimol, conf):
    # mol: psi4 mol, conf: conformer of rdkit mol
    for i in range(psimol.natom()):
        x = psimol.x(i) * psi4.constants.bohr2angstroms
        y = psimol.y(i) * psi4.constants.bohr2angstroms
        z = psimol.z(i) * psi4.constants.bohr2angstroms
        conf.SetAtomPosition(i, (x, y, z))


results = []
for (angle, th, ba) in itertools.product(angles, theory, basis):
    print('--')
    print('{}/{} with {}deg'.format(th, ba, angle))
    mol, conf = mol2conf(smiles, angle)
    geom = conf2xyz(mol, conf)
    match = mol.GetSubstructMatch(pattern)

    now = datetime.now()
    log_file = '{}_{}_{}.txt'.format(datetime.strftime(now, '%y%m%d_%H%M'), th, ba[:5])
    psi4.set_output_file(log_file)

    energy, psimol = psi4_optimize(th, ba, geom)
    psi2conf(psimol, conf)
    final_angle = Chem.rdMolTransforms.GetDihedralDeg(conf, *match)

    mol = Chem.RemoveHs(mol)
    Chem.MolToMolFile(mol, '{}_{}_{}_{}deg.txt'.format(th, ba[:5], smiles, angle))

    results.append((smiles, angle, th, ba, energy, final_angle))

with open('./result.txt', 'w') as f:
    print(results, file=f)

計算レベル毎のgauch型とanti型のエネルギー差は以下のようになりました．なお最適化構造の二面角は，anti型では179.5から180.0°とほとんど変化がなかったのに対し，gauche型は69.0から72.4°と計算手法による違いが大きかったです．

HF/STO-3Gではgauche型の方が安定になっていますが，より大きい基底関数系を用いるとanti型の方が安定になっています．この結果は他の計算レベルでの結果を踏まえると，

HFを用いるとうまく評価できないエラー
最小基底系では評価できないエラー

がキャンセルしあって偶然出てきた結果であると結論付けられそうです．

計算手法	エネルギー差 (kcal/mol)
HF/STO-3G	-0.3290318484135456
HF/6-31G(d)	0.45126090174887473
HF/6-31+G(d,p)	0.1304722850608613
HF/6-311+G(2d,p)	-0.30009113129279874
MP2/STO-3G	-0.3584640475723512
MP2/6-31G(d)	-0.21332636897446614
MP2/6-31+G(d,p)	-0.4833678449151578
MP2/6-311+G(2d,p)	-0.8516391230649175
B3LYP/STO-3G	-0.3677167585435006
B3LYP/6-31G(d)	-0.3728175376350604
B3LYP/6-31+G(d,p)	-0.6567267035116128
B3LYP/6-311+G(2d,p)	-0.8938457404183217
B3LYP-D3(BJ)/STO-3G	-0.373095195655657
B3LYP-D3(BJ)/6-31G(d)	-0.3839035364556454
B3LYP-D3(BJ)/6-31+G(d,p)	-0.6666511601584338
B3LYP-D3(BJ)/6-311+G(2d,p)	-0.9046106549686137