計算化学の構造最適化の基本をPsi4で学ぶ

「計算化学にPythonとPsi4で入門」という記事ではpythonで扱える量子化学計算ソフトウェア「Psi4」の紹介と，簡単なエネルギー計算のやり方を扱いました．

その際に得られるエネルギーは

用いる計算レベルによってエネルギーの値が異なる
計算する構造によってエネルギーの値が異なる

ということを確認しました．

そしてエネルギーが分子の自由度を変数とした関数であることから，徐々にエネルギーが小さくなるように構造を変化させていくことで安定構造へと導くことができる，すなわち構造最適化計算が行えることを述べました．

今回はこの点を掘り下げていき，どのようにしてpsi4で構造最適化計算を行っていくかを，注意点とともに説明していきたいと思います．

本ブログのPsi4関係の記事は「Psi4の使い方」という記事にまとめています。参照してみてください。

【まとめ】Psi4の使い方

本ブログではPythonのオープンソースライブラリであるPsi4を用いて，量子化学計算の初心者を対象にした記事を多数用意しています。記事の内容を一つずつ習得することで，これから計算化学を始めたい人が知識・経験ゼロの状態から徐々にステップアップしていくことで，量子化学計算の基本コ...

計算に用いる3次元入力構造の取得
Psi4を用いた構造最適化計算
構造最適化の終了判定
最適化構造の取得
構造最適化計算における初期構造の大切さ
終わりに

計算に用いる3次元入力構造の取得

「計算化学にPythonとPsi4で入門」という記事で例とした水分子のような単純分子ならエディタだけで記述することも容易です．しかし一般的に計算に用いるような，より大きな分子系の構築にはモデリングソフトを使う方が楽ですし，ミスが少なくなります．

GaussViewなどの有償ソフトウェアが使える環境なら，普段から慣れたものを使うのがよいでしょう．無償で利用可能なモデリングソフトとしては，例えば，AvogadroやwxMacMolPltが挙げられます．後者はGAMESS用の機能が充実してますが，分子の構築だけなら特に計算ソフトウェアに関わらず使えます．

またSMILESやSDFなどからpython用のケモインフォマティクスライブラリーであるRDKitを用いて３次元構造を発生させて，各原子の3次元座標を取得することも可能です．多数の分子を扱いたい場合には，こちらの方法で自動化する方が現実的だと思います．

RDKitのMolオブジェクトから3次元座標を取得する方法については，「RDKitによるコンフォマーの生成」という記事で解説しています．参照してみてください．

今回の例ではAvogadroを用いてm-キシレンのモデリングを行いました．

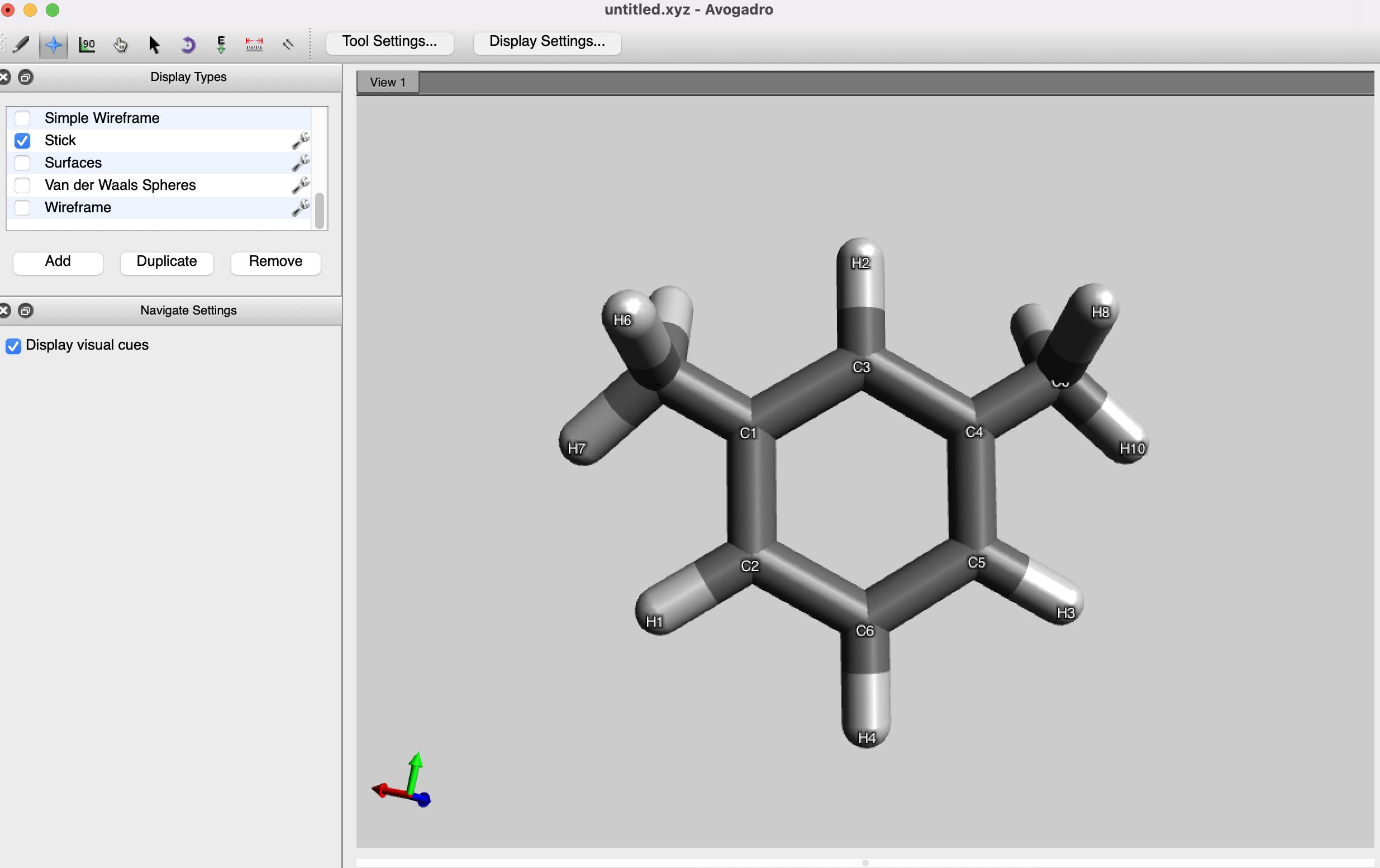
MOLファイルまたはXYZ形式で保存することで座標情報が取得できます．またAvogadroはPsi4をはじめとする各種量子化学計算ソフトの入力ファイル作成支援機能が付属しています．

例えばPsi4形式での入力ファイル画面を選択してみると以下のようになります．出力される入力ファイルは「計算化学にPythonとPsi4で入門」という記事で説明したPsithon形式のファイルですが，分子構造の指定形式は共通ですので青枠で囲んだ部分をコピーすることで利用可能です．

MOLファイルについては「MOLファイル・SDFとはどんな化学情報ファイルなのか？」という記事で，XYZ形式については「XYZ形式とZ-マトリックスは分子の立体構造を表す入力フォーマット」という記事でそれぞれ解説しています．参照してみてください．

Psi4を用いた構造最適化計算

psi4.optimize(level, molecule)

Psi4を用いた構造最適化計算はエネルギー計算の「energy」を「optimize」に変更するだけで可能です．

以下のコードはAvogadroを用いて取得したm-キシレンの座標を使って，

計算環境の設定
分子構造の設定（m-キシレン）
計算手法の設定（HF/STO-3Gによる構造最適化計算）

を行っています．

import psi4
import sys
import os
import datetime

file_name = sys.argv[0]
file, _ = os.path.splitext(file_name)
now = datetime.datetime.now()

logfile = file + '_{}{}{}_{}{}.log'.format(now.year, now.month, now.day, now.hour, now.minute)

psi4.set_num_threads(nthread=2)
psi4.set_memory('4GB')
psi4.set_output_file(logfile)

m_xylene = psi4.geometry('''
0 1
H          1.28968       -0.58485        2.54537
C          0.72665       -0.53821        1.60812
C         -0.66059       -0.63788        1.62278
H         -1.18866       -0.76325        2.57379
C         -1.38281       -0.57923        0.43824
H         -2.47598       -0.65808        0.46597
C         -0.70870       -0.41532       -0.78014
C         -1.44994       -0.24691       -1.99137
C          0.68999       -0.31852       -0.79417
H          1.23196       -0.19170       -1.73873
C          1.39668       -0.37916        0.39958
C          2.48879       -0.30069        0.38763
H         -2.49493       -0.35404       -1.78784
H         -1.14694       -0.98824       -2.70096
H         -1.26259        0.72757       -2.39162
H          2.86211       -0.36704        1.38820
H          2.77426        0.63858       -0.03801
H          2.89720       -1.09694       -0.19896
''')

psi4.optimize('hf/sto-3g', molecule=m_xylene)

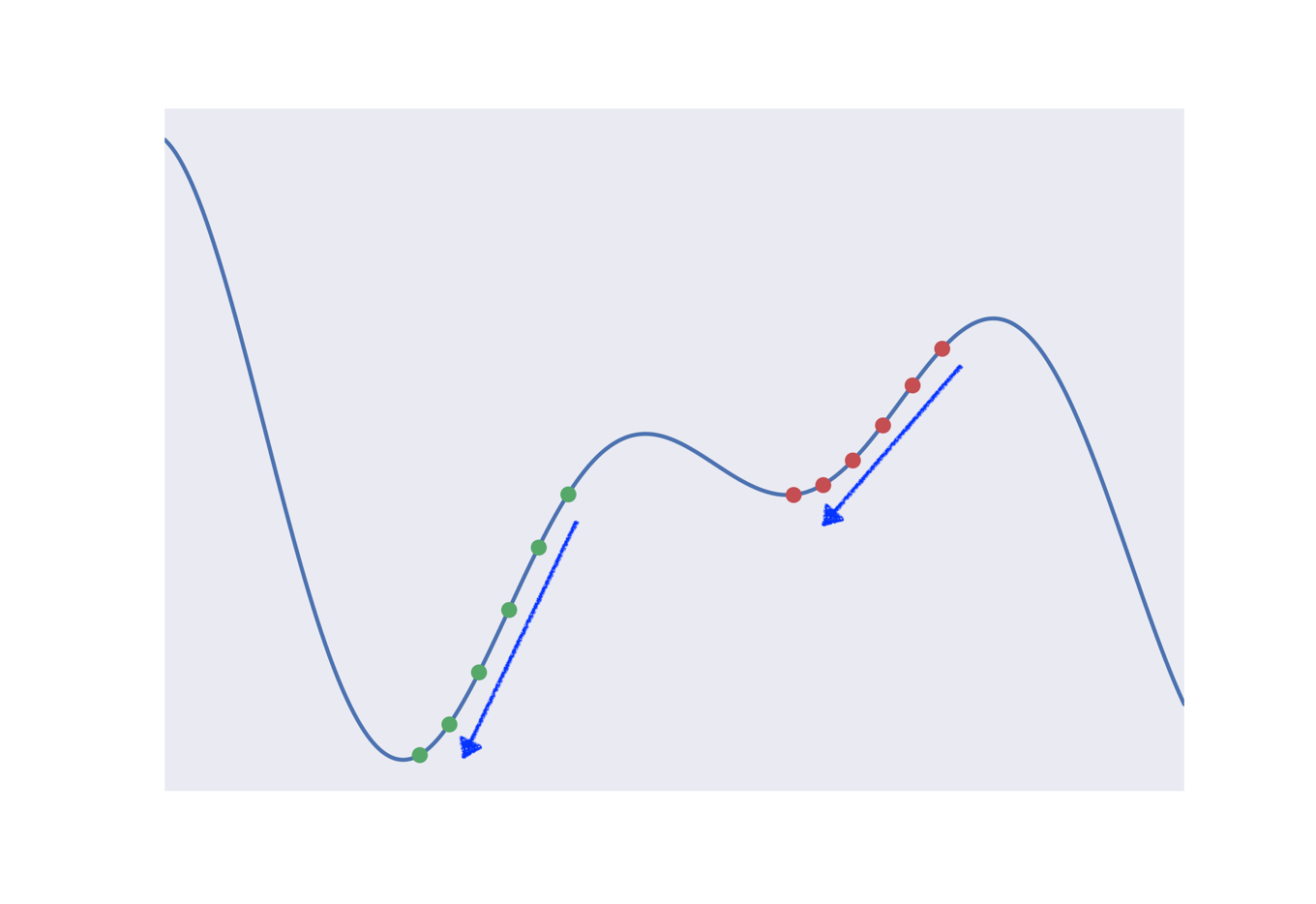
構造最適化計算では，分子構造を徐々に変化させながらエネルギーの低い安定構造を目指していきます．実際には分子の自由度（3N-6）を変数とした超次元空間中での最適化ですが，簡単のために下のようなグラフがよく説明に使われます．横軸が構造，縦軸がエネルギーです．丸点が各最適化ステップを表しています．

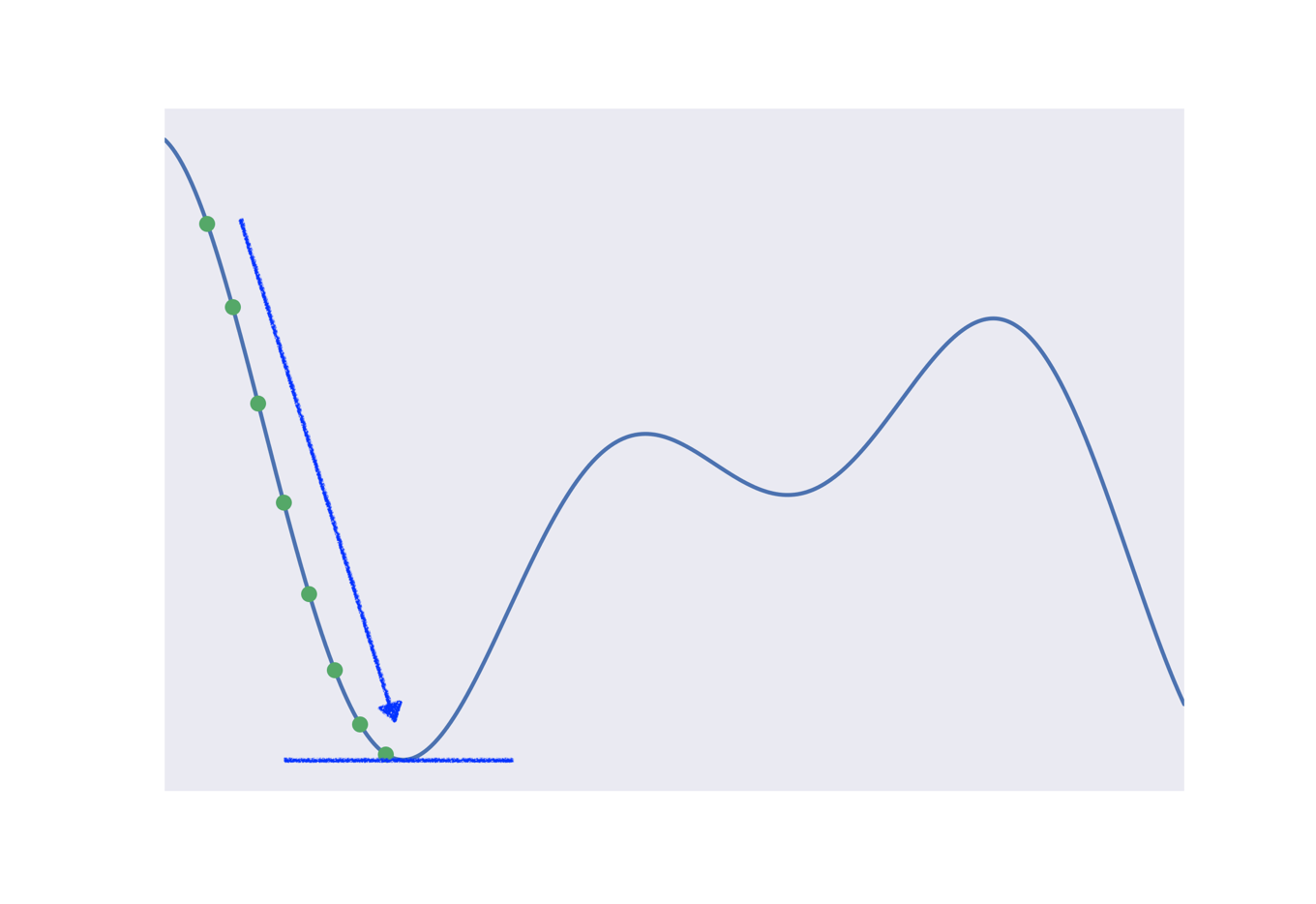
コンピュータによる最適化では必ずしも解析的な極小値（上のグラフの青の水平線）には辿り着きません．代わりにいくつかの指標を用いて極小値に十分近いことを保証します．

具体的には

エネルギー変化の絶対値
エネルギー勾配（エネルギーの微分，フォース）
構造変化における原子位置の変化

などを考慮していき，予め定めた基準に達した際に最適化が終了したと判定します．

ログファイルによると今回の計算では８回目の最適化ステップにおいて，

Delta E
MAX Force
MAX Dips (displacement)

が基準値に達しました（*がつきました）．その後に各ステップにおけるエネルギー値などの一覧が出力されています．

  ==> Convergence Check <==

  Measures of convergence in internal coordinates in au.
  Criteria marked as inactive (o), active & met (*), and active & unmet ( ).
  ---------------------------------------------------------------------------------------------
   Step     Total Energy     Delta E     MAX Force     RMS Force      MAX Disp      RMS Disp
  ---------------------------------------------------------------------------------------------
    Convergence Criteria    1.00e-06 *    3.00e-04 *             o    1.20e-03 *             o
  ---------------------------------------------------------------------------------------------
      8    -305.06086184   -3.33e-07 *    5.76e-05 *    1.61e-05 o    1.14e-03 *    2.83e-04 o  ~
  ---------------------------------------------------------------------------------------------


  **** Optimization is complete! (in 8 steps) ****

  ==> Optimization Summary <==

  Measures of convergence in internal coordinates in au.
  --------------------------------------------------------------------------------------------------------------- ~
   Step         Total Energy             Delta E       MAX Force       RMS Force        MAX Disp        RMS Disp  ~
  --------------------------------------------------------------------------------------------------------------- ~
      1    -304.755052587477   -304.755052587477      1.01541269      0.11213460      0.44157178      0.05335275  ~
      2    -305.020608964134     -0.265556376657      0.23704913      0.02628564      0.13962280      0.02122282  ~
      3    -305.047180802035     -0.026571837901      0.12650915      0.01387954      0.15666687      0.01864962  ~
      4    -305.059405379085     -0.012224577050      0.03434785      0.00388252      0.05081476      0.00878295  ~
      5    -305.060685308605     -0.001279929520      0.01192491      0.00134848      0.02184944      0.00279314  ~
      6    -305.060850955290     -0.000165646685      0.00276301      0.00032505      0.00622531      0.00125076  ~
      7    -305.060861504101     -0.000010548811      0.00021564      0.00004516      0.00246837      0.00067572  ~
      8    -305.060861837100     -0.000000332999      0.00005765      0.00001613      0.00114045      0.00028315  ~
  --------------------------------------------------------------------------------------------------------------- ~

構造最適化の終了判定

'G_CONVERGENCE': 'QCHEM'

先ほどの最適化計算においては，

Delta E
MAX Force
MAX Dips (displacement)

の３つが最適化計算の終了判定に使われていました．これら終了判定基準はG_CONVERGENCEオプションによって設定可能です．例えばGaussianなどの他の量子化学計算ソフトウェアで用いられる判定基準と同じものを設定可能です．

下の表にはGaussianの各種設定と，Molpro，Q-Chem（デフォルト）の値をまとめておきました．その他のオプションの詳細は公式ドキュメント「Convergence Criteria」を参照してください．

なおPsi4でQ-Chemの値がデフォルトになっているのはDavid SherrillがMartin Head-Gordon一派で，Q-Chemにも関わっているからでしょう．

G_CONVERGENCE	Max Energy	Max Force	RMS Force	Max Disp	RMS Disp
GAU_LOOSE		2.5×10⁻³	1.7×10⁻³	1.0×10⁻²	6.7×10⁻³
GAU		4.5×10⁻⁴	3.0×10⁻⁴	1.8×10⁻³	1.2×10⁻³
QCHEM（デフォルト）	1.0×10⁻⁶	3.0×10⁻⁴		1.2×10⁻³
MOLPRO	1.0×10⁻⁶	3.0×10⁻⁴		3.0×10⁻⁴
GAU_TIGHT		1.5×10⁻⁵	1.0×10⁻⁵	6.0×10⁻⁵	4.0×10⁻⁵
GAU_VERYTIGHT		2.0×10⁻⁶	1.0×10⁻⁶	6.0×10⁻⁶	4.0×10⁻⁶

なお厳しい終了判定基準を採用すれば，

計算時間が長くなる
そもそも最適化が終了しないこともありえる

ということを頭に入れておいてください．いたずらに厳格な基準を採用するのではなく，求めたい構造の特徴に応じて基準を変えることが大切です．

最適化構造の取得

Molecule.geometry()
Molecule.to_arrays()
Molecule.save_string_xyz()
Molecule.symbol(idx)
Molecule.x(idx)

psi4では構造最適化後には，分子の構造は最適化構造にアップデートされます．最適化構造の原子座標はログファイルにも記されていますが，psi4のMoleculeオブジェクトからも取得可能です．

注意点としては利用するメソッドによって，得られる座標の単位がボーアの場合とオングストロームの場合があります．前者から後者への変換はpsi4.constants.bohr2angstromsという定数が用意されています．

Psi4.Matrixオブジェクト

geometryメソッドではpsi4のMatrixオブジェクトで座標情報が取得されます．これを例えばnumpyのarrayに変えることでその後の利用が容易になります．こちらは単位はボーアです．

import numpy as np
x = m_xylene.geometry()
y = np.array(x)
print(y)

array([[ 1.97257588, -0.43873574,  4.6764138 ],
       [ 0.94773222, -0.29060133,  2.91326433],
       [-1.66505613, -0.44864943,  2.90601712],
       [-2.67326095, -0.72004501,  4.66584467],
       [-2.99432905, -0.26281037,  0.65882074],
       [-5.03511572, -0.38857441,  0.6687015 ],
       [-1.71917012,  0.08644586, -1.61243804],
       [-3.1524049 ,  0.30381249, -4.10857183],
       [ 0.90375836,  0.24185695, -1.57747831],
       [ 1.91182373,  0.51299279, -3.33672867],
       [ 2.26225211,  0.05767162,  0.66465756],
       [ 5.14308787,  0.23690136,  0.63418298],
       [-5.16745785,  0.06093551, -3.81760147],
       [-2.51458245, -1.12321631, -5.44237083],
       [-2.84259279,  2.14496415, -4.96824665],
       [ 5.90637483,  0.05776423,  2.52882038],
       [ 5.75294897,  2.04038771, -0.13997094],
       [ 5.95330102, -1.24902143, -0.53173817]])

XYZ形式での書き出し

XYZ形式での書き出しはいくつかのメソッドがありますが，例えばsave_string_xyzでは１行目が「電荷　スピン多重度」という形式での出力になります．こちらの座標の単位はオングストロームで，すぐに他の計算に利用可能な出力形式になっています．

0 1
 H    1.043842196389   -0.232168952475    2.474651600664
 C    0.501518291947   -0.153779601479    1.541633087031
 C   -0.881109752569   -0.237415052400    1.537798027016
 H   -1.414628766189   -0.381031408561    2.469058656462
 C   -1.584530685842   -0.139073259267    0.348632920822
 H   -2.664468483928   -0.205624720408    0.353861591551
 C   -0.909745644608    0.045745180129   -0.853265459788
 C   -1.668180827898    0.160770646663   -2.174162572957
 C    0.478248323888    0.127985187407   -0.834765571240
 H    1.011693546122    0.271464090197   -1.765720763430
 C    1.197132254959    0.030518506752    0.351721633902
 C    2.721604882168    0.125362802971    0.335595180400
 H   -2.734500923110    0.032245683764   -2.020187691744
 H   -1.330659722770   -0.594380470426   -2.879978604912
 H   -1.504235316387    1.135066143893   -2.629082894934
 H    3.125518944169    0.030567512456    1.338194108564
 H    3.044329479355    1.079726672898   -0.074069433204
 H    3.150351216441   -0.660953673506   -0.281383722335

原子番号を用いた座標構造の取得

Molecule.natomで原子の数がわかりますので，それを原子IDとして用いることで各原子の元素記号や座標が取得できます．この方法も単位はボーアです．

for n in range(m_xylene.natom()):
    x_p, y_p, z_p = m_xylene.x(n), m_xylene.y(n), m_xylene.z(n)
    print('{}\t{:.2f}\t{:.2f}\t{:.2f}'.format(m_xylene.symbol(n),x_p,y_p,z_p))

H   1.97    -0.44   4.68
C   0.95    -0.29   2.91
C   -1.67   -0.45   2.91
H   -2.67   -0.72   4.67
C   -2.99   -0.26   0.66
H   -5.04   -0.39   0.67
C   -1.72   0.09    -1.61
C   -3.15   0.30    -4.11
C   0.90    0.24    -1.58
H   1.91    0.51    -3.34
C   2.26    0.06    0.66
C   5.14    0.24    0.63
H   -5.17   0.06    -3.82
H   -2.51   -1.12   -5.44
H   -2.84   2.14    -4.97
H   5.91    0.06    2.53
H   5.75    2.04    -0.14
H   5.95    -1.25   -0.53

異なる判定基準を用いた場合の構造

'GEOM_MAXITER': 50

それでは少し終了判定基準を変化させてm-キシレンの最適化を行ってみたいと思います．その際に一部の方法ではデフォルトの最適化ステップ数50では安定構造に落ち着きませんので，GEOM_MAXITERオプションを設定することで，最適化ステップの回数を増やしています．

Q-Chem，Gaussian，Molproの判定基準で最適化を行いました．

geom = '''
0 1
H          1.28968       -0.58485        2.54537
C          0.72665       -0.53821        1.60812
C         -0.66059       -0.63788        1.62278
H         -1.18866       -0.76325        2.57379
C         -1.38281       -0.57923        0.43824
H         -2.47598       -0.65808        0.46597
C         -0.70870       -0.41532       -0.78014
C         -1.44994       -0.24691       -1.99137
C          0.68999       -0.31852       -0.79417
H          1.23196       -0.19170       -1.73873
C          1.39668       -0.37916        0.39958
C          2.48879       -0.30069        0.38763
H         -2.49493       -0.35404       -1.78784
H         -1.14694       -0.98824       -2.70096
H         -1.26259        0.72757       -2.39162
H          2.86211       -0.36704        1.38820
H          2.77426        0.63858       -0.03801
H          2.89720       -1.09694       -0.19896
'''

def optimization_xylene(F):
    psi4.set_options({'geom_maxiter': 100})
    psi4.set_options({'g_convergence': F})
    xylene = psi4.geometry(geom)
    psi4.optimize('hf/sto-3g', molecule=xylene)
    return xylene

qchem = optimization_xylene('qchem')
gau = optimization_xylene('gau')
molpro = optimization_xylene('molpro')

得られた構造のRMS値は以下のようになりました．同じ構造から最適化を始めても，終了判定条件を変えることで収束した最適化構造に多少の違いが生じることがわかります．

	Q-Chem	Gaussian	Molpro
Q-Chem	0	0.0002837	0.0058563
Gaussian	0.0002837	0	0.0056917
Molpro	0.0058563	0.0056917	0

構造最適化計算における初期構造の大切さ

先ほど最適化計算の終了判定について説明する際に，「いくつかの指標を用いて極小値に十分近いことを保証します」と記しました．

実は構造最適化計算では必ずしも最安定構造に辿り着くことは保証されていません．下の図を見てみてください．緑の点から最適化を始めた場合には安定構造に辿り着きますが，赤い点から計算を始めた場合には（多くの場合）局所的な安定構造に落ち着いてしまいます．

すなわち，初期構造を適切に選択することが非常に大切になります．現実的にはいろいろな構造から始めてどの構造が最安定かを計算することが多いです．

以下の例ではブタンの「アンチ配座」と「ゴーシュ配座」を例にしてこのことを確認してみましょう．上の例と同じく，Avogadroを用いて構造を作成しました．

アンチ配座	ゴーシュ配座

anti = psi4.geometry('''
0 1
C         -4.17385        0.37732        0.00000
C         -3.10385        0.37732        0.00000
H         -4.53051        1.24338       -0.51734
H         -4.53052        0.39232        1.00869
C         -4.53052       -0.50373       -0.49135
C         -2.74719        1.25838        0.49135
H         -2.74718        0.36232       -1.00869
H         -2.74718       -0.48873        0.51734
H         -3.10386        2.12443       -0.02599
H         -1.67719        1.25838        0.49135
H         -3.10385        1.27338        1.50005
H         -4.17385       -0.51873       -1.50005
H         -5.60052       -0.50373       -0.49135
H         -4.17386       -1.36979        0.02599
''')

gauche = psi4.geometry('''
0 1
C         -2.25507        0.85394        0.00000
C         -1.18507        0.85394        0.00000
C         -2.61173        1.26615       -0.92075
H         -2.61173        1.44522        0.81736
H         -2.61174       -0.14955        0.10339
C         -0.82840        1.85743       -0.10339
H         -0.82840        0.26265       -0.81736
H         -0.82840        0.44173        0.92074
H         -1.18508        2.26964       -1.02414
H          0.24160        1.85744       -0.10339
H         -1.18507        2.44872        0.71397
H         -2.25506        2.26964       -1.02413
H         -3.68173        1.26615       -0.92075
H         -2.25506        0.67486       -1.73810
''')

e_anti = psi4.optimize('hf/sto-3g', molecule=anti)
e_gauche = psi4.optimize('hf/sto-3g', molecule=gauche)

print('Anti conformer: {:.5f}\tGauche conformer: {:.5f}'.format(e_anti, e_gauche))

最適化計算はアンチ配座が13ステップ，ゴーシュ配座が30ステップで終了し，最適化後のエネルギーは以下のように出力されました．予想通りにアンチ配座の方が安定と計算されました．

なおこのように異性体間のエネルギーを比べる際には計算レベルを揃える（今回はHF/STO-3G）必要があることに注意してください．

Anti conformer: -155.46716  Gauche conformer: -155.46583

終わりに

今回は「計算化学の構造最適化の基本をPsi4で学ぶ」という話題について，

構造最適化計算の基本的な考え方
計算の終了判定について
初期構造の大切さについて

などについて，具体的にPsi4を用いて計算を行いながら触れました．

次回は計算レベルを変えることによるエネルギーや最適化構造に与える影響について触れたいと思います．

＞＞次の記事：「計算手法とエネルギー・最適化構造の関係：コンフォメーション探索における注意点」