RDKitでランダムフォレスト：機械学習でも「みんなの意見」は案外正しい

「scikit-learnの決定木でAmes試験データセットを機械学習」という記事では「決定木」と呼ばれる手法について説明しました．決定木は

• モデルの可視化が容易
• その内容が理解しやすい
• 特徴量の前処理を必要としない

といった長所がありました．一方で決定木は，

• 容易に過剰適合を起こす
• データの小さな変化でモデルが大きく変わることがある

などといった欠点も知られています．

今回は決定木のこういった欠点を克服するための方法として，複数の決定木を組み合わせることを考えます．複数の機械学習モデルを組み合わせることを一般に「アンサンブル法」と呼びますが，今回は特に「ランダムフォレスト」と呼ばれる手法を扱います．

アンサンブル学習とは

「群衆の英知」という言葉を聞いたことがあるでしょうか？もともとは社会学や心理学方面での考えかただったようです．Web2.0という言葉が流行った2005年頃，日本だと梅田望夫氏の『ウェブ進化論』やジェームズ・スロウィッキーの『「みんなの意見」は案外正しい』（The Wisdom of Crowds）といった本によって（ITに興味のある）一般の人にも広められた考え方だと思います．

要点は「多様性のある個人の集団が，各々独立して下す判断を集めると，専門家の判断にも勝る」などとまとめられます．似たもの同士の集まるFacebookやtwitterのタイムラインが選挙結果を占う世論調査にはならないように，「多様性」と「独立」が重要です．

機械学習の文脈でも同様のことが言えることがわかっています．すなわち，1つ1つのモデルは精度が低くても（弱い学習機，weak learner），そういったモデルを複数組み合わせることで全体の精度を向上させることが可能になります．これを「アンサンブル学習」と呼び，そのためには各モデル間の「多様性」と「独立」を維持することが大切になります．

アンサンブルの手法としては以下の3通りが主な方法になります．

• バギング（bagging）
• ブースティング（boosting）
• スタッキング（stacking）

後者2つについては別の機会で触れることとし，ここでは「バギング」について説明します．その後，バギングを用いて決定木を重ね合わせた「ランダムフォレスト」を見ていきます．

バギングとは

バギング（bagging）とは「bootstrap aggregating」を略したもので，文字通りブートストラップサンプリングを重ね合わせたものです．

先に述べたようにアンサンブル学習の効果を発揮するためには，複数の多様なモデルを構築する必要があります．そのための最も簡単な方法は「異なるアルゴリズムを用いたモデルを複数集めること」でしょう．アルゴリズムによって学習できる特徴やエラーの様相が異なりますので，必然的に多様なモデルが集まります．

別の方法としては，「同じ訓練アルゴリズムを異なるデータセットに対して用いる」ことで多様性を生み出すことができます．手元にある訓練用のデータ数は決まっていますので，その一部分をランダムに選んだデータセットを用いてモデル構築を行います．その際に復元抽出（重複を許可）で部分サンプリングを行うことを「ブートストラップサンプリング」と言います．

つまりバギングとはブートストラップサンプリングで作成されたデータセットに対して訓練された複数のモデルを集めることで判断を下すアンサンブル学習法になります．

バギングのscikit-learnにおける実装

バギングを用いた分類機はensemble.BaggingClassifierで実装されています．以下で示すランダムフォレストは決定木のモデルを組み合わせたものですが，こちらのBaggingClassifierを用いることで，いかなるモデルを基にしてもバギングを用いたアンサンブル学習が可能になります．

ランダムフォレストとは

ここまで述べてきたように，ランダムフォレストとは（通常は）バギングを用いて決定木モデルを多数作成するアンサンブル学習法になります．

決定木の

• 容易に過剰適合を起こす
• データの小さな変化でモデルが大きく変わることがある

といった欠点を克服する強力な機械学習法で，「分類」「回帰」を問わず幅広く使われています．1つ欠点を挙げると，決定木ではモデルの中身が理解しやすいという特徴がありましたが，ランダムフォレストではどのようにモデルが働いているかが理解しにくくなっています．

それでは具体的にどのようにscikit-learnを用いてランダムフォレストを利用するかを見ていきましょう．

scikit-learnにおけるランダムフォレストの実装

ランダムフォレストはsklearn.ensembleに実装されています．今回も変異原性の有無を予測するモデルを構築していきます．

分子の読み込み

まずはデータセットから分子を読み込みましょう．

これまでと同様に以下のコードでは

1. 必要なライブラリのインポート
2. pandasのデータフレームとして情報を読み込む
3. SMILESからRDKitのMOLオブジェクトを構築
4. 読み込めないSMILESを含むデータを除去

という順番で処理を行っています．

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem, Draw, PandasTools, Descriptors
from rdkit.Chem.Draw import IPythonConsole
print(rdBase.rdkitVersion) ## 2018.09.1
mpl.style.use('seaborn')

df = pd.read_csv('./ci900161g_si_001/smiles_cas_N6512.smi', sep='\t', header=None)
df.columns = ['smiles', 'CAS_NO', 'activity']

PandasTools.AddMoleculeColumnToFrame(frame=df, smilesCol='smiles')

df['MOL'] = df.ROMol.map(lambda x: False if x == None else True)
del_index = df[ df.MOL == False].index
df2 = df.drop(del_index)

フィンガープリントを入力ベクトルとして準備

続いて分子の情報を入力ベクトルとして変換します．今回はビット情報を分子の部分構造として可視化しようと考えていますので，フィンガープリントとしてRDKitフィンガープリントを用います．

rdkit_fp = []
for mol in df2.ROMol:
    fp = [x for x in Chem.RDKFingerprint(mol)]
    rdkit_fp.append(fp)
rdkit_fp = np.array(rdkit_fp)
rdkit_fp.shape ## (6506, 2048)

ランダムフォレストモデルの構築

ランダムフォレストで最も大切なパラメータは何個の決定木のモデルを構築するかで，n_estimatorsオプションで指定します．また各々の決定木の複雑さを制御するmax_depthなどの値も設定可能です．

ランダムフォレストの利点の1つに並列化しやすい点が挙げられます．これは多数の決定木のモデルを複数コアで別々に訓練できるためで，利用するコアの数をn_jobsオプションで指定します．-1を指定すると利用可能なコアを全て用います．

下のコードでは，1000本の決定木を作成します．モデル作成における複雑さの制限は設けませんので，訓練データにおけるランダム性（バギング）のみが重要になります．

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(rdkit_fp, df2.activity, random_state=0)
forest = RandomForestClassifier(n_estimators=1000)
forest.fit(X_train, y_train)
print('accuracy on training set: {:.3f}'.format(forest.score(X_train, y_train)))
print('accuracy on test set: {:.3f}'.format(forest.score(X_test, y_test)))

テストセットにおける精度が0.8を超えてきました．

accuracy on training set: 0.995
accuracy on test set: 0.806

ランダムフォレストモデルにおける各々の決定木モデル

構築したランダムフォレストモデルの構成要素である各々の決定木にはestimators_でアクセス可能です．

下のコードでは最初の100個の決定木における精度とランダムフォレストモデルの精度を比較することで，アンサンブル学習の効果を見てみましょう．

train_accs = []
test_accs = []
for i in forest.estimators_[:100]:
    train_accs.append(i.score(X_train, y_train))
    test_accs.append(i.score(X_test, y_test))

train_forest = forest.score(X_train, y_train)
test_forest = forest.score(X_test, y_test)
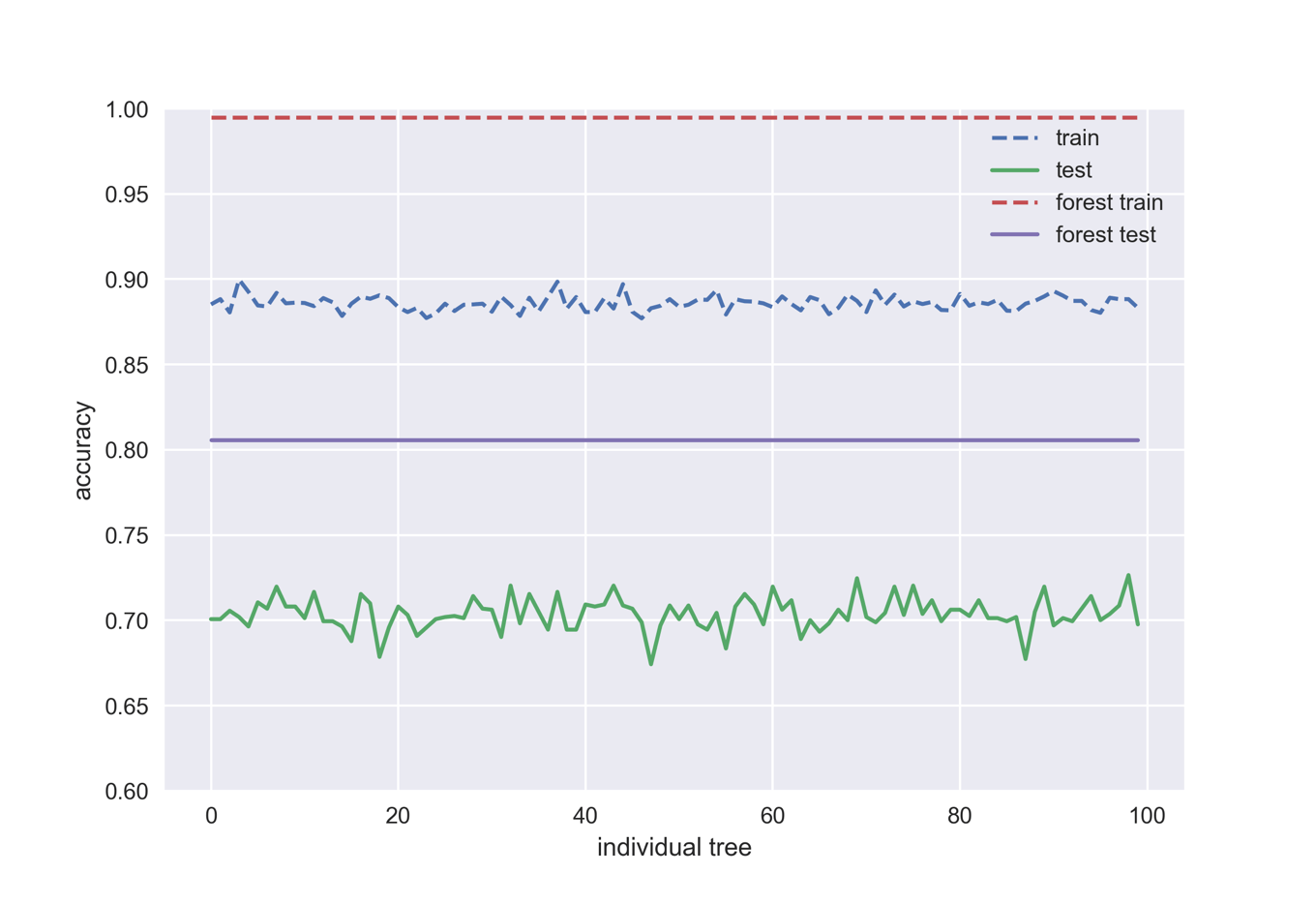
plt.plot(train_accs, '--', label='train')
plt.plot(test_accs, '-', label='test')
x = range(100)
plt.plot(x, np.ones(100)*train_forest, '--', label='forest train')
plt.plot(x, np.ones(100)*test_forest, '-', label='forest test')
plt.xlabel('individual tree')
plt.ylabel('accuracy')
plt.ylim(0.6, 1.0)
plt.legend(loc='best')

ランダムフォレストの精度は個々のモデルのどれよりも高いことが一目瞭然です．

ランダムフォレスト構築におけるパラメータの影響

続いてモデル構築段階におけるパラメータの影響を次の2点において見てみます．

• n_estimatorsを変えることによる影響
• 個々の木のmax_depthを変えることによる影響

まずはn_estimatorsを変化させてみます．

for i in [10, 100, 500, 1000, 5000]:
    f = RandomForestClassifier(n_estimators=i, n_jobs=-1)
    f.fit(X_train, y_train)
    print('--- n_estimators = {} ---'.format(i))
    print('acc on train: {:.3f}'.format(f.score(X_train, y_train)))
    print('acc on test: {:.3f}'.format(f.score(X_test, y_test)))

--- n_estimators = 10 ---
acc on train: 0.983
acc on test: 0.783
--- n_estimators = 100 ---
acc on train: 0.995
acc on test: 0.803
--- n_estimators = 500 ---
acc on train: 0.995
acc on test: 0.804
--- n_estimators = 1000 ---
acc on train: 0.995
acc on test: 0.806
--- n_estimators = 5000 ---
acc on train: 0.995
acc on test: 0.806

続いてn_estimatorsを1000に固定して，max_depthを変化させてみます．

for i in [1, 3, 5, 10, 20, 50, 100]:
    f = RandomForestClassifier(n_estimators=1000, max_depth=i, n_jobs=-1)
    f.fit(X_train, y_train)
    print('--- max_depth = {} ---'.format(i))
    print('acc on train: {:.3f}'.format(f.score(X_train, y_train)))
    print('acc on test: {:.3f}'.format(f.score(X_test, y_test)))

--- max_depth = 1 ---
acc on train: 0.653
acc on test: 0.645
--- max_depth = 3 ---
acc on train: 0.702
acc on test: 0.675
--- max_depth = 5 ---
acc on train: 0.778
acc on test: 0.730
--- max_depth = 10 ---
acc on train: 0.896
acc on test: 0.772
--- max_depth = 20 ---
acc on train: 0.970
acc on test: 0.801
--- max_depth = 50 ---
acc on train: 0.994
acc on test: 0.808
--- max_depth = 100 ---
acc on train: 0.995
acc on test: 0.804

ランダムフォレストの亜種：Extra-Trees

ランダムフォレストは非常に有用なモデルですので，さらなる改良を目指した類似モデルがたくさん存在します．ここではそのうちの１つである，Extremely Randomized Trees（ERT，Extra-Trees）について簡単に触れてみます．

通常のランダムフォレスト（決定木）では考えられるノード分割のうち評価関数を用いることで最もよい分類精度を与える特徴量を用いて分割します．一方でERTではどの特徴量で分割するかをランダムに決定します．

ERTを用いることでモデルにさらなるランダム性を導入可能になりますが，ランダムフォレストと比べて必ずしも精度が上がるわけではありません．しかし計算量の多いノード分割法を評価する部分を省略できるため，より高速にモデル構築が可能になります．

scikit-learnではERTモデルはensemble.ExtraTreesClassifierで実装されています．

from sklearn.ensemble import ExtraTreesClassifier
extree = ExtraTreesClassifier(n_estimators=1000, n_jobs=-1)
extree.fit(X_train, y_train)
print('acc on train: {:.3f}'.format(extree.score(X_train, y_train)))
print('acc on test: {:.3f}'.format(extree.score(X_test, y_test)))

acc on train: 0.995
acc on test: 0.804

モデルにおけるビットの重要度と可視化

ランダムフォレストにおける特徴量の重要度も決定木と同じくfeature_importances_で取得可能です．

plt.plot(forest.feature_importances_)
plt.xlim(0,2047)
plt.ylim(0,max(forest.feature_importances_)*1.03)
plt.xlabel('RDKit fingerprint')
plt.ylabel('feature importances')
plt.title('random forest (1000 estimators)')

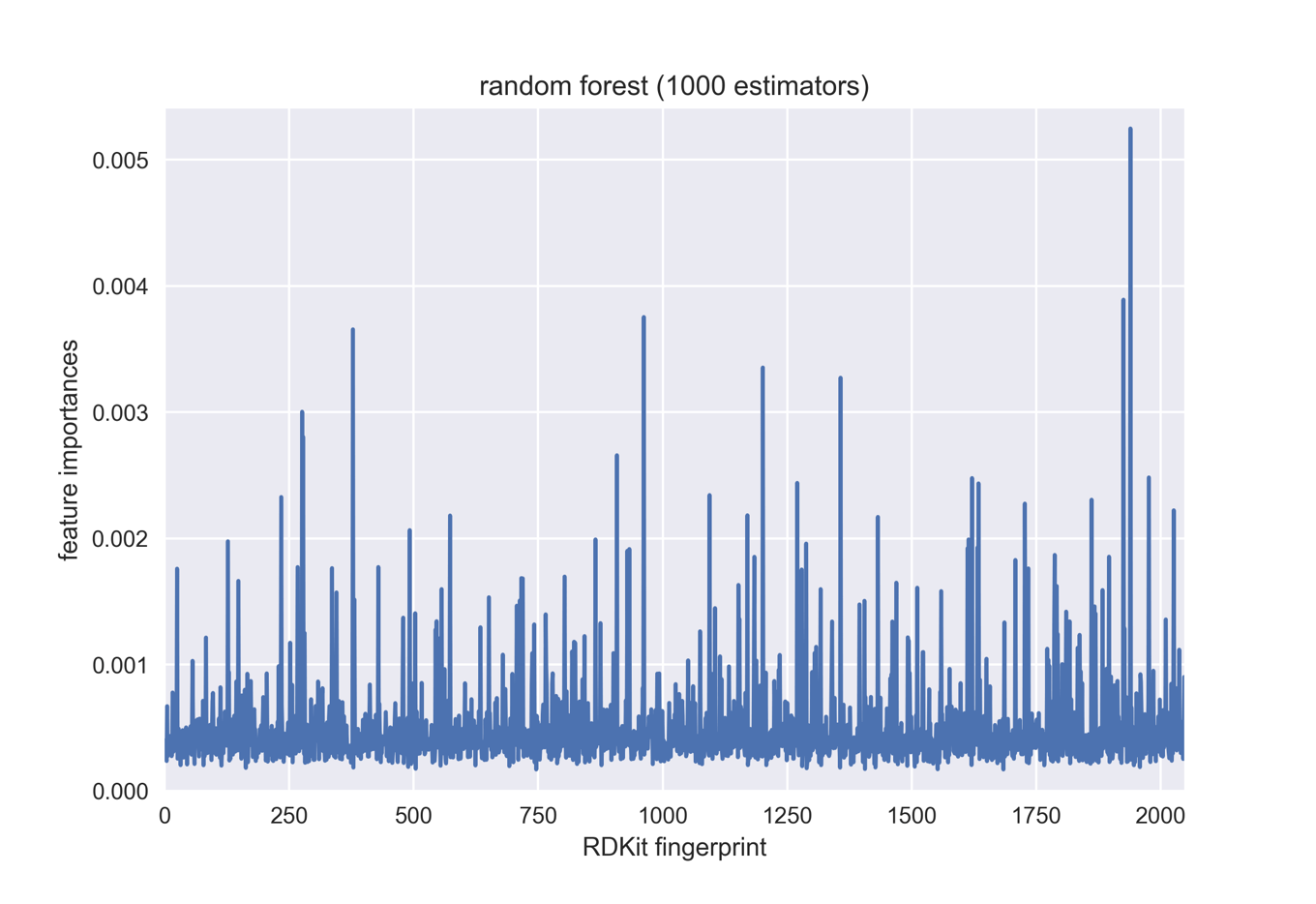
ここでは今回作成したモデルにおいて重要度の高いフィンガープリントのビット構造を可視化してみたいと思います．

以下のコードではデータセットの最初の分子に対して，

1. RDKitフィンガープリント可視化の準備
2. 作成したモデルから重要度の高い上位20の特徴量を抽出
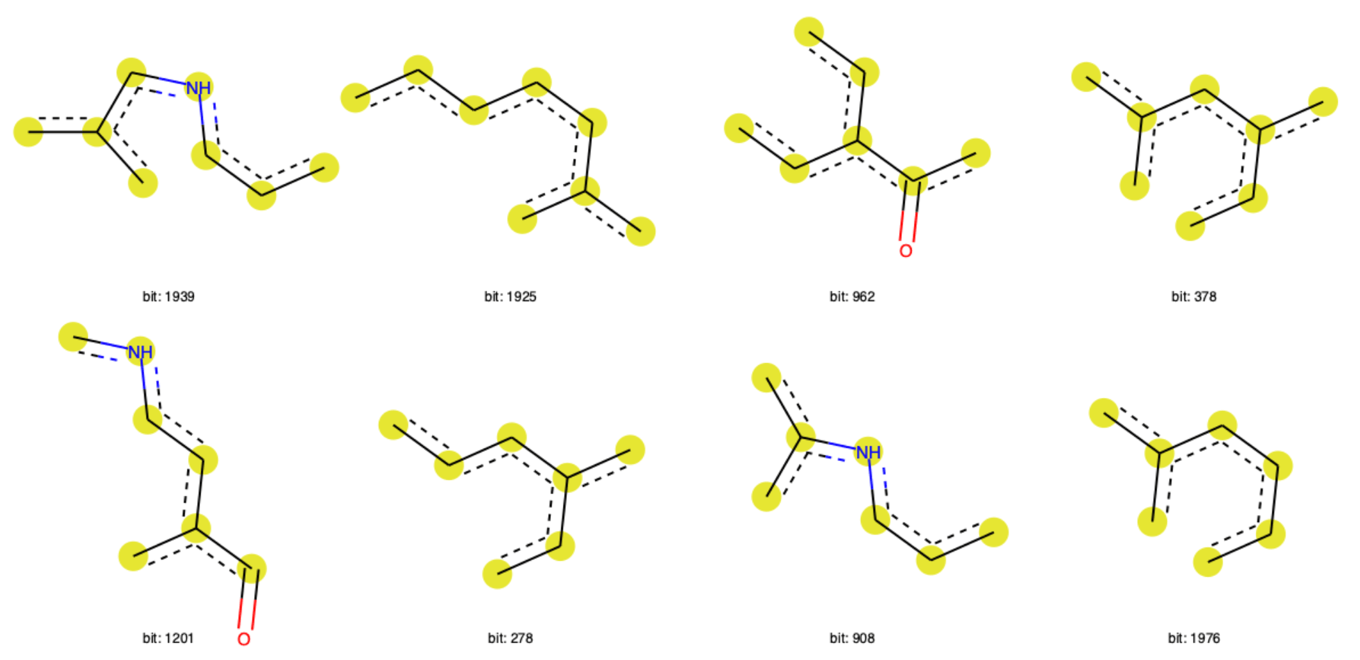
3. 上位20のうち対象分子に含まれるビットを取得（11個）
4. そのうち8個の部分構造を描画

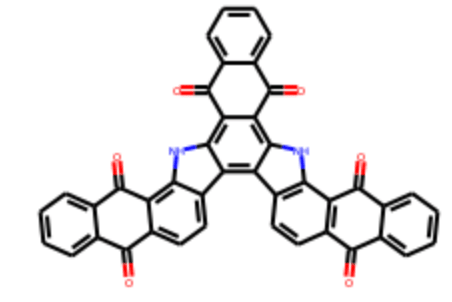
という作業を行っています．因みに最初の分子の構造は以下の通りです．

bitInfo = {}
fp = Chem.RDKFingerprint(df2.ROMol[0], bitInfo=bitInfo)

import heapq
bits = []
for i in heapq.nlargest(20, forest.feature_importances_):
    for j,k in enumerate(forest.feature_importances_):
        if j in bitInfo.keys() and i == k:
            bits.append(j)
bits ## [1939, 1925, 962, 378, 1201, 278, 908, 1976, 1861, 1727, 573]
freq_bits = []
for i in bits:
    freq_bits.append((df2.ROMol[0], i, bitInfo))
Draw.DrawRDKitBits(freq_bits[:8], molsPerRow=4, legends=['bit: '+ str(x) for x in bits[:8]])

終わりに

今回は「RDKitでランダムフォレスト：機械学習でも「みんなの意見」は案外正しい」という内容について，

• アンサンブル学習とは何か
• ランダムフォレストとは何か
• scikit-learnにおけるランダムフォレストの実装

などについて触れてきました．たくさんの弱い学習機を組み合わせることで精度を向上させることが可能であることを見ました．またモデルの重要度を用いてフィンガープリントの可視化方法について復習しました．

これまで3回にわたりAmes試験データセットを用いて，「2クラス分類」と呼ばれる教師あり機械学習問題に取り組んできました．次回は教師あり学習のもう1つの柱である「回帰」と呼ばれる問題について，「線形モデル」というアルゴリズムを用いて考えていきたいと思います．

＞＞次の記事：「線形モデルを用いた化合物の溶解度予測：通常最小二乗法，Ridge回帰，Lasso回帰」