ある化学現象に対して，分子構造から得られる性質を入力として予測モデルを組み立てることがケモインフォマティクスではよく行われます．その際に使われる分子記述子としては「分子量」などの簡単なものから，「芳香族度合」「天然物らしさ」などを表現するように化学者が工夫を凝らして作成したものまで様々であるとうことを
といった記事で説明しました．
本記事では特に少ないデータセットからより高精度の情報を取得したい場合などに使われる，量子化学計算結果を利用した記述子について取り上げます．何万件ものデータがある場合には計算コストの観点から利用できませんが，数十から数百程度なら取り入れることが可能な記述子です．
“Predictive and mechanistic multivariate linear regression models for reaction development” Chem. Sci. 2018, 9, 2398–2412.
量子化学計算と記述子
一般に過去の実験データに依存する記述子は，
- 実験データによるブレ
- 記述子によってデータがない置換基・分子が存在する
といった欠点があることから，いかなる分子においても安定して求められる計算由来の記述子は好ましいです．
特に量子化学計算の結果を利用した記述子は分子の性質を高精度に反映していると期待できることから，適切に取り入れることができれば有用になり得ます．
量子化学計算は分子力学法などと比べると計算コストが高くなりますが，例えば
- 化学反応の最適化
- in houseの同一ケモタイプにおける生理活性予測
といった，データ数が数十から数百程度の場合には利用を考えてもいいでしょう．
その際には，このような記述子では分子全体よりも置換基や特定原子に着目したものが多く，データセット中の分子構造をうまく作成しないと自動化によって必要な記述子を取得することが困難になり手作業が増える恐れがあることは念頭に置いておく必要があります．
置換基・分子の立体因子に関する記述子
立体因子は化学反応における基質–基質や基質–触媒相互作用において重要な役割を担うことから，「立体因子」を定量的に表現可能な記述子が開発されてきました．
これらは大きく分けて，
- 置換基の立体因子を表現する記述子
- 触媒中の配位子の立体因子を表現する記述子
とに分類できます．
Taft–Chartonパラメータ（立体置換基定数）
脂肪族メチルエステルの酸加水分解速度をもとに算出した立体因子の記述子をTaft値といいます．このオリジナルの実験値をもとに，Chartonがvan der Waals半径をもとに改良したものがTaft–Chartonパラメータになります．
Taft–Chartonパラメータは反応速度をもとに算出していますので，置換基の様々なコンフォメーションによる効果を１つの代表値として表現していると考えられます．
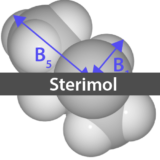
Sterimolパラメータ
Sterimolパラメータは1970年代にVerloopらが考案した一連のパラメータです．Taft–Chartonパラメータでは立体因子を1つの値で表していましたが，SterimolパラメータではB1, B5, Lという3つの値で表現するため，より柔軟に立体因子を表現可能になっています．
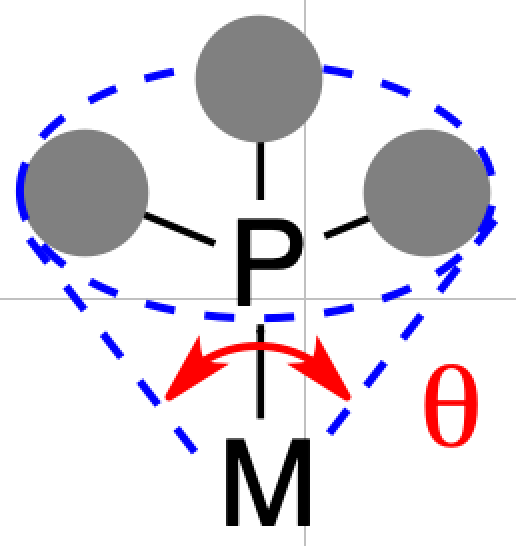
リン配位子の円錐角
Tolmanはリン配位子の嵩高さを記述するために円錐角（cone angle）と呼ばれる概念を導入しました．
円錐角は下記のように金属を頂点としたリン上置換基に外接する円錐を考えた際の円錐角です．置換基が嵩高くなるほど円錐角は大きくなります．なお文献で知られている値はニッケルを中心金属としてNi–P結合を2.28 Åに固定した値になります．
N-へテロ環状カルベン（NHC）配位子の立体因子：%VBur
Tolmanの円錐角の報告以降，遷移金属化学ではBuchwaldのビアリール型配位子やN-へテロ環状カルベン（NHC）配位子など，円錐角で立体因子を記述するのが困難な配位子が多く開発されました．
Nolanらは特にNHC配位子の立体因子を記述するために，下図のような金属を中心とした球において配位子が占める体積の比率（Buried volume; %VBur）を定義しました．
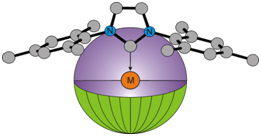＜SambVca 2.1ヘルプページより転載＞
X線構造や計算構造を基にした%VBurはCavalloらが開発したオンラインツール「SambVca 2.1」にて算出可能です．
“SambVca: A Web Application for the Calculation of the Buried Volume of N‐Heterocyclic Carbene Ligands” Eur. J. Inorg. Chem. 2009, 1759.
・SambVca 2.1の元文献
“Towards the online computer-aided design of catalytic pockets” Nature Chem. 2019, 11, 872.
構造の歪み角度
例えば遷移金属錯体中における二座型配位子の配位角は還元的脱離の速度に影響するなど，「角度」は化合物の性質や反応性を大きく規定します．
アラインの反応位置については立体障害，電荷密度，フロンティア軌道などによる説明がされていましたが，これらの要因から予測される位置とは異なる点で反応する例が多数知られていました．
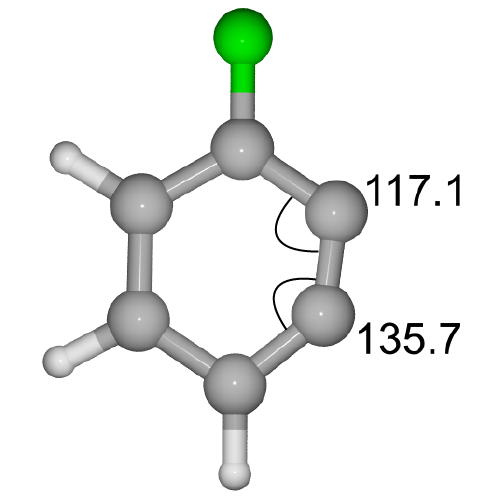
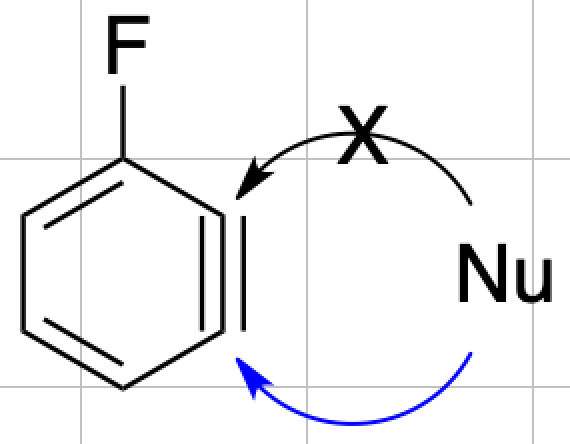
UCLAのGarg，Houkらのグループは一連のアライン・ヘテラインの研究において，化合物の歪みが三重結合の反応位置予測に有用であることを示しました．例えば下記のフッ素置換アラインでは1位炭素の方がより歪んでいるため反応性が高いと予測されました．この予測は実際に実験的に確かめられました．
置換基・分子の電子的効果に関する記述子
Hammettの置換基定数は
- 安息香酸誘導体の酸解離定数（pKa）という熱力学的現象
- 安息香酸エステルの塩基加水分解速度という速度論的現象
を代表例として直線自由エネルギー関係を示すと導入されました．
その後もHammettの置換基定数は様々な反応において線形性を示すことが示され，芳香環上のパラ位およびメタ位置換基の電子効果を表現する方法として物理有機化学の分野で有用性が広く実証されています．
このような背景から電子的効果を見積もる記述子としては，
- 量子化学計算で容易に算出可能
- Hammettパラメータと相関がある
という2つの条件を満たすものが人気があるようです．
最も下記に示す記述子は必ずしも電子的効果のみを表現するのではなく，立体因子との複合的効果を記述していると考えられます．また相互に相関が強いことから，実際の運用においては相関係数をきちんと眺めた上で，記述子の取捨選択を行う必要があるでしょう．
IRの振動数と強度
化合物のIRに関する情報は原子座標の二階微分から調和振動子近似のもとで得られます．多くの量子化学計算プログラムが解析的方法を提供していることから，やや計算コストは高いですが容易に得られる情報の１つです．
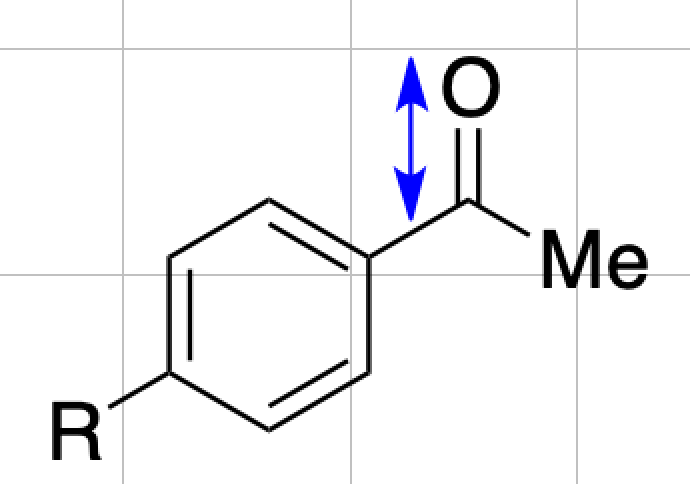
またパラ位置換アセトフェノン誘導体のカルボニル振動数とHammett定数がよい相関を示すことが知られていることから，計算可能なHammett定数の代替品と考えることができます．
分子の電荷密度（atomic charge）
多くの量子化学計算プログラムではエネルギー計算とともに，双極子モーメントや電荷密度解析も行われます．特に分子内の原子にどのように電荷が配分されているかという情報は反応性の理解に重要であり，記述子として使われています．
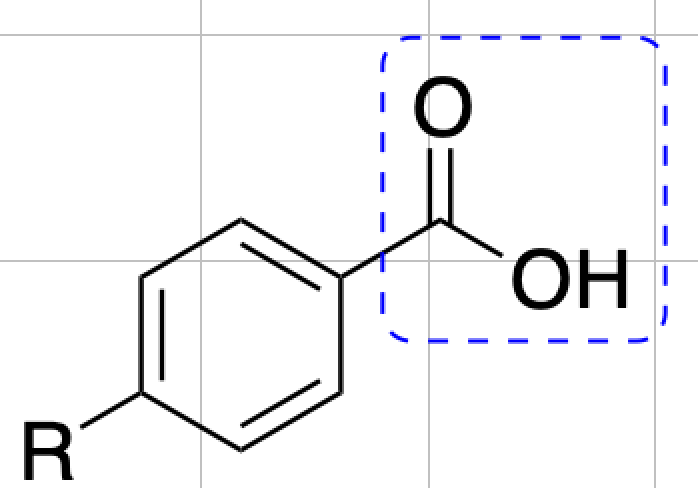
この目的ではMuliken電荷は基底関数系による不安定性があることから，NBO解析の枠組み内のNPA電荷が使われています．例えば安息香酸誘導体のカルボキシル基のNPA電荷と酸解離定数との間に良い相関があることが報告されています．
NMRのケミカルシフト
NMRケミカルシフトは分子中の各原子の電子的・立体的環境を反映しており，量子化学計算によって計算可能であることから記述子として利用可能です．特に範囲の広い炭素やリンなどがよく利用されます．
終わりに
今回は「量子化学計算を利用した記述子：統計モデルにおける立体因子と電子的効果」という話題について，
- 立体因子
- 電子的効果
にわけて，量子化学計算によって算出可能な記述子をいくつか説明してきました．冒頭でも述べたように，
- 計算コストがやや高い
- データセットの性質によっては手作業が増える
といった理由から大きなデータセットには不向きな手法ではありますが，覚えておくとよいと思います．
コメント