本ブログではPythonのオープンソースライブラリであるPsi4を用いて,量子化学計算の初心者を対象にした記事を多数用意しています。
記事の内容を一つずつ習得することで,これから計算化学を始めたい人が知識・経験ゼロの状態から徐々にステップアップしていくことで,量子化学計算の基本コンセプトが習得できるように構成されています。
Psi4のインストールから最初の量子化学計算まで
「計算化学にpythonとPsi4で入門」という記事では,
- Psi4とは何か
- Psi4のインストール方法
- 水分子のエネルギー計算を題材としたインプットファイルの作成法
などを解説しています。
Google Colab上でのPsi4の環境構築方法
初心者の方ですと,そもそも自分のコンピュータ上にPsi4の実行環境を用意することが困難な場合もあると思います。
「Google ColabでPsi4:量子化学計算用のpython環境を手軽に構築」という記事では,Psi4を自分のコンピュータにインストールすることが難しい方のために,Google Colab上での環境構築方法について解説しています。
これでiPadなどのタブレット端末からも量子化学計算を実行することが可能になります。

Psi4を用いた構造最適化計算
構造最適化計算とは,分子構造を少しずつ変化させながらエネルギー計算を繰り返すことでエネルギー極小値を与える構造を求める方法です。分子の安定構造が求められるために,興味のある分子に対してまず実施する計算になります。
「計算化学の構造最適化の基本をPsi4で学ぶ」では,Psi4を用いた構造最適化計算について説明しています。

Psi4で困難な構造最適化に対応する
構造最適化は興味のある分子に対して行う最初の計算であるにも関わらず,エラーに悩まされることも少なくありません。Psi4では構造最適化が難しい分子系に対応するためにGeomeTRICと呼ばれる外部プログラムと連携することが可能です。
「Psi4の構造最適化でGeomeTRICを使う」という記事では,
- GeomeTRICとは何か
- Psi4からGeomeTRICを使う方法
- Optkingにおける制約付き最適化の復習
- GeomeTRICを用いた制約付き最適化の方法
について具体例を用いて説明しています。

Psi4を用いた振動数計算
構造最適化計算では予め定めた終了判定基準を満たす構造に収束させます。得られた構造が安定構造か,不安定構造かを調べるのが振動数計算と呼ばれる計算方法です。
「Psi4における振動数計算:IRスペクトルや異性体間のエネルギー差を計算」という記事では,
- 振動数計算の実行方法
- 計算振動数とIR振動数を比較する際の注意点
- 計算により得られるエンタルピーやエントロピーなど熱化学諸量の使い方
などの項目について具体例を用いてやさしく解説しています。
Psi4を用いた遷移状態の最適化
化学反応において,原系と生成系を結ぶ反応座標上の極大値を遷移状態と呼びます。遷移状態がわかれば反応の活性化エネルギーを見積もったり,反応機構の解析などが行えます。実験的には直接観測できない遷移状態の構造を見ることができるのは,計算化学のメリットの1つです。
「Psi4で遷移状態最適化:計算化学における虚振動と化学構造」という記事では,化学反応の遷移状態を計算する方法について基本から説明しています。
Psi4で反応経路の計算
遷移状態とは原系と生成系を結ぶ構造です。計算化学において遷移状態が繋ぐ構造を確認するには,最小エネルギー経路(Minimum Energy Path)を求める必要があります。固有反応座標(IRC: Intrinsic Reaction Coordinate)は質量加重座標における最小エネルギー経路です。
「Psi4でIRC計算:固有反応座標で反応経路を求める」という記事では,Psi4を用いたIRC計算のやり方を基本から説明しています。原系から遷移状態を経て生成系へと繋がる反応経路の計算方法について説明しています。
Psi4で分子軌道の可視化
シュレディンガー方程式を解くことで得られる分子軌道は分子周辺に3次元的に広がっています。そのため計算化学では,分子軌道のような3次元空間に広がる値を記録する共通のフォーマット形式が利用されています。
「Psi4とCubeファイル:分子軌道や静電ポテンシャルマップの可視化」という記事では,
- Cubeファイルとは何か
- Psi4でのCubeファイル作成方法
- Cubeファイルを用いた可視化方法
について分子軌道や静電ポテンシャルマップを例に説明しています。

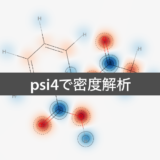
Psi4で電子密度解析
シュレディンガー方程式を解くことで得られる波動関数からは,さまざまな情報が得られます。これら情報はPsi4ではWavefunctionオブジェクトに格納されています。
「計算化学における電荷:Psi4を用いた電子密度解析」という記事では,Psi4のWavefunctionオブジェクトの使い方について説明しています。特に
- 電子密度解析
- 双極子モーメント
- 結合次数
について具体例を通して学んでいきます。
Psi4を用いた基底関数重なり誤差の計算方法
化学現象は分子同士の相互作用によって生じます。そのため相互作用エネルギーの算出は重要です。計算化学では相互作用エネルギーは超分子法と呼ばれる方法で計算されます。
「Psi4で分子間相互作用エネルギーの計算:超分子法と基底関数重なり誤差」という記事では,
- 超分子法とその注意点について
- Psi4で超分子法を用いて相互作用エネルギーを計算する方法
について説明しています。

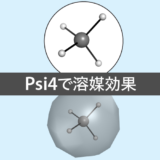
Psi4で溶媒効果を取り込む方法
量子化学計算の多くは真空中での孤立分子を対象に行われます。このような限定的な条件でも,量子化学計算は分子構造やエネルギーに関し,有用な示唆を与えてくれます。
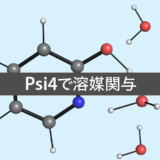
しかし多くの化学反応は液相中で行われることから,溶媒効果を計算結果に取り込むことができれば,より有用な知見が得られます。
という記事では,Psi4を用いて溶媒効果を取り込む方法について基本的な事項から説明しています。
計算レベルとエネルギー計算の注意点
量子化学計算はシュレディンガー方程式やコーン・シャム方程式を近似的に解く試みです。そのためどのような近似を行うかによって,得られる値が変わってきます。計算手法によっては考慮できない相互作用なども存在します。
「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事ではPsi4を用いてエネルギー計算を行いながら,計算手法とエネルギーの関係を説明しています。
Psi4で3cコンポジット法を使う
Psi4では,精度を犠牲にせず・より計算コストの低い密度汎関数法を目指して開発されている3cコンポジット法が実装されています。
「Psi4で3cコンポジット法を利用する」という記事では,
- 3cコンポジット法とは何か
- 3cコンポジット法の性質・特徴
- Psi4で利用可能な3cコンポジット法
について説明しています。
Psi4に実装されていない基底関数系を使う
分子軌道法やDFTでは分子軌道を基底関数の線形結合として表現し,分子軌道の関数系に制限を加えます。基底関数の集まりを基底関数系といいます。
基底関数系は量子化学計算の精度を決める大切な要素であり,さまざまなものが報告されています。Psi4でも数多くの基底関数系が実装されています。しかし,全ての基底関数系がサポートされているわけではありません。Basis Set Exchange(BSE)は今まで報告された基底関数系を集めたデータベースです。
「Basis Set Exchangeは基底関数系に関するデータベース:pythonとPsi4を用いてECPを自在に扱う」という記事では,
- BSEの説明とPythonを用いた使い方
- Psi4を用いた基底関数系の設定方法
について説明しています。


