これまで本ブログでは量子化学計算用のpythonライブラリであるPsi4について,「計算化学にPythonとPsi4で入門」や「計算化学の構造最適化の基本をPsi4で学ぶ」という記事を通じて
- 計算のセットアップ方法
- エネルギー計算
- 構造最適化計算
をはじめとする基本的な使い方を説明してきました.今回は「振動数計算」と呼ばれる計算手法について説明していきます.
振動数計算は化合物のIRスペクトル予測に利用可能である他,最適化構造が極小値(安定構造)であるか極大値(遷移状態)であるかを調べるのにも必要な重要な計算です.さらに得られた振動数データから,ゼロ点エネルギーやエンタルピー,エントロピーのエネルギー補正値も算出可能であるため,異性体間の安定性や化学反応を議論する際にも必須となります.

Psi4における振動数計算
今回の計算は以下の環境で,コマンドラインより.pyファイルを実行しています.下記でも述べていますが,振動数計算は計算コストの高い計算手法ですので,手元の環境で動かす場合は適宜計算レベルを落とすなどの調整をしてみてください.
import sys
import numpy as np
import pandas as pd
import matplotlib as mpl
import psi4
print(f'python version:\n{sys.version}')
print(f'numpy version: {np.__version__}')
print(f'pandas version: {pd.__version__}')
print(f'matplotlib version: {mpl.__version__}')
print(f'psi4 version: {psi4.__version__}')
# python version:
# 3.9.7 (default, Sep 16 2021, 13:09:58)
# [GCC 7.5.0]
# numpy version: 1.21.4
# pandas version: 1.3.4
# matplotlib version: 3.4.3
# psi4 version: 1.4.1
振動数計算の実行
振動数計算はpsi4.frequencyで実行します.freqやfrequenciesでも同じ計算を実行します.
注意点として振動数は「構造依存的」であるため,最適化構造にて振動数計算を実施する必要があります.非最適化構造についても振動数計算は実行可能ですが,得られる結果に意味はありません.Gaussian/GaussViewなどでは「構造最適化+振動数」を一緒に行う「opt + freq」オプションが用意されているのも,この2つの計算を同時に行う需要が極めて大きいためです.
psi4では構造最適化後にはMoleculeオブジェクトの原子座標が自動更新されます.そのため以下のように同じ分子を対象に,構造最適化と同じ計算レベルで続けて実施することで実行可能です.ref_gradientオプションにて構造最適化で得られたWavefunctionオブジェクトを指定することで,振動数計算におけるgradient計算を省くことが可能です.
以下のコードでは同じトルエンの初期座標に対して,
- B3LYP/6-31G(d)レベルで構造最適化
- 最適化構造に対して同レベルにて振動数計算
を行っています.ref_gradientオプションの有無で計算速度に違いが出ていることがわかります.
import time
import pathlib
import numpy as np
import psi4
file_name = pathlib.Path(__file__)
logfile = file_name.with_suffix('.log').name
# 計算環境の設定
psi4.set_output_file(logfile)
psi4.set_memory('14GB')
psi4.set_num_threads(20)
# トルエンの初期構造
toluene = psi4.geometry('''
0 1
C -1.53273800 -1.17063490 0.00000000
C -0.13757800 -1.17063490 0.00000000
C 0.55996000 0.03711610 0.00000000
C -0.13769400 1.24562510 -0.00119900
C -1.53251900 1.24554710 -0.00167800
C -2.23012000 0.03734110 -0.00068200
H -2.08249700 -2.12295190 0.00045000
H 0.41193000 -2.12314790 0.00131500
H 0.41250600 2.19776810 -0.00125800
H -2.08264100 2.19782810 -0.00263100
H -3.32972400 0.03752410 -0.00086200
C 2.09995974 0.03722813 0.00088786
H 2.45720669 0.04964567 -1.00763602
H 2.45626596 0.90464367 0.51618986
H 2.45640595 -0.84252715 0.49472665
''')
# 構造最適化
print('## start opt')
start = time.time()
e, wfn = psi4.optimize('b3lyp/6-31G(d)', molecule=toluene, return_wfn=True)
end = time.time()
print(f'It took {end - start:.3f} sec for the optimization.')
# 振動数計算
print('## start freq')
start = time.time()
e, wfn = psi4.frequency('b3lyp/6-31g(d)', molecule=toluene, ref_gradient=wfn.gradient(), return_wfn=True)
end = time.time()
print(f'It took {end -start:.3f} sec for the freq computation.')
print(f'Frequencies:\n{np.array(wfn.frequencies())}')
timeコマンドで計測した実行時間は以下の通りです.
| ref_gradientなし | ref_gradientあり | |
|---|---|---|
| real | 9m24.943s | 9m17.962s |
| user | 157m6.128s | 154m37.419s |
| sys | 12m53.646s | sys 12m35.456s |
pythonスクリプト中でtime.time()を用いて計測した時間は以下の通りでした.最適化計算ではなく,振動数計算の時間が短くなっていることが見て取れます.また構造最適化と比べて振動数計算は何倍もの時間がかかることがわかります.このため高レベルの振動数計算を実行することは,分子の大きさや数によっては現実的でないこともあります.
| ref_gradientなし | ref_gradientあり | |
|---|---|---|
| opt | 28.256 | 28.558 |
| freq | 535.606 | 528.327 |
計算された振動数の取り出し
Wavefunction.hessian()
計算された振動数はログファイルに書き込まれるだけでなく,Wavefunctionオブジェクトからも取得可能です.上記のスクリプトではnumpy配列として受け取っています.また振動数計算は2階偏微分に相当しますので,ヘッセ行列(Hessian)も計算過程で得られており,こちらも取り出すことが可能です.
出力は下記のようになりました.なお虚振動が存在する場合は負の値として出力されます.
Frequencies: [ 29.69822334 210.72813372 342.50049345 417.40651922 477.60164812 528.31633969 637.46717647 711.54611652 747.69443601 801.47673931 860.35810514 910.55748333 964.30968306 992.16469264 1012.78883702 1018.25154547 1059.70126928 1076.14007414 1122.01334589 1191.97146577 1214.73412232 1239.06402806 1349.16232022 1367.57348455 1442.78349818 1490.82049097 1518.54648464 1528.80199457 1548.77072945 1645.28590111 1667.70880046 3039.52948357 3096.30962049 3122.90713383 3171.40770547 3173.09263669 3185.604889 3193.93745995 3206.62338359]
振動数計算のレベルとスケールファクター
前述のように振動数計算はコストの高い計算ですので,闇雲に高精度で実行することはできません.以下ではエタンの構造最適化と振動数計算をいくつかの計算レベルで行い,得られる振動数の違いについて見ていきましょう.具体的には
- HF/3-21G
- MP2/6-31G(d)
- MP2/6-31+G(d,p)
- B3LYP/6-31G(d)
- B3LYP/6-31+G(d,p)
- MP2/6-311++G(2d,p)
の6つの計算レベルにて計算を行い,得られる振動数をpandasデータフレームとしています.
coord = '''
0 1
C -0.70932535 0.17857143 0.00000000
H -0.35267093 -0.83023858 0.00000000
H -0.35265251 0.68296962 -0.87365150
H -1.77932535 0.17858461 0.00000000
C -0.19598313 0.90452770 1.25740497
H -0.55103948 1.91390079 1.25642745
H -0.55425224 0.40125927 2.13105486
H 0.87401506 0.90282101 1.25838372
'''
levels = ['hf/3-21g', 'mp2/6-31g(d)', 'mp2/6-31+g(d,p)', 'b3lyp/6-31g(d)', 'b3lyp/6-31+g(d,p)', 'mp2/6-311++g(2d,p)']
ethane_results = pd.DataFrame()
for level in levels:
ethane = psi4.geometry(coord)
start = time.time()
_, wfn = psi4.optimize(level, molecule=ethane, return_wfn=True)
_, wfn = psi4.frequency(level, molecule=ethane,
ref_gradient=wfn.gradient(),
return_wfn=True)
end = time.time()
print(f'It took {end - start:.2f} sec at the {level} level of theory.')
ethane_results[level] = np.array(wfn.frequencies())
ethane_results.to_csv('ethane_results.csv')
様々なレベルで得られた振動数の,MP2/6-311++G(2d,p)レベルで得られた振動数に対する比を求めたものが以下になります.振動数は全部で18個です.
| hf/3-21g | mp2/6-31g(d) | mp2/6-31+g(d,p) | b3lyp/6-31g(d) | b3lyp/6-31+g(d,p) | mp2/6-311++g(2d,p) | |
|---|---|---|---|---|---|---|
| count | 18.00 | 18.00 | 18.00 | 18.00 | 18.00 | 18.00 |
| mean | 1.06 | 1.02 | 1.02 | 1.00 | 0.98 | 1.0 |
| std | 0.04 | 0.01 | 0.01 | 0.01 | 0.00 | 0.0 |
| min | 0.98 | 1.01 | 1.01 | 0.98 | 0.98 | 1.0 |
| 25% | 1.03 | 1.01 | 1.01 | 0.99 | 0.98 | 1.0 |
| 50% | 1.09 | 1.02 | 1.02 | 1.00 | 0.98 | 1.0 |
| 75% | 1.10 | 1.03 | 1.02 | 1.00 | 0.99 | 1.0 |
| max | 1.11 | 1.04 | 1.05 | 1.01 | 0.99 | 1.0 |
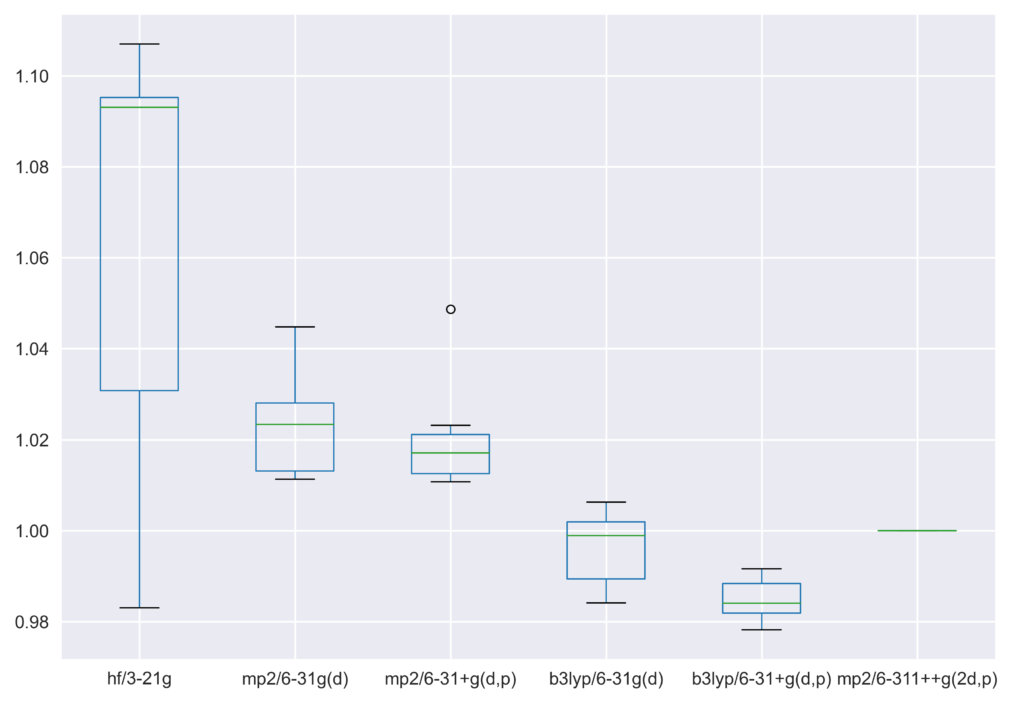
箱ヒゲ図から,HF/3-21Gを除き一貫した比率で振動数値がずれていることが見て取れます.HF法では電子相関が考慮されないため,共有結合を過大評価し大きめの値が算出されることがわかっています.
このように,ある計算レベルで求めた振動数とIRの実験値では系統的なズレがあることが古くより知られていました.そこで低精度の計算値に対して,ある係数を乗ずることで実験値を再現する試みが行われており,データベース化されています.
異性体間のエネルギー比較
調和振動子近似により,各振動モードからゼロ点エネルギーや熱振動エネルギー,振動エントロピーが計算可能です.これら計算は容易に実行可能なので,通常の計算ソフトでは振動数計算を行う際には,並進,回転エネルギーと併せて
- ゼロ点エネルギー
- 内部エネルギー
- エンタルピー
- エントロピー
の値も計算されます.
今回は「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事でも題材とした, 1,2-ジフルオロエタンについて異性体エネルギー差を計算してみます.この分子は実験・理論の両面からよく研究されており,gauche型配座の方が安定であることがわかっています.
以前の記事では様々な計算レベルでgauche型とanti型の最適化計算を行い,得られた電子エネルギーの差を比較しました.今回はさらに振動数計算も行うことでより正確な評価をしていきます.具体的には
- HF, B3LYP, B3LYP-D3(BJ), wB97X-D
- 3-21G, 6-31G(d)
の各々の組み合わせ全8通りについて計算を行っています.もしも振動数のリストに虚振動が含まれる場合は構造最適化が失敗していますので,アラートを出力するようにしています(幸い,今回は全ての場合で最適化が成功しています).
from __future__ import annotations
import sys
import time
import pathlib
import itertools
import numpy as np
import pandas as pd
import psi4
file_name: pathlib.Path = pathlib.Path(__file__)
logfile: str = file_name.with_suffix('.log').name
psi4.set_output_file(logfile)
psi4.set_memory('14GB')
psi4.set_num_threads(12)
print(f'python version:\n{sys.version}')
print(f'numpy version: {np.__version__}')
print(f'psi4 version: {psi4.__version__}')
gauche: str = '''
0 1
C -1.19543643 -0.19841270 0.00000000
H -0.83878201 -1.20722270 0.00000000
H -0.83876359 0.30598549 -0.87365150
C -0.68209421 0.52754358 1.25740497
H -1.04036332 0.02427515 2.13105486
H 0.38790398 0.52583689 1.25838372
F -2.54543643 -0.19839606 0.00000000
F -1.13006250 1.80105168 1.25617165
'''
anti: str = '''
0 1
C -1.19543643 -0.19841270 0.00000000
H -0.83878201 -1.20722270 0.00000000
H -0.83876359 0.30598549 -0.87365150
C -0.68209421 0.52754358 1.25740497
H -1.03874884 1.53635351 1.25740509
H -1.03876691 0.02314493 2.13105626
F -2.54543643 -0.19839606 0.00000000
F 0.66790579 0.52752676 1.25740465
'''
theories: list[str] = ['hf', 'b3lyp', 'b3lyp-d3bj', 'wb97x-d']
basis_sets: list[str] = ['3-21g', '6-31g(d)']
confs: list[str] = [gauche, anti]
gauche_energies = []
gauche_frequencies = []
anti_energies = []
anti_frequencies = []
def optimize_mol(coord: str, level: str)\
-> tuple[psi4.core.Molecule, psi4.core.Wavefunction]:
molecule: psi4.core.Molecule = psi4.geometry(coord)
_, wfn = psi4.optimize(level,
molecule=molecule,
return_wfn=True)
return (molecule, wfn)
def freq_mol(level: str, molecule: psi4.core.Molecule,
wfn: psi4.core.Wavefunction)\
-> tuple[float, np.ndarray]:
energy, wfn = psi4.frequency(level,
molecule=molecule,
ref_gradient=wfn.gradient(),
return_wfn=True)
frequencies = np.array(wfn.frequencies())
print(f'\nFrequencies:\n{frequencies}\n')
return (energy, frequencies)
def check_img(frequencies: np.ndarray) -> bool:
if np.sum(frequencies < 0) == 0:
return True
else:
return False
for theory, basis in itertools.product(theories, basis_sets):
level: str = theory + '/' + basis
for conf in confs:
print(f'## start optimization at the {level} level of theory. ##')
start = time.time()
mol, wfn = optimize_mol(conf, level)
end = time.time()
print(f'It took {end - start:.3f} secs for the opt computation.\n')
print(f'## start freq calculation at the {level} level of theory. ##')
start: float = time.time()
energy, freqs = freq_mol(level, mol, wfn)
end = time.time()
print(f'It took {end - start:.3f} secs for the freq computation.\n')
if not check_img(freqs):
print('##################################')
print('##### OPTIMIZATION FAILED !! #####')
print('##################################')
break
if conf == gauche:
gauche_energies.append(energy)
gauche_frequencies.append(freqs)
if theory == 'wb97x-d':
with open('wb97xd_gauche.dat', 'w') as f:
f.write(mol.save_string_xyz())
else:
anti_energies.append(energy)
anti_frequencies.append(freqs)
if theory == 'wb97x-d':
with open('wb97xd_anti.dat', 'w') as f:
f.write(mol.save_string_xyz())
calc_results = pd.DataFrame({'gauche_energy': gauche_energies,
'anti_energy': anti_energies})
calc_results['diff'] = psi4.constants.hartree2kcalmol * (calc_results['gauche_energy'] - calc_results['anti_energy'])
calc_results.index = [theory + '/' + basis for theory, basis in itertools.product(theories, basis_sets)]
calc_results.to_csv('calc_results.csv')
HF/3-21Gでのゼロ点エネルギーなどの値はログファイル中では以下のように出力されています.
==> Thermochemistry Energy Analysis <==
Raw electronic energy, E0
Total E0, Electronic energy at well bottom at 0 [K] -78.79394038 [Eh]
Zero-point energy, ZPE_vib = Sum_i nu_i / 2
Electronic ZPE 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Translational ZPE 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Rotational ZPE 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Vibrational ZPE 50.231 [kcal/mol] 210.168 [kJ/mol] 0.08004891 [Eh] 17568.705 [cm^-1]
Correction ZPE 50.231 [kcal/mol] 210.168 [kJ/mol] 0.08004891 [Eh] 17568.705 [cm^-1]
Total ZPE, Electronic energy at 0 [K] -78.71389147 [Eh]
Thermal Energy, E (includes ZPE)
Electronic E 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Translational E 0.889 [kcal/mol] 3.718 [kJ/mol] 0.00141628 [Eh]
Rotational E 0.889 [kcal/mol] 3.718 [kJ/mol] 0.00141628 [Eh]
Vibrational E 50.591 [kcal/mol] 211.675 [kJ/mol] 0.08062257 [Eh]
Correction E 52.369 [kcal/mol] 219.111 [kJ/mol] 0.08345512 [Eh]
Total E, Electronic energy at 298.15 [K] -78.71048526 [Eh]
Enthalpy, H_trans = E_trans + k_B * T
Electronic H 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Translational H 1.481 [kcal/mol] 6.197 [kJ/mol] 0.00236046 [Eh]
Rotational H 0.889 [kcal/mol] 3.718 [kJ/mol] 0.00141628 [Eh]
Vibrational H 50.591 [kcal/mol] 211.675 [kJ/mol] 0.08062257 [Eh]
Correction H 52.961 [kcal/mol] 221.590 [kJ/mol] 0.08439931 [Eh]
Total H, Enthalpy at 298.15 [K] -78.70954107 [Eh]
Gibbs free energy, G = H - T * S
Electronic G 0.000 [kcal/mol] 0.000 [kJ/mol] 0.00000000 [Eh]
Translational G -9.292 [kcal/mol] -38.878 [kJ/mol] -0.01480789 [Eh]
Rotational G -5.028 [kcal/mol] -21.038 [kJ/mol] -0.00801284 [Eh]
Vibrational G 50.063 [kcal/mol] 209.462 [kJ/mol] 0.07977974 [Eh]
Correction G 35.742 [kcal/mol] 149.546 [kJ/mol] 0.05695901 [Eh]
Total G, Free enthalpy at 298.15 [K] -78.73698137 [Eh]
「Total H,」や「Total G,」でログファイルの検索をかければ,それぞれエンタルピー,自由エネルギーの計算値が,「Correction H」や「Correction G」で各々の補正項の取得が可能です.
ログファイルより抽出した結果をもとに,各計算レベルで結果をkcal/mol単位でまとめたものが以下の表になります.高精度になるほど,gauche体の安定性をきちんと評価できていそうです.
| level | H (kcal/mol) | G (kcal/mol) |
|---|---|---|
| HF/3-21G | 0.7522 | 0.8847 |
| HF/6-31G(d) | 0.3795 | 0.4518 |
| B3LYP/3-21G | -0.3099 | -0.0755 |
| B3LYP/6-31G(d) | -0.4916 | -0.3762 |
| B3LYP-D3(BJ)/3-21G | -0.3165 | -0.0830 |
| B3LYP-D3(BJ)/6-31G(d) | -0.5030 | -0.3878 |
| wB97X-D/3-21G | -0.1425 | 0.0283 |
| wB97X-D/6-31G(d) | -0.4396 | -0.3912 |
エネルギー計算と構造最適化・振動数計算を異なる計算レベルで行う
振動数計算を高精度で行うことは計算コストの観点から現実的でない場合が多々あります.そういった際に使われている手法として,「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事でも紹介した「エネルギー計算と構造最適化・振動数計算を異なる計算レベルで行う」ことがなされています.
例えば下の囲みで示す
のように「//」で区切られた表記方法は,
- 計算レベル2で最適化・振動数計算
- 計算レベル2で最適化した構造に対して,計算レベル1でエネルギー計算
という2段階でエネルギーを評価する計算手法を意味しています.ある程度の大きさの有機化合物を対象とした計算化学の論文でよく見る表記方法です.
この場合,自由エネルギーなどの算出には,計算レベル2の振動数計算で得られた補正項を計算レベル1で得たエネルギーに加えることで対応しています.
もちろん計算レベル1と計算レベル2では最適化構造は異なるため,このような補正は厳密には正しくありませんが,前述のように振動数は計算手法を変えてもあまり変化しない(系統的に少しズレるだけ)ことを理由に広く用いられているようです.その際,補正項に関しては係数をかけずに足す流派の方が主流に見受けられます.
先ほどのwB97X-D/6-31G(d)レベルで最適化した構造に対して,wB97X-D/6-311++G(2d,p)レベルでエネルギー計算を行った結果は以下のようになりました.
| level | H (kcal/mol) | G (kcal/mol) |
|---|---|---|
| wB97X-D/6-311++G(2d,p)//6-31G(d) | -1.1009 | -1.0525 |
終わりに
今回は「Psi4における振動数計算:IRスペクトルや異性体間のエネルギー差を計算」という話題に関し,psi4を用いた振動数計算について解説しました.特に,
- 振動数計算とはなにか
- Psi4を用いた振動数計算の実行と計算コスト
- 計算レベルとIRのスケールファクター
- 振動数計算より得られるエネルギー補正値
などについて説明しました.
次回は振動数計算にて得られる最適化構造の性質に関し,遷移状態の最適化について説明していきたいと思います.
>>次の記事:「Psi4で遷移状態最適化:計算化学における虚振動と化学構造」
コメント