前回の「pythonで統計学基礎: 01 平均と分散」という記事では平均・分散などの基本的な統計量をpythonを用いて,特にpandasを使うことでどのように扱うかを学びました.続いてpandasの機能を使うことで度数分布表やヒストグラムが容易に作成できることを見てきました.同時にseabornを使ったヒストグラムの作成やmatplotlibを用いてバイオリンプロットでデータを俯瞰する方法についても触れました.
このように「pythonで統計学基礎: 01 平均と分散」という記事では,主にデータ処理をほどこすことで,データの性質を理解することに主眼をおいていました.今回の記事では扱いやすくしたデータをもとにデータ分析を行っていきます.
具体的には,前回同様ハンバーガー統計学こと「統計学がわかる」を題材にして,信頼区間や統計分布についてpythonを使ってどのように表現していくかを学んでいきましょう.
ライブラリのインポート
まずは必要なライブラリをimportしておきます.
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns sns.set()
標本平均・標本分散・不偏分散と母平均・母分散
まずはサンプルサイズ10のポテトの本数をpandasのSeriesとして入力します.基本的な統計量は下のテーブルにまとめるようにpandasの関数を使って簡単に求めることが可能です.
| 基本統計量 | pandas関数 |
|---|---|
| 標本平均 | mean() |
| 標本分散 | var(ddof=0) |
| 標本標準偏差 | std(ddof=0) |
今回求めたいのは不偏分散ではなく標本分散ですのでddof=0を設定していることに注意してください.
waku_sample = pd.Series([47, 51, 49, 50, 49,
46, 51, 48, 52, 49])
print('mean: {:.2f}, var: {:.2f}, std: {:.2f}'.
format(waku_sample.mean(),waku_sample.var(ddof=0),waku_sample.std(ddof=0)))
mean: 49.20, var: 3.16, std: 1.78
実際には,得られた標本からなる標本分布を使って全体の平均(母平均)や全体の分散(母分散)を求めたいです.
その際には以下の式が役に立ちます.
$$ 標本平均 = 母平均の推定値 $$
$$ 不偏分散 = (\Sigma(データ – 平均値)^2) / (サンプルサイズ-1) = 母分散の推定値 $$
pandasにおいてはddofのパラメータによって自由度を制御しています.上のコードでは標本分散を求めたかったのでddof=0としていますが,標準設定ではddof=1なのでそのまま不偏分散を求めてくれます.
print('pop_mean: {:.2f}, pop_var: {:.2f}, pop_std: {:.2f}'.
format(waku_sample.mean(), waku_sample.var(), waku_sample.std()))
pop_mean: 49.20, pop_var: 3.51, pop_std: 1.87
区間推定
t値
区間推定において重要となる基本的なイメージは「サンプルを多くすれば誤差が少なくなる」というものです.これは我々の直感に非常に沿ったものですが,数学的にも示すことができます.
実際に標本平均から推定した母平均のばらつき,標本平均の分散は以下の式のようにサンプルサイズに依存します.
$$ 標本平均の分散 = (母分散 \div サンプルサイズ) $$
また信頼区間とは推定した値が何%の確率で存在するかを示す区間で,以下のようにt値によって決まります.標準誤差とは標本平均の標準偏差のことで,t値とはt分布という正規分布に似た形の分布から求まるもので,少ないサンプル数から母集団の性質を推定したい場合に用います.
$$ 信頼区間 = 標本平均 \pm t \times 標準誤差 $$
サンプル数が大きくなるとt分布は徐々に正規分布に近づいていきますので,サンプル数が30以上あたりからt分布ではなく正規分布を用いても問題ないとされています.今回の場合はサンプルサイズが10ですのでt分布が必要です.
以下のコードでこのことを確認してみます.tの値を5,10,30と変化させたt分布の確率密度関数と,正規分布の確率密度関数と同時にプロットしてみます.
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.linspace(-8,8,100)
for t in [5,10,30]:
t_pdf = stats.t.pdf(x=x, df=t)
ax.plot(x, t_pdf, label='t={}'.format(t))
ax.plot(x, stats.norm.pdf(x), label='norm')
ax.legend(loc='best')
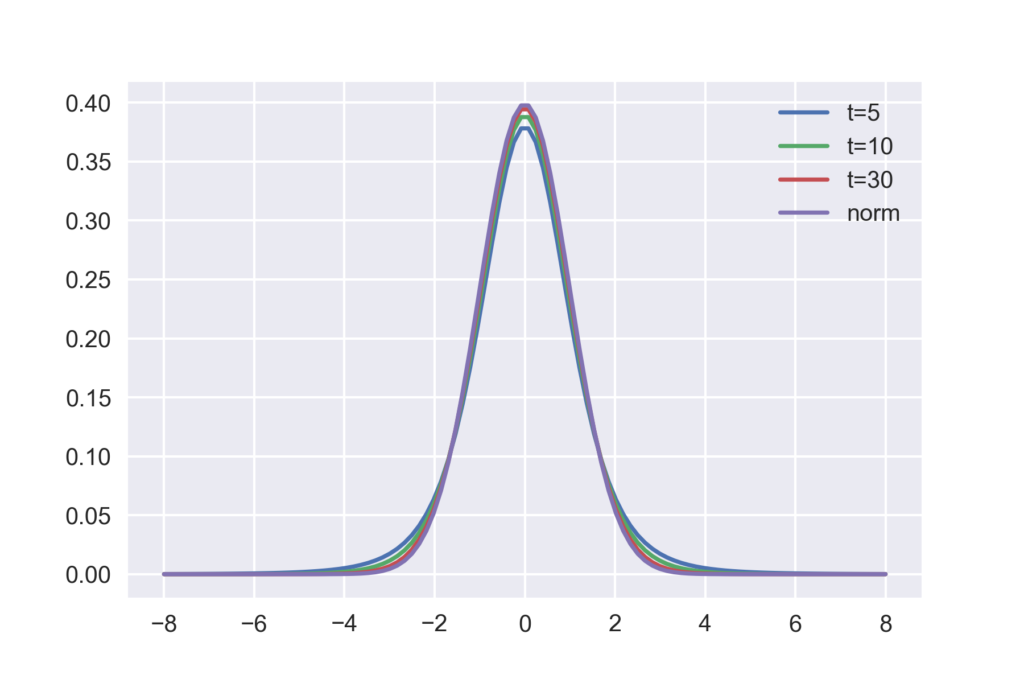
先ほど述べたようにtが30では正規分布との差がかなり小さくなっていることが見てとれます.
pythonを用いた信頼区間の決定
それでは先ほどの式に従って,t値を用いて信頼区間を求めていきますましょう.以下のコードではpythonで95%信頼区間を求めてみます.ここではscipy.statsにあるinterval関数を使っています.
alphaが求めたい区間に含まれる確率で,通常は0.95か0.99を用います.それぞれ95%,99%信頼区間に相当します.dfは自由度で,サンプルサイズから1を引いたものになります.今回はサンプルサイズ10なので自由度は9です.
from scipy import stats
t_dist = stats.t(loc=waku_sample.mean(),
scale=np.sqrt(waku_sample.var()/10),
df=9)
bottom, up = t_dist.interval(alpha=0.95)
print('95% interval: {:.2f} < x < {:.2f}'.format(bottom, up))
本と同じように95%信頼区間が求まりました.
95% interval: 47.86 < x < 50.54
終わりに
今回は標本に関する統計量を使ってどのように母集団の性質を推定していくかについて学びました.この際に大事なイメージは「標本を大きく採ればその分だけ推定の精度もよくなる」というものでした.
また推定作業の過程で正規分布に似たt分布という確率分布や,それに付随するt値という指標が出てきました.今の段階ではこの辺りのことは難しいかもしれませんが,複雑な計算もpythonがやってくれるということは理解して頂けたかと思います.
次回はさらに一歩進んで,t検定といわれるものを扱います.今回行った母集団についての推定をもとに,意思決定を行うのが検定です.
データ分析とは,
- 手元にあるデータを理解し
- 未知のものを推定し
- それに基づいた意思決定を行う
という一連の作業であり,その最終工程を扱うことになります.頑張っていきましょう.
>>次の記事:「pythonで統計学基礎:03 検定・分散分析」
コメント