本ブログで量子化学計算エンジンとして利用しているPsi4は,GitHub上にてオープンソースで開発されています。「計算化学にPythonとPsi4で入門」という記事でも述べたように,オープンソースによる開発形式の一つの利点に,有志(ときに開発者自身)により最新の計算手法がすぐに実装される点が挙げられます。
今回はPsi4のver 1.9より利用可能になった3cコンポジット法と呼ばれる手法を紹介します。ボン大学のGrimmeらが近年精力的に開発している手法です。

コンポジット法とは何か
3cコンポジット法の説明に先立ち,量子化学計算におけるコンポジット法・複合法について簡単に説明します。
分子軌道法の発展に伴って,非常に優れた精度を与える計算手法が開発されてきました。原理的にはほとんどの系では,CCSD(T)のような手法に対して,極限まで大きくした基底関数系を用いることで高精度の結果が得られます。しかしこの方法は水分子のような小さな分子であっても,計算コストが非常に高くなってしまい実用性の観点から課題を残します。
そのため,高精度な結果を外挿的に推定する方法がいくつか開発されてきました。これら方法は,より低精度・低コストの量子化学計算の結果を複数組み合わせて推定を行うことから,複合法(compound/composite method)と呼ばれます。
代表的な複合法として,
- Gaussian-n モデル(例:G2)
- CBS モデル
- Weizmann-n モデル(例:W1)
などが知られています。本記事では詳細には立ち入りませんので,興味のある方は計算化学の成書を参照してみてください。
これらモデルでは,生成エンタルピーなどの熱化学量を「化学的精度(chemical accuracy, 1 kcal/mol以内)」で見積もるために,以下のような手順を踏んでいきます。
- 分子構造を最適化する
- 中程度の精度でエネルギー計算を行い,を求める
- より高精度のエネルギー計算を複数行い,に対する補正エネルギーを求める
- 種々の経験的な補正を行う
- 振動数計算によりゼロ点補正エネルギーを求める
- エネルギー値を,各種補正エネルギー,ゼロ点エネルギーの和として求める
3cコンポジットメソッドとは
密度汎関数法(DFT)は分子軌道法と比べて計算コストが低く,かつ良好な精度が得られることから現代の量子化学計算における主流になっています。適切にDFT汎関数を選択し,トリプルゼータ以上の基底関数系を用いると高い精度で分子構造やエネルギーが得られると示されています。
しかし,現実的な系を対象とすべく何百原子もから成る分子の計算を始めると,計算コストが比較的低いDFTでさえも何十・何百も存在する配座異性体などを計算するのは困難になってきます。
分子軌道法の分野で発展してきた従来のコンポジット法の哲学を踏襲しつつ,精度を犠牲にせず・より計算コストの低い密度汎関数法を目指して開発されているのが3cコンポジット法になります。
3cコンポジット法では名前の通り3つの補正(three corrections),すなわち
- D3またはD4補正による分散力の補正
- 幾何学的CP法(gCP: geometric counter poise)による基底関数重なり誤差(BSSE)の補正
- 入念に最適化・補正された基底関数系
が適用されています。なお最新のwB97X-3cに関してはECPを用いた基底関数系を採用することでBSSEを補正しています。そのためgCPは利用していませんが,同種の哲学に基づいて開発されているため「3c」の名が付与されています。
計算に必要なライブラリのインストール
Psi4 1.9以上に加え,
- dftd3
- dftd4
- gcp
の3つのライブラリが必要です。Psi4と一緒にはインストールされないため,別途インストールが必要です。いずれもconda-forgeからインストール可能です。
なおgcpライブラリは2種類ありますが,以下のコマンドで新しい方のmctc-gcpがインストールされます。
conda install dftd3-python dftd4-python gcp-correction -c conda-forge
Psi4で利用可能な3cコンポジット法
Psi4 1.9では
- HF-3c
- PBEh-3c
- B97-3c
- r2SCAN-3c
- wB97X-3c
の5つの3cコンポジット法が実装されました。計算の実行に必要なライブラリをまとめたのが以下の表です。
なお3cコンポジット法は基底関数系も含めて最適化されているため,計算レベルの指定には「b97-3c」などと指定するだけで問題ありません。B97-3cの場合にはdef2-mTZVPが使われるなど,それぞれの手法ごとに決まった基底関数系が自動で利用されます。
| コマンド | 計算レベル | 必要なライブラリ |
|---|---|---|
| hf-3c | HF-3C/MINIX | dftd3, gcp |
| pbeh-3c | PBEh-3c/def2-mSVP | dftd3, gcp |
| b97-3c | B97-3c/def2-mTZVP | dftd3, gcp |
| r2scan-3c | r2SCAN-3c/def2-mTZVPP | dftd4, gcp |
| wb97x-3c | wB97X-3c/vDZP | dftd4 |
以下のコードでは水分子を例にB97-3cレベルでエネルギー計算をしています。
import psi4
print(psi4.__version__) # 1.9.1
psi4.set_output_file('water.log')
water = psi4.geometry("""
0 1
O -0.30493706 1.20522747 0.00000000
H 0.65506294 1.20522747 0.00000000
H -0.62539165 2.11016331 0.00000000
""")
psi4.energy('b97-3c', molecule=water)
ログファイルを眺めてみると,以下のようにb97-3cと指定しただけで対応するdef2-mTZVPが利用されていることが確認できます。
==> Primary Basis <==
Basis Set: DEF2-MTZVP
Blend: DEF2-MTZVP
Number of shells: 16
Number of basis functions: 30
Number of Cartesian functions: 32
Spherical Harmonics?: true
Max angular momentum: 2
3cコンポジット法の性質
実際に自身の系への活用を考えた際に候補となるのは,多くの場合r2SCAN-3cとwB97X-3cのいずれかだと思います。そこでこの2つの手法に絞り,wB97X-3cの元文献からこれらの性質をまとめてみます。
"ωB97X-3c: A composite range-separated hybrid DFT method with a molecule-optimized polarized valence double-ζ basis set" J. Chem. Phys. 2023, 158, 014103.
計算コスト
wB97X-3cで用いられるvDZP基底関数系はダブルゼータですが,混成汎関数であるwB97X-V自体の計算コストが高いです。そのため,メタGGA汎関数由来のr2SCAN-3cなどと比べるとトータルの計算コストは高くなります。
例えばwB97X-3cの文献では有機分子を包摂したBN-ナノチューブのエネルギー計算の例が挙げられています。一部抜粋したデータを下の表に示しています。
| 計算レベル | 計算時間 |
|---|---|
| HF-3c | 8 m |
| B97-3c | 40 m |
| r2SCAN-3c | 46 m |
| PBEh-3c | 1 h 12 m |
| wB97X-3c | 7 h 57 m |
| wB97X-V | 37 h 57 m |
<文献(J. Chem. Phys. 2023, 158, 014103.)のFig. 3より抜粋>
適用範囲
論文では種々のベンチマーク用のデータセットに対して,r2SCAN-3cとwB97X-3cに加え,代表的なDFT汎関数(B97M-V,B3LYP-D4,wB97X-V,wB97X-D4)とQZ基底系を組み合わせた結果がまとめられています。
理論開発ではない論文では,DZ基底系での構造最適化,TZ基底系でのエネルギー計算が主流であることを考慮すると,かなり大きな基底系との比較であることに注意してください。
論文から伺える傾向は以下のようになります。
- 典型元素から成る分子系では総合的にはwB97X-3cの方が優れた精度を与えている
- 非結合性相互作用を含む系は両手法に特徴がある
- 配座異性体間のエネルギー差はr2SCAN-3cの方がよい
- 反応のエネルギー差はどちらも同程度の精度
- 遷移状態エネルギーはwB97X-3cの方が明らかによい
- 遷移金属を含む系ではr2SCAN-3cの方がよい
- 計算コストを踏まえると構造最適化に関してはr2SCAN-3cが推奨される
Psi4を使った計算の具体例
具体的な特徴がわかったところで,Psi4を用いた計算を行ってみます。ここではWeinrebアミドの2つの配座のエネルギー差を計算してみます。なお窒素上の酸素原子がカルボニル基と反対側に位置するtrans 型(下のコードのamide1)の方が安定と知られています。
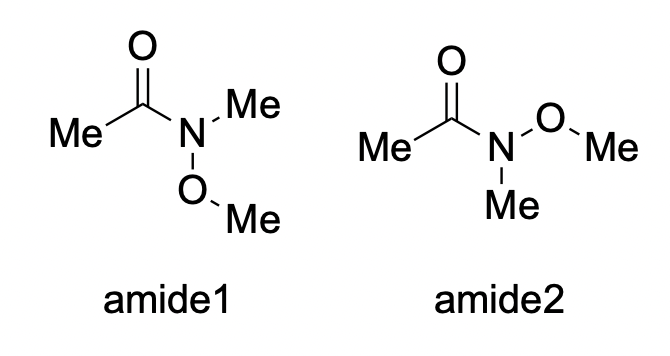
以下のコードでは
- 2つの配座をwB97X-D/def2-SVPレベルで構造最適化
- 最適化構造に対してwB97X-V/def2-TZVPPレベルでエネルギー計算を行い,実行時間とエネルギー差を出力
- 同様にr2SCAN-3cレベルでエネルギー計算を行い,実行時間とエネルギー差を出力
- 同様にwB97X-3cレベルでエネルギー計算を行い,実行時間とエネルギー差を出力
という順番で処理を行っています。
なお前述のようにwB97XD-3cでは基底関数重なり誤差の修正にgCPではなく,ECPを用いているためエネルギーの絶対値のオーダーが他の手法とは異なります。相対エネルギー差のみに注目してください。
import time
import psi4
psi4.set_num_threads(12)
psi4.set_memory('16gb')
au2kcal = psi4.constants.hartree2kcalmol
amide1 = psi4.geometry("""
0 1
C -1.49368857 0.86255258 0.00000000
O -2.11522757 -0.21398342 0.00000000
N -0.12751157 0.90898958 0.00000000
C -2.19058762 2.23584487 0.00002626
H -1.90369585 2.78137900 0.87466082
H -1.90068625 2.78293968 -0.87263890
H -3.25158968 2.09738613 -0.00192492
C 0.66367145 -0.32993311 0.00000149
H 0.43052756 -0.90201103 -0.87365221
H 1.70586242 -0.08757394 0.00000734
H 0.43051922 -0.90201486 0.87365045
O 0.53646293 2.09589220 -0.00017376
C 1.83254097 1.91788699 0.57723066
H 2.46631096 1.40925708 -0.11885210
H 2.25345026 2.87359404 0.81038167
H 1.74765390 1.33761716 1.47220614
""")
amide2 = psi4.geometry("""
0 1
C -1.49368857 0.86255258 0.00000000
O -2.11522757 -0.21398342 0.00000000
N -0.12751157 0.90898958 0.00000000
C -2.19058762 2.23584487 0.00002626
H -1.90369585 2.78137900 0.87466082
H -1.90068625 2.78293968 -0.87263890
H -3.25158968 2.09738613 -0.00192492
C 0.57775027 2.19786880 -0.04791762
H 0.30518860 2.78546221 0.80375375
H 1.63398759 2.02698446 -0.04009017
H 0.30742824 2.71932312 -0.94229527
O 0.61549551 -0.22924702 0.04424829
C 1.89724349 0.01433807 -0.54114765
H 2.49413077 0.59079811 0.13436652
H 2.38235326 -0.91873336 -0.73849563
H 1.77431619 0.55321238 -1.45733724
""")
## optimize at wb97x-d/def2-svp
theory = 'wb97x-d/def2-svp'
psi4.set_output_file('weinreb_opt.log')
psi4.optimize(theory, molecule=amide1)
psi4.optimize(theory, molecule=amide2)
## get energies
psi4.set_output_file('weinreb_wb97xvTZ.log')
t1 = time.time()
e1_wb97xv = psi4.energy('wb97x-v/def2-tzvpp', molecule=amide1)
e2_wb97xv = psi4.energy('wb97x-v/def2-tzvpp', molecule=amide2)
t2 = time.time()
print(f'elapsed time with wB97X-V/def2-TZVPP: {t2 - t1: .3f} s')
print(f'energy difference at wB97X-V/def2-TZVPP {(e2_wb97xv - e1_wb97xv) * au2kcal:.3f} kcal/mol')
psi4.set_output_file('weinreb_r2scan3c.log')
t1 = time.time()
e1_r2scan = psi4.energy('r2scan-3c', molecule=amide1)
e2_r2scan = psi4.energy('r2scan-3c', molecule=amide2)
t2 = time.time()
print(f'elapsed time with r2SCAN-3c: {t2 - t1: .3f} s')
print(f'energy difference at r2SCAN-3c: {(e2_r2scan - e1_r2scan) * au2kcal:.3f} kcal/mol')
psi4.set_output_file('weinreb_wb97x3c.log')
t1 = time.time()
e1_wb97x = psi4.energy('wb97x-3c', molecule=amide1)
e2_wb97x = psi4.energy('wb97x-3c', molecule=amide2)
t2 = time.time()
print(f'wB97X-3c: {t2 - t1: .3f} s')
print(f'energy difference at wB97X-3c: {(e2_wb97x - e1_wb97x) * au2kcal:.3f} kcal/mol')
結果は以下のようになりました。全ての計算レベルでtrans 体の方が3 kcal/mol前後安定と示されました。予想と異なりwB97X-3cが最も計算時間が短かったですが,いずれの3cコンポジット法もTZ基底系を用いた通常のDFT計算よりも速いことが確認できました。
elapsed time with wB97X-V/def2-TZVPP: 55.651 s energy difference at wB97X-V/def2-TZVPP 2.928 kcal/mol elapsed time with r2SCAN-3c: 12.072 s energy difference at r2SCAN-3c: 3.054 kcal/mol wB97X-3c: 10.206 s energy difference at wB97X-3c: 3.137 kcal/mol
終わりに
今回は「Psi4で3cコンポジット法を利用する」という話題について,
- 3cコンポジット法とは何か
- 3cコンポジット法の性質・特徴
- Psi4で利用可能な3cコンポジット法
などについて説明し,具体的な計算例を通して利用方法を見てきました。
新しい手法が発表後さほど時間を経たずに実装される点は,活発に開発が行われているオープンソースソフトウェアの大きな利点です。
r2SCAN-3cやwB97X-3cは高い精度の計算結果を低コストで取得できる魅力的な方法だと思います。世界一のシェアを誇るGaussianにも未だ実装されていない計算手法をPsi4で経験してみましょう。

コメント