「計算化学における電荷:Psi4を用いた電子密度解析」という記事では,波動関数から得られる情報として電子密度解析のやり方を説明しました.今回は波動関数から得られる他の情報として,分子軌道や静電ポテンシャルなどの対象分子を中心とした3次元空間に広がる情報を取り扱っていきます.
今回の記事では
- まず3次元空間に広がる値を記録するフォーマットとして一般的な「Cubeファイル」を紹介し,
- その後Psi4を用いて波動関数から取得可能な各種情報を概説,
- 最後にJupyterノートブックやPyMOL上で可視化する方法について紹介
していきたいと思います.

Gaussian Cubeファイルとは
Cubeファイルとは一定の規則で記述されるテキストファイルで,分子を中心とした3次元空間に広がる値を格納するためのファイルフォーマットです.Gaussian社が最初に使い始めことから,Gaussian Cubeファイルとも呼ばれますが,多くの計算化学関係ソフトで取り扱いが可能な事実上の標準フォーマットになっています.
Cubeファイルは格納されている値の基本情報を記した「ヘッダー」部分と,値そのものを並べた「データ」部分に分かれています.ヘッダー部分はさらに細かくいくつかの部分に分けられます.
Cubeファイルのヘッダー部位の構造
ヘッダー部位は以下のような構造になっています.
コメント行1 コメント行2 原子数,原点の座標 x軸に関する,座標数とその差分(ボーア) y軸に関する... z軸に関する... 原子1の原子番号,電荷,xyz座標(ボーア) ・・・ 原子nの原子番号,電荷,xyz座標(ボーア)
これだけではわかりにくいと思うのでpsi4で計算したベンゼンの分子軌道のヘッダー部位の例も示します.
Psi4 Gaussian Cube File.
Property: Psi_a_22_22-A. Isocontour range for 85% of the density: (0.0482584,-0.0482759)
12 -8.499995 -8.599996 -4.100009
86 0.200000 0.000000 0.000000
87 0.000000 0.200000 0.000000
42 0.000000 0.000000 0.200000
6 0.000000 -2.513403 -0.742953 -0.000001
6 0.000000 -0.613192 -2.548171 0.000028
6 0.000000 1.900117 -1.805194 -0.000035
6 0.000000 2.513375 0.743046 0.000004
6 0.000000 0.613286 2.548149 0.000030
6 0.000000 -1.900184 1.805124 -0.000020
1 0.000000 -4.475099 -1.322929 -0.000010
1 0.000000 -1.091891 -4.537008 0.000003
1 0.000000 3.383241 -3.214083 -0.000047
1 0.000000 4.475109 1.322897 -0.000013
1 0.000000 1.091858 4.537016 0.000020
1 0.000000 -3.383218 3.214107 -0.000027
- 1,2行目はコメント行になります.1行目が主に作成した環境(ソフト)などの情報を,2行目がCubeファイル自体の情報(どんなデータが格納されているか)について記載されていることが多いです.
- 3行目は対象とする分子の原子数,及び対象空間の座標原点が記されています.
- 4−6行目ではxyz各軸に関し,グリッド数とその大きさが記されています.例えばX軸方向には(0.2, 0.0, 0.0)の大きさのグリッドを86点取ります.必ずしも各軸とは平行である必要はなさそうですが,通常は軸に沿ったグリッドになっています.
- 7行目以降が各原子に関する情報になっています.
なお座標データの単位系は全てボーアです.
Cubeファイルのデータ部位の構造
データ部位はグリッド(0, 0, 0) (0, 0, 1), (0, 0, 2),・・・に関するデータが次々と出力されています.慣習的に6グリッドごとに改行されます.同様に上記のベンゼンのデータの冒頭部を抜粋します.
1.15164E-12 1.56216E-12 2.07655E-12 2.70419E-12 3.44871E-12 4.30552E-12 5.25937E-12 6.28242E-12 7.33325E-12 8.35714E-12 9.28800E-12 1.00522E-11 1.05740E-11 1.07824E-11 1.06187E-11 1.00437E-11 9.04428E-12 7.63699E-12 5.86966E-12 3.81909E-12 1.58580E-12 -7.14173E-13 -2.95920E-12 -5.03276E-12 -6.83344E-12 -8.28313E-12 -9.33244E-12 -9.96294E-12 -1.01860E-11 -1.00388E-11 -9.57843E-12 -8.87421E-12 -8.00058E-12 -7.03014E-12 -6.02820E-12 -5.04901E-12 -4.13378E-12 -3.31038E-12 -2.59427E-12 -1.99037E-12 -1.49550E-12 -1.10076E-12 1.77994E-12 2.41749E-12 3.21669E-12 4.19195E-12 5.34853E-12 6.67862E-12 ・・・後略・・・
実際はこのような数値データが86 x 87 x 42個並んでいることになります.
Psi4とCubeファイル
Psi4においてCubeファイルを作成するにはcubepropを使います.事前にどんな内容のファイルを作成するかをオプションで設定することで,様々なファイルを出力することが可能になっています.
cubeprop_tasksオプション
Psi4のcubepropを用いて出力可能なcubeファイルの種類は以下の通りです.cubeprop_tasksオプションでどのファイルを出力するかを指定します.
静電ポテンシャル(ESP)や分子軌道(orbitals)といった有名なものから,やや特殊なものまで色々含まれています.
| cubeprop_tasks | 出力されるcubeファイル |
|---|---|
| density | Da, Db, Dt, Ds |
| esp | Dt, ESP |
| orbitals | Psi_a_N, Psi_b_N |
| basis_functions | Phi_N |
| lol | LOLa, LOLb |
| elf | ELFa, ELFb |
| frontier_orbitals | Psi_a_N_HOMO, Psi_a_N_LUMO |
| dual_descriptor | DUAL_N_HOMO-M_LUMO |
注意点としては,
- フロンティア軌道で出力されるのはalpha electronのみ(Psi_a)
- 分子が大きくなると軌道数が多くなるため,どの軌道を出力するかをcubeprop_orbitalsオプションで別途指定しないと大量のファイルが出力されることになる
などが挙げられます.
分子軌道とESPについては以下で具体的にコードを用いて見ていきます.他のものについては,興味のある方は以下の文献などを参照して下さい.
- LOL: localized-orbital locator
Chemical content of the kinetic energy density
J. Mol. Struct.: THEOCHEM 2000, 527, 51-61. -
ELF: electron localization function
A simple measure of electron localization in atomic and molecular systems
J. Chem. Phys. 1990, 92, 5397. -
Dual Descriptor
New Dual Descriptor for Chemical Reactivity
J. Phys. Chem. A 2005, 109, 205–212.
cubeprop_filepathオプション
出力ファイルをどこに保存するかを指定します.分子によらず出力ファイル名は同じですので,例えば多くの分子を一度に計算したい場合などは,それぞれ別のフォルダに保存する必要があります.
cubeprop_orbitalsオプション
cubeprop_tasksオプションの「orbitals」と組み合わせて利用し,どの軌道を出力するかをリストで指定します.正の数字がアルファスピン電子,負の数字がベータスピン電子オービタルです.上述のようにデフォルトでは全ての軌道が出力されます.
Psi4を用いて分子軌道とESPのCubeファイルの作成
今回は以下のような設定で,「.py」ファイルを用いて計算を行っていきます.手元のコンピュータで実行する際には,各自の環境に応じてメモリ使用量などを修正してみてください.
import sys
import pathlib
import psi4
filename = pathlib.Path(__file__)
logfile = filename.with_suffix('.log').name
psi4.set_output_file(logfile)
psi4.set_memory('14GB')
psi4.set_num_threads(12)
print(f'python version:\n{sys.version}')
# python version:
# 3.9.7 (default, Sep 16 2021, 13:09:58)
# [GCC 7.5.0]
print(f'psi4 version:\t{psi4.__version__}')
# psi4 version: 1.5
分子軌道
‘cubeprop_orbitals’: [-n, n]})
下記のコードでは,ベンズアルデヒドを例に
- B3LYP/6-31G(d)レベルで構造最適化と振動数計算
- 最適化構造に対してHF/STO-3GとHF/6-311+G(d,p)レベルでエネルギー計算
- それぞれのエネルギー計算で得たWavefunctionファイルからHOMOとLUMOのcubeファイルを出力
という作業をしています.
閉殻分子ですので,HOMOの軌道番号はαスピン電子数(nalpha)から求めています.
geom = '''
0 1
C -2.21030032 -0.80829756 0.00000000
C -0.81514032 -0.80829756 0.00000000
C -0.11760232 0.39945344 0.00000000
C -0.81525632 1.60796244 -0.00119900
C -2.21008132 1.60788444 -0.00167800
C -2.90768232 0.39967844 -0.00068200
H -2.76005932 -1.76061456 0.00045000
H -0.26563232 -1.76081056 0.00131500
H -0.26505632 2.56010544 -0.00125800
H -2.76020332 2.56016544 -0.00263100
H -4.00728632 0.39986144 -0.00086200
C 1.42239742 0.39956548 0.00088786
O 2.07678170 1.43787575 0.00091940
H 1.90141156 -0.60226316 0.00153664
'''
phcho: psi4.core.Molecule = psi4.geometry(geom)
opt_level = 'b3lyp/6-31g(d)'
print('##\tOptimization')
_, wfn = psi4.optimize(opt_level,
molecule=phcho,
return_wfn=True)
print('##\tFrequency')
_, wfn = psi4.frequency(opt_level,
molecule=phcho,
ref_gradient=wfn.gradient(),
return_wfn=True)
print(f'\nOptimized Structure\n{phcho.save_string_xyz()}')
n_alpha = wfn.nalpha()
cubeprop_paths = ['phcho/hf_sto-3g', 'phcho/hf_6-311+gdp']
cubeprop_theories = ['hf/sto-3g', 'hf/6-311+g(d,p)']
psi4.set_options({'cubeprop_tasks': ['orbitals'],
'cubeprop_orbitals': [-n_alpha, -(n_alpha + 1), n_alpha, n_alpha + 1]})
print('##\tCubeprop')
for path, level in zip(cubeprop_paths, cubeprop_theories):
pathlib.Path(path).mkdir(parents=True, exist_ok=True)
psi4.set_options({'cubeprop_filepath': path})
print(f'\tlevel = {level}')
_, wfn = psi4.energy(level,
molecule=phcho,
return_wfn=True)
psi4.cubeprop(wfn)
PyMOLによる分子軌道の可視化
得られたcubeファイルをPyMOLで可視化してみます.PyMOL上のターミナルで下記のように入力して,HOMOを表示します.ファイル番号を変えることで同様にLUMOも可視化可能です.
下記のようなpythonスクリプトを用意して読み込み,「moViz」関数を定義することで,指定した軌道番号を可視化できます.
from pymol import cmd
def moViz(orbital: int, isoval:float=0.003):
mo_a = f'Psi_a_{orbital}_{orbital}-A.cube'
cmd.load(mo_a)
mo_b = f'Psi_b_{orbital}_{orbital}-A.cube'
cmd.load(mo_b)
cmd.isosurface('surface_a', pathlib.Path(mo_a).stem, isoval)
cmd.isosurface('surface_b', pathlib.Path(mo_b).stem, f'-{isoval}')
cmd.color('red', 'surface_a')
cmd.color('blue', 'surface_b')
cmd.set('transparency', 0.6)
cmd.extend('moViz', moViz)
もちろん各ステップを以下のようにPyMOLのターミナル上で処理することも可能です.
load geom.xyz load Psi_a_28_28-A.cube load Psi_b_28_28-A.cube isosurface homo_a, Psi_a_28_28-A, 0.003 isosurface homo_b, Psi_b_28_28-A, -0.003 color red, homo_a color blue,homo_b set transparency,0.6
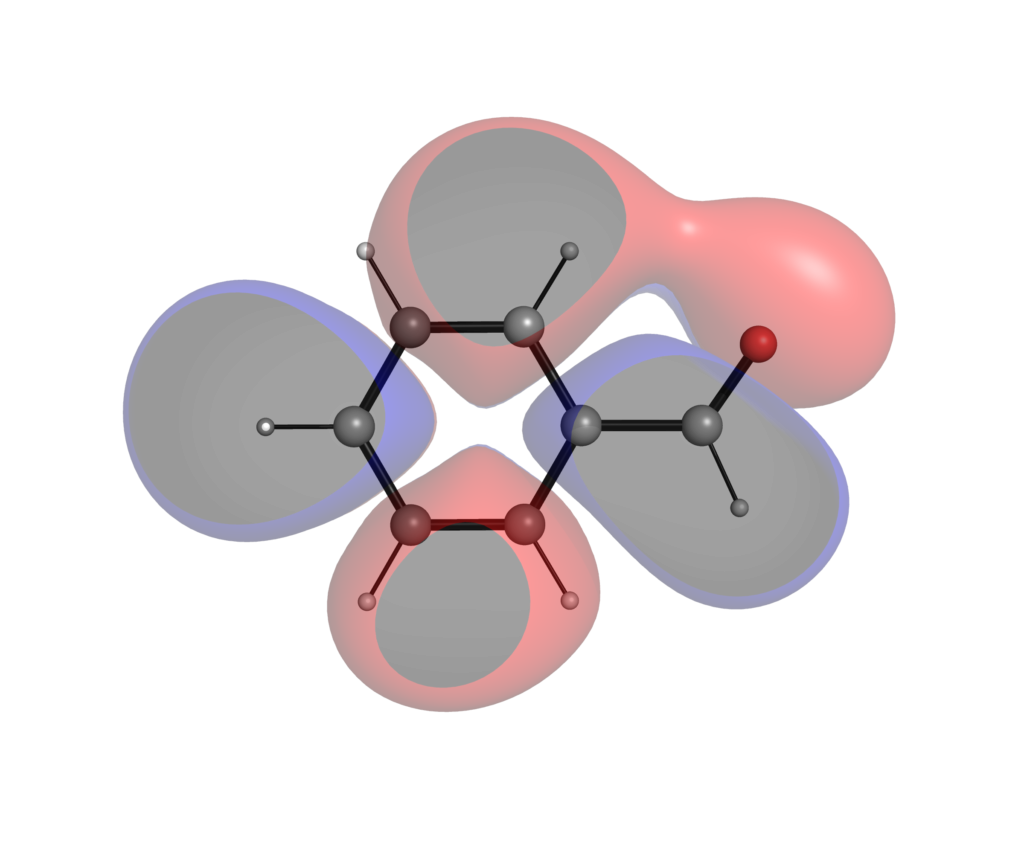
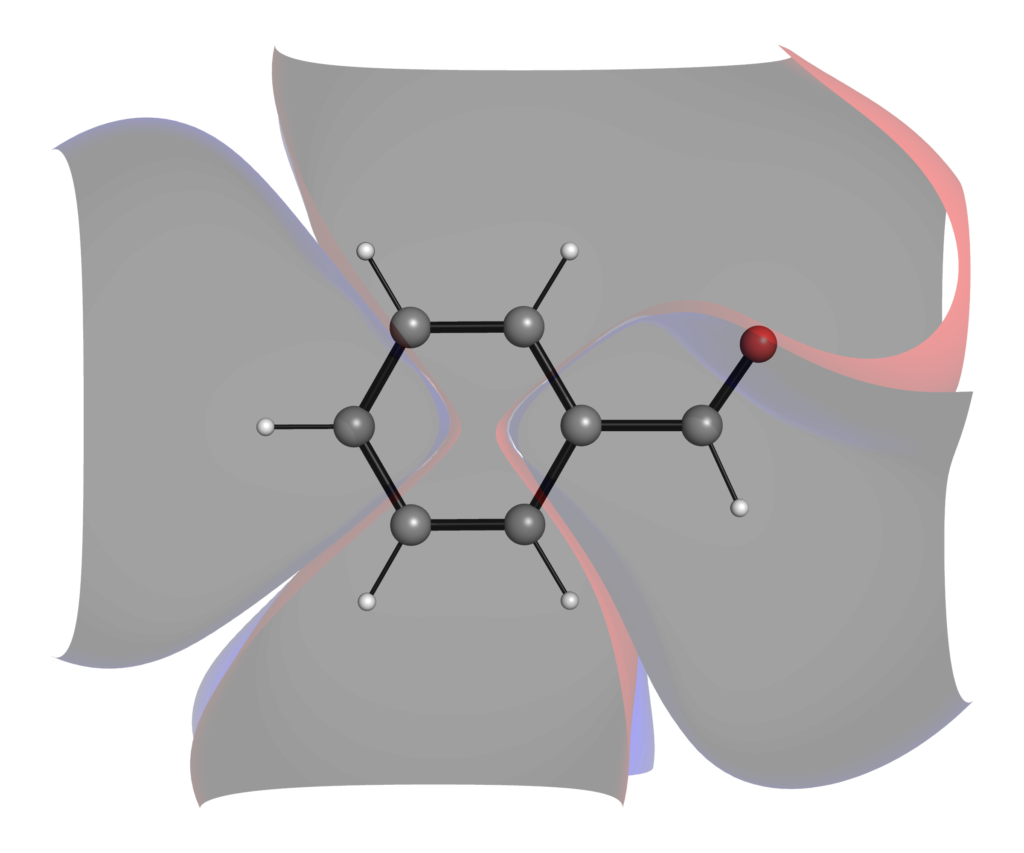
以下がSTO-3Gで計算したフロンティア軌道です.最初がHOMO,次がLUMOです.

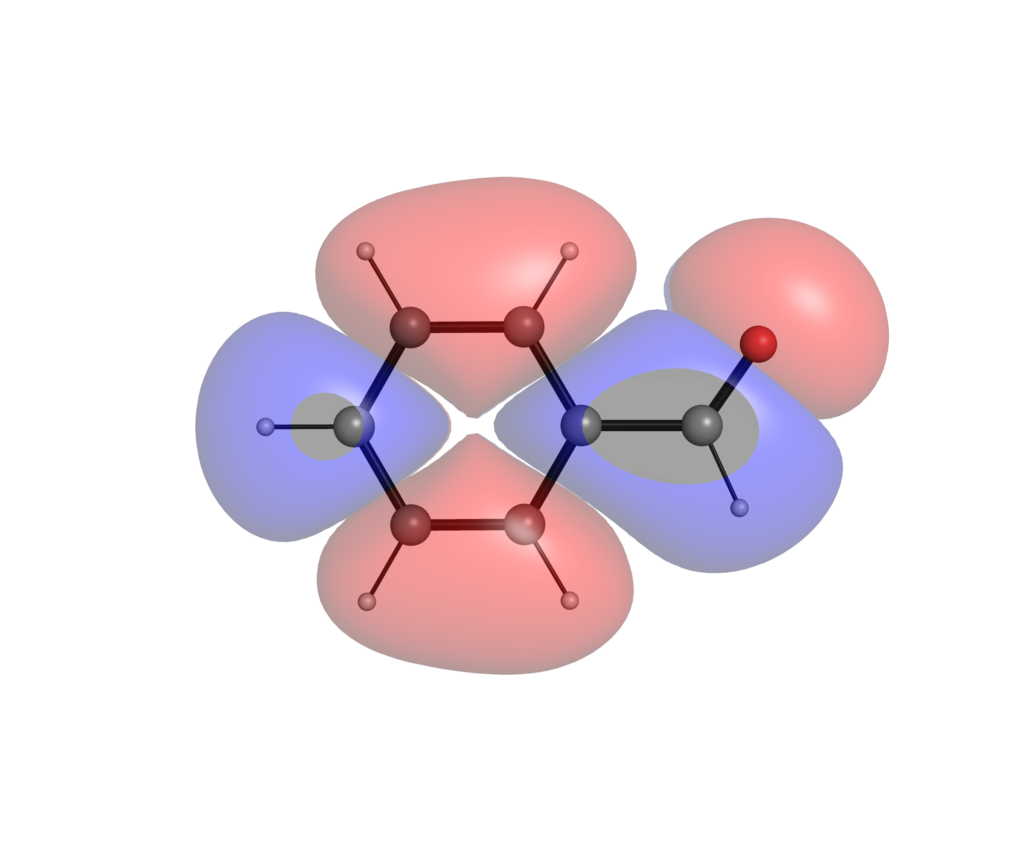
同様にこちらが6-311+G(d,p)レベルで計算したフロンティア軌道です.
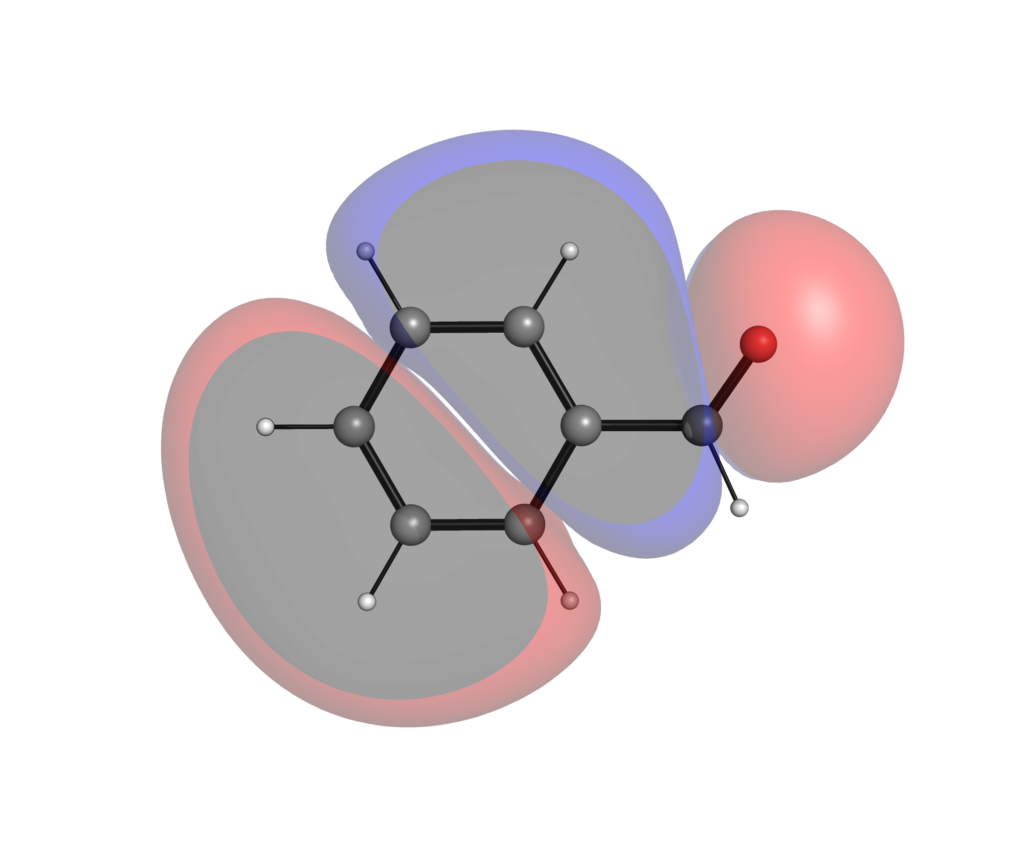
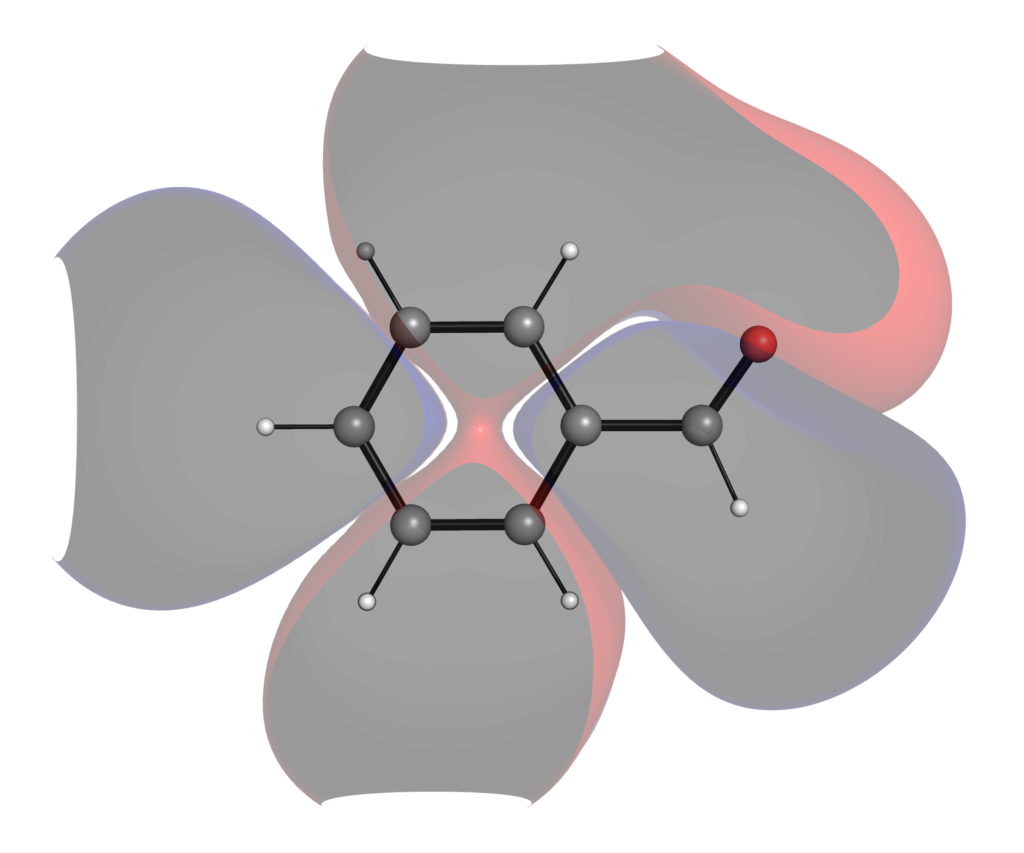
高精度で計算した方が,軌道が広がっているのがわかるでしょうか?分極関数やdiffuse関数を盛り込んだ計算レベルでは,特に非占有軌道に関しては分子の外にまで軌道が広がってしまい,軌道の形から反応性の議論がしにくいことがあります.こういった定性的な議論においては最小基底関数系程度のレベルによる可視化で十分な場合が多いです.
もちろんHOMO-LUMOギャップの値が知りたいなど,軌道エネルギーの絶対値が大切な場合は高精度の計算レベルで実施することが望ましいです.
なお軌道の形は,可視化する際の等高線の設定でも変わってきます.下の例は高精度の計算レベルのLUMOをそれぞれ0.1, 0.01, 0.001のisoval値で可視化したものになります.等高線の設定を粗くすることで,分子の外に広がる枝葉の部分を切り落とすことができています.
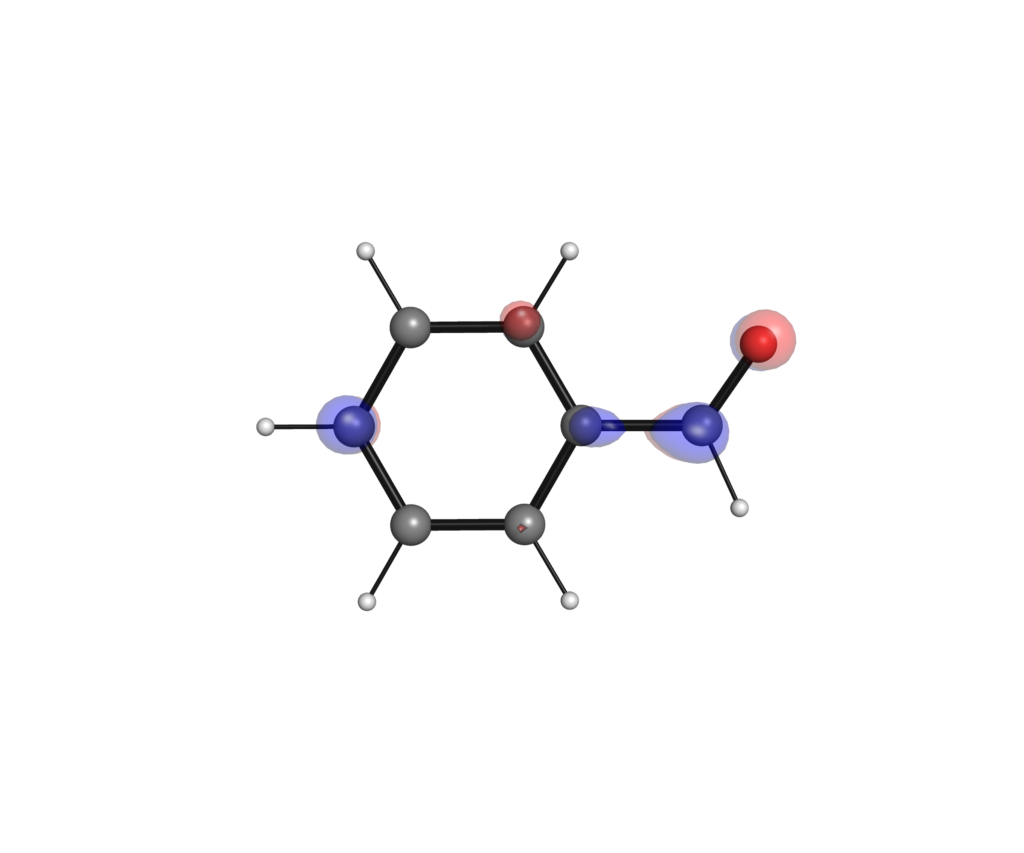
py3Dmolによる分子軌道の可視化
py3Dmolではviewerに対してaddVolumetricDataを用いることでcubeファイルの可視化が可能です.
設定項目も
- 閾値
- 色
- 透過度
とpyMOLの場合と同じです.
以下のコードでは,上記のSTO-3Gで得たファイルに関して,py3Dmol上でHOMOとLUMOの可視化を行っています.まずはデータを読み込みます.
import py3Dmol
def load_orbital(orbital_number: int):
file_a = f'Psi_a_{orbital_number}_{orbital_number}-A.cube'
file_b = f'Psi_b_{orbital_number}_{orbital_number}-A.cube'
with open(file_a, 'r') as f:
orbital_a = f.read()
with open(file_b, 'r') as f:
orbital_b = f.read()
return (orbital_a, orbital_b)
with open('geom.xyz', 'r') as f:
geom = f.read()
homo_a, homo_b = load_orbital(28)
lumo_a, lumo_b = load_orbital(29)
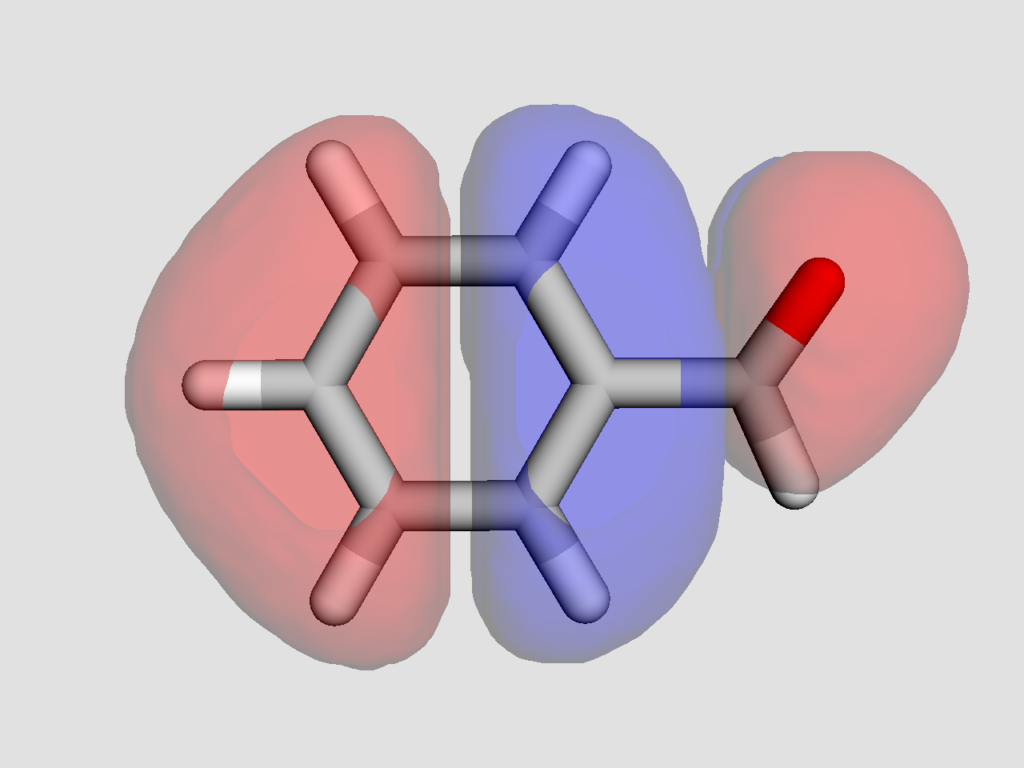
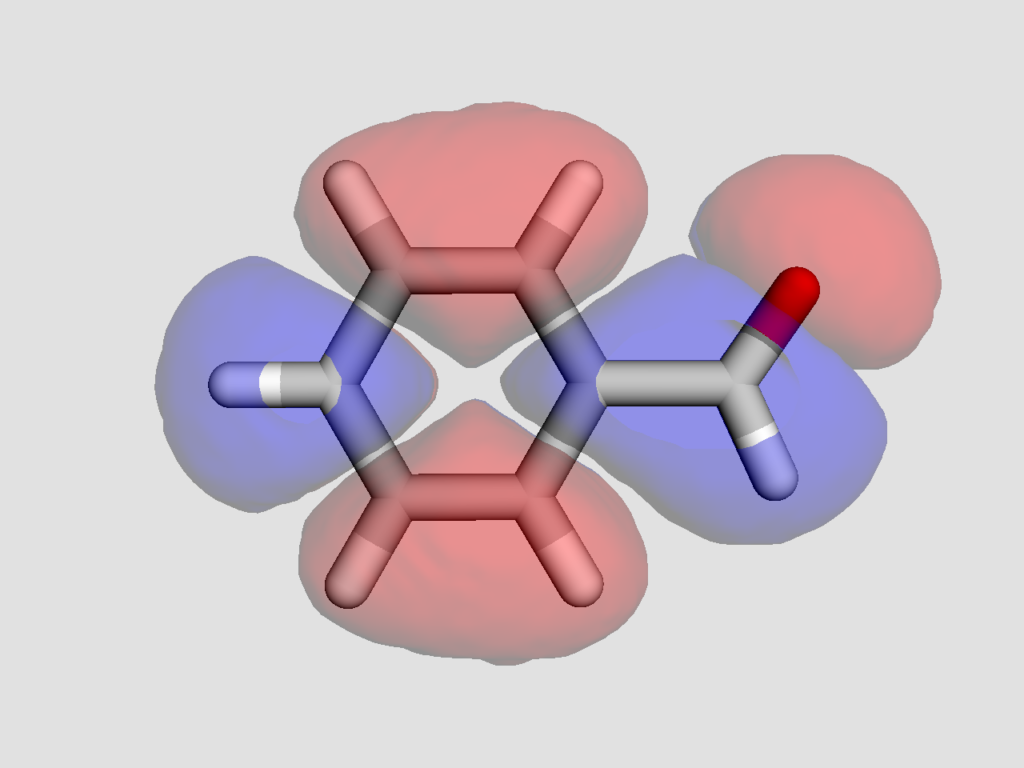
続いてHOMOの可視化を行います.LUMOも同様にして可視化可能です.
view = py3Dmol.view()
view.addModel(geom, 'xyz')
view.addVolumetricData(homo_a, 'cube', {'isoval': 0.003, 'color': 'red', 'opacity': 0.6})
view.addVolumetricData(homo_b, 'cube', {'isoval': -0.003, 'color': 'blue', 'opacity': 0.6})
view.setStyle({'stick': {}})
view.setBackgroundColor('#e1e1e1')
view.zoomTo()
view.show()
得られた結果以下のようになりました.
静電ポテンシャル
ある分子の周りに+1価の電荷を置いた際に,その電荷が感じるポテンシャルエネルギーを静電ポテンシャル(Electrostatic Potential)といいます.
低分子の静電ポテンシャルを可視化する場合には,電子密度に対してマッピングする方法が一般に使われます.そのためPsi4でもESP.cubeに加え,Dt.cubeが出力されます.一方でタンパク質などの高分子ではSAS(Solvent Accessible Surface)に対してマッピングするのが一般的です.
ここではPyMOLを用いて二つの方法で可視化してみます.アニソールとシアノベンゼンを例として,どのように静電ポテンシャルに違いがあるかを見てみます.
下記のコードはアニソールに対して,
- B3LYP/6-31G(d)レベルで構造最適化と振動数計算
- 同レベルでCubeファイルの作成
を行っています.
anisole = psi4.geometry('''
0 1
C -0.21329364 0.14880952 0.00000000
C 1.18186636 0.14880952 0.00000000
C 1.87940436 1.35656052 0.00000000
C 1.18175036 2.56506952 -0.00119900
C -0.21307464 2.56499152 -0.00167800
C -0.91067564 1.35678552 -0.00068200
H -0.76305264 -0.80350748 0.00045000
H 1.73137436 -0.80370348 0.00131500
H 1.73195036 3.51721252 -0.00125800
H -0.76319664 3.51727252 -0.00263100
H -2.01027964 1.35696852 -0.00086200
C 3.93221866 2.60510499 0.74253311
H 4.97885843 2.49904274 0.93797105
H 3.76849598 3.47200259 0.13707178
H 3.40560762 2.71168661 1.66785531
O 3.41940410 1.35667255 0.00088786
''')
level = 'b3lyp/6-31g(d)'
print('##\tstart optimization\t##')
_, wfn = psi4.optimize(level, molecule=anisole, return_wfn=True)
print('##\tstart frequency calculation\t##')
_, wfn = psi4.frequency(level, molecule=anisole, ref_gradient=wfn.gradient(), return_wfn=True)
psi4.set_options({'cubeprop_tasks': ['esp']})
print('##\tcubeprop computation\t##')
psi4.cubeprop(wfn)
電子密度に対するマッピング
得られた結果をPyMOLで可視化してみます.下記のようなpythonスクリプトでESPを可視化する「espViz」関数を定義してみました.ポイントは,
- 電子密度を用いてsurface(esp1)を作成
- ESPの値に合わせたカラースキーム(ramp)を作成
- 作成したsurfaceの色にESPの値を反映
です.
from pymol import cmd
def espViz(isoval:float = 0.003, r:float = 0.01):
cmd.load('Dt.cube')
cmd.load('ESP.cube')
cmd.isosurface('esp1', 'Dt', isoval)
cmd.ramp_new('ramp', 'ESP', f'[-{r}, 0, {r}]')
cmd.color('ramp', 'esp1')
cmd.set('transparency', 0.6)
cmd.extend('espViz', espViz)
得られたアニソール静電ポテンシャルマップは以下の通りです.同様の方法で得たシアノベンゼンの結果も載せておきます.
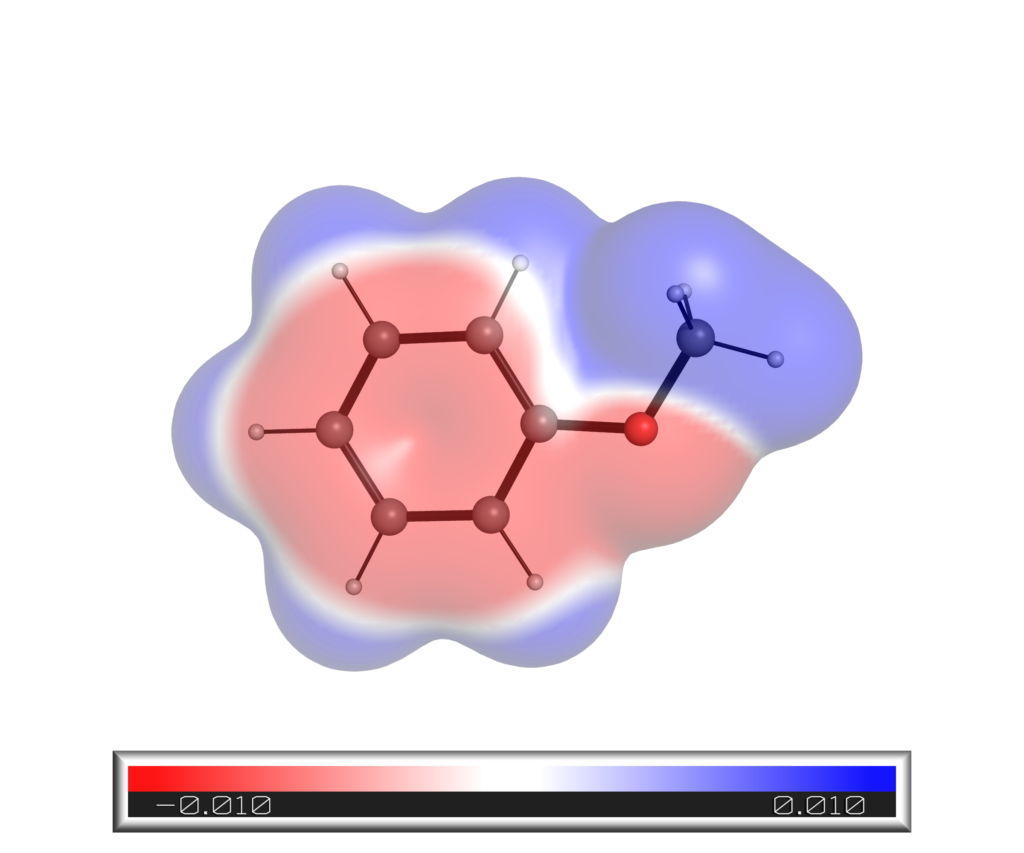
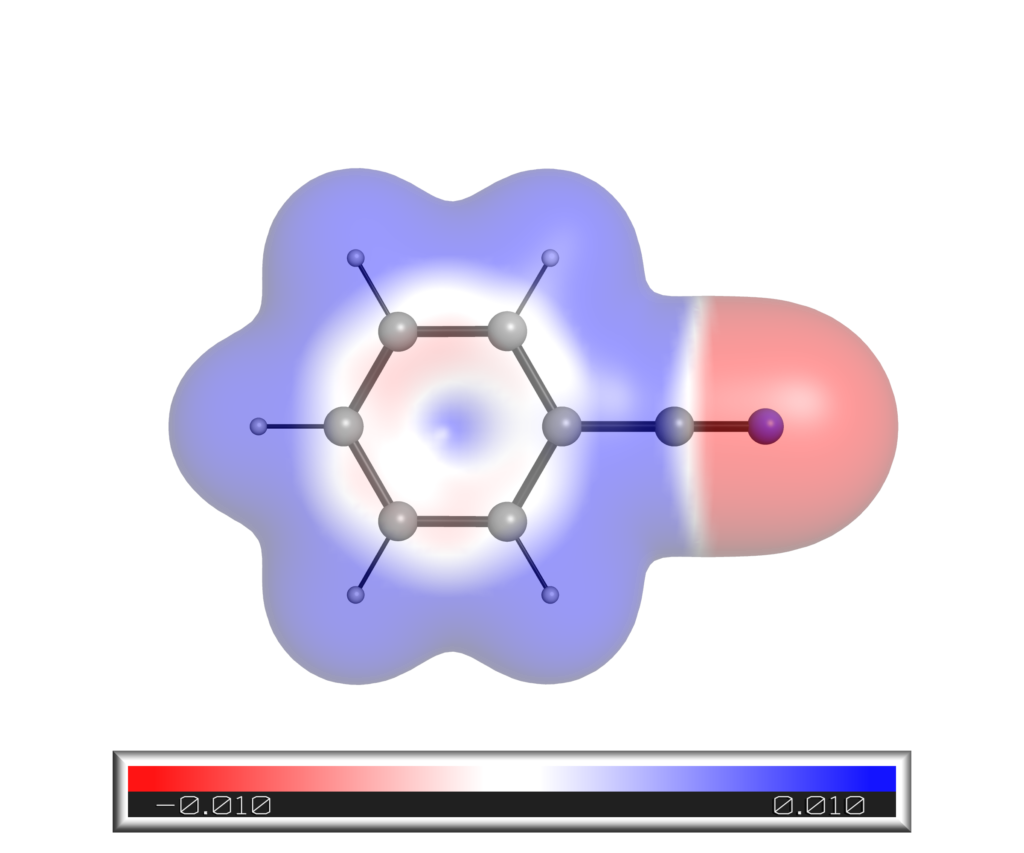
SASに対するマッピング
今度はPyMOL上で,ESPの値をSASにマッピングしてみます.今度はPyMOLの標準機能を用いてSASを表示します.
- ESPの値に合わせたカラースキーム(esp)を作成
- PyMOLの機能で分子表面を表示(show surface)
- surfaceの色にESPの値を反映
- SAS上に色をつけるモードに変更(above)
といった作業をPyMOLコンソール上で順番に行っています.
load geom.xyz load ESP.cube ramp_new espramp, ESP, [-0.003, 0, 0.003] show surface set surface_color, espramp set surface_ramp_above_mode set transparency, 0.6, geom
アニソールの結果が以下になります.電子密度にマッピングした場合と比べると「角」が少ない形になっています.

終わりに
今回は「Psi4とCubeファイル:分子軌道や静電ポテンシャルマップの可視化」という話題について,
- 空間に広がる情報を記録する「Cubeファイル」というフォーマット
- Psi4を用いて波動関数から取得可能な各種情報
- JupyterノートブックやPyMOL上でCubeファイルを可視化する方法
について説明しました.特に分子軌道とESPについては簡単な分子を用いて,PyMOL上での可視化を重点的に扱いました.
コメント
本当に基本的な事ですみません。
HOMO,LUMOの順位はどうやれば分かるのでしょうか。
例えばpy3Dmolで可視化するコードの
homo_a, homo_b = load_orbital(28)
lumo_a, lumo_b = load_orbital(29)
の28や29のことです。
ご質問ありがとうございます。
閉殻の分子ではエネルギーが低い軌道から順番に,αスピンとβスピン電子が1つずつ入ります。
そのためαスピン電子の数が占有軌道の数に一致します。
コードでは”n_alpha = wfn.nalpha()”でαスピン電子数を求めています(コード例だと28)。
この値がHOMOの軌道番号,1を加えたものがLUMOの軌道番号になります。
記事中でpy3Dmolを利用している箇所では「28」と手打ちしていますが,
これを「n_alpha」としても同じ結果になります。
大変勉強になる記事をありがとうございます。
質問なのですが,isoval = 0.003 は,どのようにして決めていますか?
コメントありがとうございます。結論としては,いくつか試した中で一番良さそうなものを選んでいます。
本文にも記しましたが,isovalの値を変えると描画される軌道の粗さ・形状が変わってきます。ご自身でも例えば,0.3, 0.03, 0.003など値を変えながら描画して頂けると,isovalの値が結果に与える影響をご理解頂けると思います。
今後ともよろしくお願いいたします。