「Psi4における振動数計算:IRスペクトルや異性体間のエネルギー差を計算」という記事では,python用量子化学計算ライブラリであるPsi4を用いた振動数計算について説明しました.その際,振動数計算は最適化構造を用いて実施する必要があることを述べました.振動数計算によって用いた最適化構造が「安定構造(極小値)」か「遷移状態(極大値)」かを知ることができます.今回は「Psi4を用いた遷移状態の最適化」について見ていくこととします.
X線結晶構造解析やクライオ電子顕微鏡などの進展によって,様々な状態の化学構造を見ることが可能になりました.それでも観測可能なものは基本的に安定構造のみであるため,「遷移状態」を見ることが可能な点は計算化学の大きな利点です.
例えば最新の研究では低分子触媒反応の反応機構解析に留まらず,指向性進化法によって最適化した酵素をQM/MMレベルによってモデル化し,遷移状態計算などを行うことで変異したアミノ酸が反応性・選択性向上に果たす役割を考察するなどの研究も行われています.
今回の記事では,
- 遷移状態とは何か
- Psi4を用いてどのように遷移状態を求めていくか
- 遷移状態の初期構造を求めるテクニック
- 得られた虚振動の可視化
などについて触れていきたいと思います.

遷移状態とは
有機化学を学んだ方なら,以下のような反応エネルギー図を見たことがあると思います.原系である基質が遷移状態を経て生成系である目的物へと変換される過程を示しています.この図では縦軸はエネルギー,横軸は「反応座標」と呼ばれる反応の進行度を示す指標を意味しています.
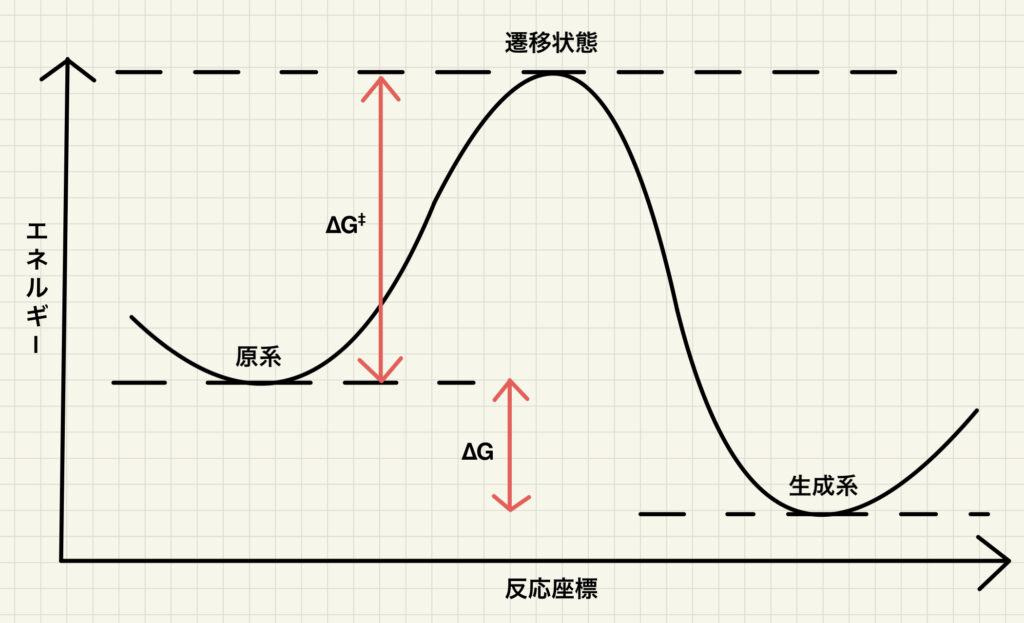
この図からわかるように,遷移状態とは原系と生成系を繋ぐ経路上におけるエネルギーの極大値です.より厳密には,「反応座標」で表される振動モードに対応する極大値で,かつ他の全ての振動モードにおける極小値が遷移状態となります.
基本的には極小値(安定構造)でありながら,ある振動モードに沿ってのみ極大値であることが遷移状態の特徴です.この特徴のため,単純にエネルギーが下がる方向に原子を動かす構造最適化と比べて遷移状態の最適化は難しくなっています.通常は遷移状態に近い構造を初期構造に与えて計算を開始しないと,遷移状態を求めることはできません.もちろん効率的な遷移状態探索のための様々なアルゴリズムが考案されていますが,全ての遷移状態に適用可能な方法はありません.
計算化学の観点からは最適化した構造に対して振動数計算を行うことで,
- 全ての振動数が正であれば安定構造
- 負の振動数(または虚数)を1つのみ持てば遷移状態
- 複数の負の振動数がある場合は高次の按点(不安定構造)
と最適化構造の性質を判断することができます.
Psi4を用いた遷移状態の最適化
今回の計算も以下の条件・環境にて,「.py」ファイルをターミナル上動作させました.手許の計算機で動かす場合には,適宜メモリやスレッド数などの設定項目を変更して下さい.
from __future__ import annotations
import sys
import time
import pathlib
import numpy as np
import psi4
print(f'python version:\n{sys.version}')
# python version:
# 3.9.7 (default, Sep 16 2021, 13:09:58)
# [GCC 7.5.0]
print(f'numpy version:\t{np.__version__}')
# numpy version: 1.21.4
print(f'psi4 version:\t{psi4.__version__}')
# psi4 version: 1.4.1
filename = pathlib.Path(__file__)
logfile = filename.with_suffix('.log').name
psi4.set_output_file(logfile)
psi4.set_memory('14GB')
psi4.set_num_threads(10)
基本的な遷移状態の構造最適化
psi4.optimize(level-of-theory, molecule)
psi4.frequency(level-of-theory, molecule)
Psi4における遷移状態の構造最適化はopt_typeオプションでtsを設定し,通常と同じように構造最適化を行うだけです.また正確なHessianを使って最適化した方が成功率が上がりますので,full_hess_everyオプションも設定しておいた方が無難です(0は計算開始時にHessianを計算).最適化が終わったら,同じ計算レベルで振動数計算を行い,虚振動が1つのみであることを確認します.
以下の例ではエタンの炭素ー炭素結合の回転に関する遷移状態を求めます.我々はgauche型(anti型)が安定配座であり,eclipsed型の配座が遷移状態であることを知っていますので,二面角を0に設定した初期構造から最適化を開始しています.計算レベルはB3LYP/6-31G(d)としています.
# ethane_ts.py
ethane: psi4.core.Molecule = psi4.geometry('''
0 1
C -0.95734121 0.18849206 0.00000000
H -0.60068678 -0.82031794 0.00000000
H -0.60066837 0.69289025 -0.87365150
H -2.02734121 0.18850524 0.00000000
C -0.44399899 0.91444833 1.25740497
H -1.27619066 1.24417191 1.84361261
H 0.15659956 0.24411052 1.83604872
H 0.14426684 1.75946059 0.96620469
''')
psi4.set_options({'opt_type': 'ts',
'full_hess_every': 0})
level = 'b3lyp/6-31g(d)'
wfn: psi4.core.Wavefunction
_, wfn = psi4.optimize(level, molecule=ethane, return_wfn=True)
_, wfn = psi4.frequency(level, molecule=ethane,
ref_gradient=wfn.gradient(),
return_wfn=True)
freqs = np.array(wfn.frequencies())
print(f'optimized structure:\n{ethane.save_string_xyz()}')
print(f'frequency:\n{freqs}')
計算によって得られた構造と振動数の出力結果が以下になります.「-305」という唯一の負の振動数が得られており,遷移状態を求めることができました.
optimized structure: 0 1 C -0.257462213432 -0.364099026624 -0.630640151182 H 0.089253336937 -1.401858131886 -0.671073410689 H 0.083172835766 0.124098924592 -1.549567118633 H -1.351444886940 -0.389566220014 -0.667333253395 C 0.257461683872 0.364095258545 0.630642525139 H -0.565428648413 0.721870058452 1.258051393924 H 0.875397997830 -0.290239328173 1.254173979894 H 0.869055670194 1.235739562893 0.375720142601 frequency: [-305.80692898 910.30603994 910.58322481 1006.89032967 1187.0633733 1187.07613252 1432.1746588 1473.78589517 1533.2435669 1533.25469174 1542.56489807 1542.68371794 3056.65000767 3063.469073 3109.82228746 3109.8570439 3131.22208077 3131.26863144]
遷移状態の初期構造を作成する
遷移状態の最適化は難しいため,計算を始める初期構造(遷移状態の推定構造)が非常に重要になります.初期構造の作成には,化学者の持てる知識を総動員して初期構造を作成していきます.
エタンの炭素–炭素結合の場合はeclipsed型の配座が遷移状態であるという知識を利用しました.それでは,このような自明な初期構造の作成が難しい場合はどうしたらよいでしょうか?
遷移状態の推定構造作成に最もよく使われる手法は,「反応座標」と想定される軸に沿って構造を少しずつ変化させながらエネルギーを調べていく方法になります.その結果,エネルギーが最大の構造が推定遷移状態になります.スキャンする「軸」としては,
- 結合長
- 二面角
などが一般的です.複雑な化学変換の場合は2つ以上の変数を同時にスキャンすることもあります.
例えば上記のエタンの場合では二面角をスキャンしたエネルギー図が我々の頭の中にあり,eclipsed型の配座を推定構造として選んでいるわけです.
以下では2-ピリドンと2-ヒドロキシピリジンの互変異性を例として,その遷移状態を求めていきます.
制限付き最適化によるエネルギースキャン
psi4.set_options({‘optking__opt_coordinates’: ‘both’})
「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事でも説明したように,制限付き最適化はoptkingモジュールのfixed_distanceオプションを用います.またスキャンステップが進んで行くにつれて内部座標を用いた二面角の定義失敗(原子が直線になる等)などの原因でエラーが出ることが多いため,opt_coordinatesオプションで内部座標に加えてデカルト座標も用いるbothを設定しておきます.
なお以前はモジュールオプションの設定にはset_module_optionsというメソッドを使っていましたが,この書き方はver 1.5より非推奨になるようです.代わりに,module-name__option-nameというモジュール名の後に「__」(アンダースコア2つ)をつけた方法が推奨されています.
下記に原子1と原子2の距離を1.5オングストロームに設定したい場合を具体例として示します.
psi4.set_module_options(‘optking’, {‘fixed_distance’: ‘1 2 1.5})
・ver 1.5から
psi4.set_options({‘optking__fixed_distance’: ‘1 2 1.5})
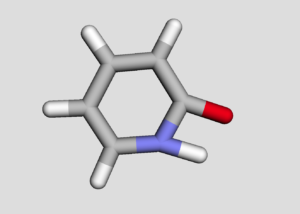
2-ピリドンの互変異性
N–H結合長に沿った構造のスキャン
今回は2-ヒドロキシピリジンを初期構造として,N–H結合の長さを変えていきます.初期構造ではN–Hの長さは2.5オングストロームで,これを徐々に縮めていき2-ピリドンに近い構造へと変化させていきます.
検索するとアンモニアのN–H結合が1.017オングストロームとわかります.今回は遷移状態を求めたいので,それよりもやや長い1.1までをスキャン範囲とします.素早く終えるために計算レベルはHF/STO-3Gとしています.またstep_limitオプションを用いて構造最適化の際に原子を動かす距離を規定値(0.5)よりも細かく動かすようにしています.
下記コードでは構造最適化が規定回数(今回は200回)で終わらなかった場合は,OptimizationConvergenceErrorが出ますのでそれをキャッチしてHessianを毎回計算しながら再び構造最適化を行っています.構造スキャンの各ステップでエネルギーと最適化構造をリストに保存し,最後に最大のエネルギーを与えるN–H結合長とその時の構造を出力しています.ここで得られる構造が,推定遷移状態になります.
# pyridone_01.py
# input structure: 11 12 2.50
mol: psi4.core.Molecule = psi4.geometry('''
0 1
C -1.18551580 1.06150792 0.00000000
C 0.90718220 2.26925892 0.00000000
C 0.20952820 3.47776792 -0.00119900
C -1.18529680 3.47768992 -0.00167800
C -1.88289780 2.26948392 -0.00068200
H -1.73527480 0.10919092 0.00045000
H 0.75972820 4.42991092 -0.00125800
H -1.73541880 4.42997092 -0.00263100
H -2.98250180 2.26966692 -0.00086200
O 2.33718196 2.26936295 0.00082444
H 2.65791173 1.44507402 -0.37237814
N 0.20964420 1.06150792 0.00000000
''')
scan_range = np.linspace(2.5, 1.1, 20)
level = 'hf/sto-3g'
energies = []
structures = []
for dist in scan_range:
psi4.set_options({'geom_maxiter': 200,
'full_hess_every': 0,
'optking__fixed_distance': f'11 12 {dist}',
'optking__opt_coordinates': 'both',
'optking__interfrag_step_limit': 0.3,
'optking__intrafrag_step_limit': 0.3
})
print('-----')
print(f'optimization at {dist:.2f}')
start = time.time()
# 最適化に失敗したらやり直す
try:
energy = psi4.optimize(level, molecule=mol)
except psi4.driver.p4util.exceptions.OptimizationConvergenceError as err:
print(err)
psi4.set_options({'full_hess_every': 1})
energy = psi4.optimize(level, molecule=mol)
end = time.time()
print(f'It took {(end - start)/60:.2f} min for the optimization.')
print(f'energy: {energy:.4f} a.u.')
print(f'optimized structure:\n{mol.save_string_xyz()}')
energies.append(energy)
structures.append(mol.save_string_xyz())
energies = np.array(energies)
print(energies)
# エネルギーが最大となる構造を取得
max_id = np.argmax(energies)
print(f'energy is maximized at {scan_range[max_id]:.2f} A.')
print(f'structure:\n{structures[max_id]}')
with open('pyridone_ts.xyz', 'w') as f:
print(mol.natom(), file=f)
print(structures[max_id], file=f)
この条件では1.17Åでエネルギーが最大となりました.
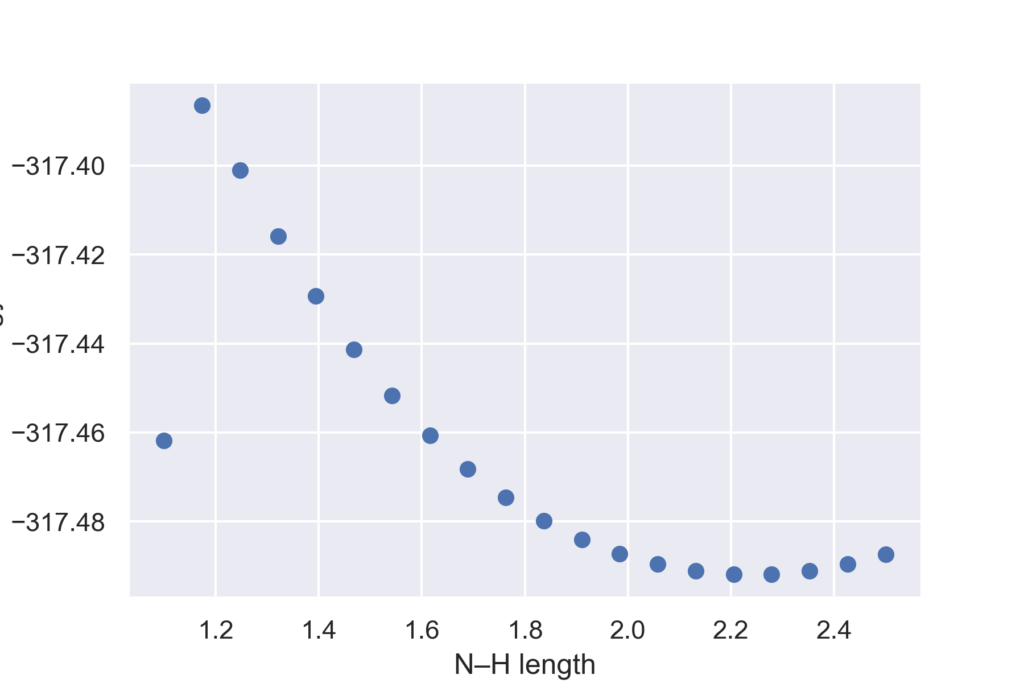
遷移状態の最適化
続いて得られた構造を初期構造として遷移状態を求めていきます.こちらのコードはエタンの場合とほぼ同じで,
- 構造最適化に先立ってHessianを計算(’full_hess_every’: 0)
- 最適化
- 同じ計算レベル(HF/STO-3G)で振動数計算
を行います.
# pyridone_02.py
mol: psi4.core.Molecule = psi4.geometry('''
0 1
C -1.056960044037 -1.155177786154 0.000002997701
C 0.926839264341 0.149760758277 -0.000002625378
C 0.203253130692 1.363564101170 -0.000000557919
C -1.161732028754 1.246258982927 0.000002883772
C -1.812565653014 -0.009198517163 0.000004868201
H -1.503686934857 -2.147387618353 0.000004504304
H 0.704597567951 2.318859721399 -0.000002429518
H -1.771604039138 2.145041594663 0.000004168622
H -2.889693242476 -0.063239313087 0.000007673281
O 2.166792096520 -0.318455056489 -0.000006234219
H 1.454104273468 -1.301458349330 -0.000004168382
N 0.299502884116 -1.071771316189 -0.000000064652
''')
level = 'hf/sto-3g'
psi4.set_options({'geom_maxiter': 100,
'opt_type': 'ts',
'full_hess_every': 0})
wfn: psi4.core.Wavefunction
_, wfn = psi4.optimize(level, molecule=mol, return_wfn=True)
_, wfn = psi4.frequency(level, molecule=mol,
ref_gradient=wfn.gradient(),
return_wfn=True)
print(f'optimized structure:\n{mol.save_string_xyz()}')
print(f'frequency:\n{np.array(wfn.frequencies())}')
最適化後の構造と振動数は以下の通りでした.用いた推定遷移状態が適切だったためか,今回も「-2496」という唯一の負の振動数が得られています.
optimized structure: 0 1 C -1.073986885437 -1.170578359942 0.000002755738 C 0.953021017198 0.140745143377 -0.000003061297 C 0.196029366481 1.360797354321 -0.000001202096 C -1.155622586106 1.236381947214 0.000002880952 C -1.818434996700 -0.031125507024 0.000005467599 H -1.510894241728 -2.166796480067 0.000004269828 H 0.691726656323 2.319296967258 -0.000002742435 H -1.770734621411 2.131633416218 0.000004678262 H -2.895472126141 -0.076640107909 0.000009377672 O 2.177846935050 -0.264655641303 -0.000003962413 H 1.432324292904 -1.412270186206 -0.000002894660 N 0.288380859812 -1.071403950594 -0.000002249524 frequency: [-2496.96943661 194.43320886 438.12377096 536.77066379 544.82299481 674.62986545 770.64975411 823.30045251 883.85855328 988.33843048 993.62719504 1130.2547344 1151.3865942 1158.50875496 1202.89831356 1324.40587325 1340.95261351 1409.33317838 1471.43172362 1482.05854529 1615.05493361 1717.80892579 1798.69689446 1872.67207468 1974.87690229 2810.69765603 3708.9263432 3715.47092791 3755.16051734 3759.94780592]
振動モードの可視化
前述のように負の振動数(虚振動)の数を調べれば最適化構造の性質を知ることができます.しかし得られた構造が遷移状態だったとしても望みの原系と生成系を繋ぐ遷移状態であるとは限りません.
振動数計算では「対象となる基準振動ではどの原子がどの方向に動くか」に関する情報も出力されます.得られた虚振動についてこの情報を調べることで,望みの振動モードに対応する遷移状態かどうかを判断することができます.
今回の場合ですとログファイルには以下のように出力されています.1番目の「2496.9694i」が調べたい虚の振動数です.特に11番目の原子である水素が大きく動くことがわかりますので,この水素の移動に関する望みの振動モードであると判断できます.
・・・略・・・
Vibration 1 8 9
Freq [cm^-1] 2496.9694i 194.4332 438.1238
Irrep A A A
Reduced mass [u] 1.1191 7.2827 3.4977
Force const [mDyne/A] -4.1110 0.1622 0.3956
Turning point v=0 [a0] 0.0000 0.2916 0.2803
RMS dev v=0 [a0 u^1/2] 0.0000 0.5564 0.3707
IR activ [km/mol] 183.0435 0.0542 2.7477
Char temp [K] 0.0000 279.7461 630.3626
----------------------------------------------------------------------------------
1 C 0.01 0.01 -0.00 -0.00 -0.00 -0.01 -0.00 -0.00 -0.22
2 C -0.07 0.01 0.00 0.00 0.00 0.15 -0.00 -0.00 -0.07
3 C 0.02 -0.01 -0.00 0.00 -0.00 0.25 -0.00 -0.00 -0.23
4 C -0.02 -0.01 0.00 -0.00 -0.00 -0.05 0.00 0.00 0.23
5 C -0.00 0.02 0.00 -0.00 0.00 -0.28 0.00 0.00 0.02
6 H 0.01 0.01 -0.00 -0.00 -0.00 -0.09 -0.00 -0.00 -0.55
7 H 0.00 -0.00 0.00 0.00 -0.00 0.33 -0.00 -0.00 -0.43
8 H 0.00 -0.00 0.00 -0.00 -0.00 -0.15 0.00 0.00 0.48
9 H -0.01 0.01 0.00 -0.00 0.00 -0.60 -0.00 0.00 -0.10
10 O 0.01 -0.05 0.00 0.00 -0.00 -0.38 0.00 0.00 0.03
11 H 0.84 0.53 -0.00 0.00 -0.00 -0.09 0.00 -0.00 0.24
12 N -0.02 0.00 0.00 0.00 0.00 0.42 0.00 -0.00 0.23
・・・略・・・
molden形式のファイルを可視化
Psi4ではnormal_modes_writeオプションを設定することで,molden形式という振動モードに関する情報を含んだファイルを出力できます.このファイル形式はmolden以外の可視化ソフトでも読み込み可能です.
Avogadro
Psi4で出力したファイルの拡張子は「.molden_normal_modes」となっています.このままではAvogadroでは認識されないため,拡張子を「.molden」へと変更します.ファイルを読み込むと下記のように,振動数のリストが表示されます.アニメーションさせたい振動数を選んで,下の「Start Animation」ボタンを押すことで振動モードの可視化が可能です.

py3Dmol
「py3Dmolを使って化学構造をJupyter上で美しく表示する」という記事で解説した3Dmol.jsをJupyterノートブック上で動かすウィジェットによる可視化も可能です.GitHubのnormal-mode-jupyterというコードを利用します.
helpers.show_normal_modesという関数を用います.この場合は拡張子は「.molden_normal_modes」のままで大丈夫です.インストールは例えばGoogle Colab上では下記のように行います.
!pip install py3Dmol
import py3Dmol
!git clone https://github.com/duerrsimon/normal-mode-jupyter.git
sys.path.append('/content/normal-mode-jupyter')
from helpers import show_normal_modes
molden形式のファイルを読み込むと以下のように,振動モードをプルダウンで選択しながらアニメーションさせられます.
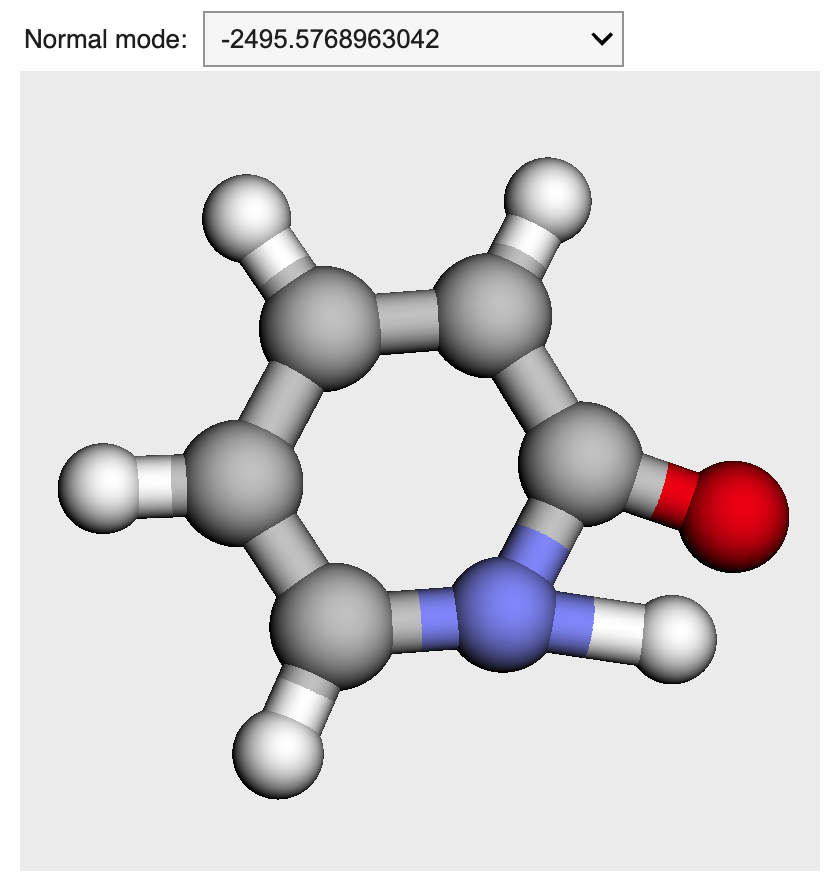
複数構造を含むxyzファイルによるアニメーション
「XYZ形式とZ-マトリックスは分子の立体構造を表す入力フォーマット」という記事でも述べたように,XYZ形式のファイルには複数の構造を入力することが可能です.ファオーマットは以下のように次々とXYZ形式のブロックを重ねるだけです.
1つめの原子数 1つめのコメント 元素記号 x座標 y座標 z座標 元素記号 x座標 y座標 z座標 ・・・ 2つめの原子数 2つめのコメント 元素記号 x座標 y座標 z座標 元素記号 x座標 y座標 z座標 ・・・ 3つめの原子数 3つめのコメント ・・・
このような複数の構造を含んだファイルをVMDやPyMOLで読み込むことで,複数の構造がセットになった構造が読み込まれます.これらソフト上で構造を切り替えていくとアニメーションが作成可能です.
先ほどの振動モードに関する移動差分(delta)を用いて,
- 遷移状態を正の方向に動かした構造
- 遷移状態
- 遷移状態を負の方向に動かした構造
- 遷移状態
の4つの構造を入力したxyzファイルを作成してみます.この構造をループさせると遷移状態から正負の方向に振動する様子がアニメーションとして再生されます.
12 0 1 C -1.063989066950 -1.160580739498 0.000002755744 C 0.883022827673 0.150745452453 -0.000003061303 C 0.216029809410 1.350800123887 -0.000001202098 C -1.175624996508 1.226384461689 0.000002880958 C -1.818438725073 -0.011125529835 0.000005467610 H -1.500897319041 -2.156800902189 0.000004269837 H 0.691728074583 2.319301722558 -0.000002742441 H -1.770738251983 2.131637786748 0.000004678272 H -2.905478083287 -0.066640244542 0.000009377691 O 2.187851420835 -0.314656286447 -0.000003962421 H 2.272328951895 -0.882271995142 -0.000002894666 N 0.268381410078 -1.071406147314 -0.000002249529 12 0 1 C -1.073986885437 -1.170578359942 0.000002755738 C 0.953021017198 0.140745143377 -0.000003061297 C 0.196029366481 1.360797354321 -0.000001202096 C -1.155622586106 1.236381947214 0.000002880952 C -1.818434996700 -0.031125507024 0.000005467599 H -1.510894241728 -2.166796480067 0.000004269828 H 0.691726656323 2.319296967258 -0.000002742435 H -1.770734621411 2.131633416218 0.000004678262 H -2.895472126141 -0.076640107909 0.000009377672 O 2.177846935050 -0.264655641303 -0.000003962413 H 1.432324292904 -1.412270186206 -0.000002894660 N 0.288380859812 -1.071403950594 -0.000002249524 12 0 1 C -1.083989107956 -1.180580780505 0.000002755744 C 1.023023114718 0.130745411446 -0.000003061303 C 0.176029727397 1.370800164894 -0.000001202098 C -1.135624914495 1.246384502695 0.000002880958 C -1.818438725073 -0.051125611847 0.000005467610 H -1.520897360047 -2.176800943195 0.000004269837 H 0.691728074583 2.319301722558 -0.000002742441 H -1.770738251983 2.131637786748 0.000004678272 H -2.885478042281 -0.086640285549 0.000009377691 O 2.167851379829 -0.214656081415 -0.000003962421 H 0.592325507358 -1.942274168480 -0.000002894666 N 0.308381492091 -1.071406147314 -0.000002249529 12 0 1 C -1.073986885437 -1.170578359942 0.000002755738 C 0.953021017198 0.140745143377 -0.000003061297 C 0.196029366481 1.360797354321 -0.000001202096 C -1.155622586106 1.236381947214 0.000002880952 C -1.818434996700 -0.031125507024 0.000005467599 H -1.510894241728 -2.166796480067 0.000004269828 H 0.691726656323 2.319296967258 -0.000002742435 H -1.770734621411 2.131633416218 0.000004678262 H -2.895472126141 -0.076640107909 0.000009377672 O 2.177846935050 -0.264655641303 -0.000003962413 H 1.432324292904 -1.412270186206 -0.000002894660 N 0.288380859812 -1.071403950594 -0.000002249524
静止画ですが,VMDで読み込んだ図は以下のようになりました.
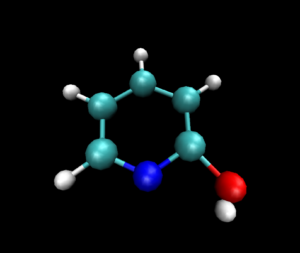
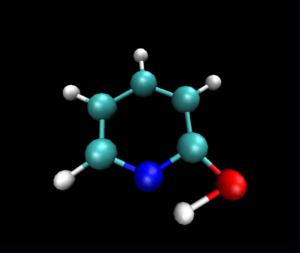
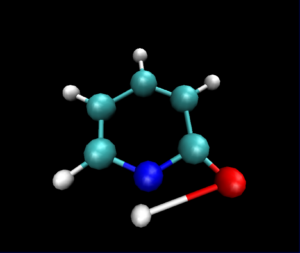
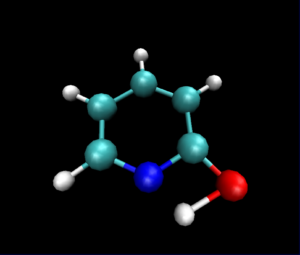
py3Dmolを使った可視化
view.animate({‘loop’: ‘backAndForth’})
py3Dmol自体の機能を用いても振動モードの可視化が可能です.その場合はviewオブジェクトに分子を追加する際にvibrateオプションを設定します.アニメーションの1周期がデフォルト設定で10フレームです.
またpy3Dmolで可視化する場合にはXYZファイルのフォーマットが異なり,下記のようにXYZの各座標に続いて,それぞれの原子の移動差分を追記していきます.
原子数 コメント 元素記号 x座標 y座標 z座標 x座標の差分 y座標の差分 z座標の差分 元素記号 x座標 y座標 z座標 x座標の差分 y座標の差分 z座標の差分 ・・・
今回の例ですと以下のようなファイルを作成します.
12 for a visualization on py3Dmol C -1.0739868854371193 -1.1705783599418247 2.7557380046401337e-06 0.01 0.01 -0.0 C 0.9530210171978807 0.14074514337717564 -3.061296995359866e-06 -0.07 0.01 0.0 C 0.1960293664808807 1.3607973543211755 -1.2020959953598667e-06 0.02 -0.01 -0.0 C -1.1556225861061196 1.2363819472141755 2.8809520046401337e-06 -0.02 -0.01 0.0 C -1.8184349967001192 -0.03112550702382436 5.4675990046401335e-06 -0.0 0.02 0.0 H -1.5108942417281193 -2.1667964800668242 4.269828004640134e-06 0.01 0.01 -0.0 H 0.6917266563228808 2.319296967258176 -2.742434995359867e-06 0.0 -0.0 0.0 H -1.7707346214111193 2.131633416218176 4.678262004640133e-06 0.0 -0.0 0.0 H -2.895472126141119 -0.07664010790882435 9.377672004640133e-06 -0.01 0.01 0.0 O 2.1778469350498804 -0.2646556413028243 -3.962412995359866e-06 0.01 -0.05 0.0 H 1.4323242929038806 -1.4122701862058247 -2.894659995359867e-06 0.84 0.53 -0.0 N 0.2883808598118807 -1.0714039505938244 -2.2495239953598667e-06 -0.02 0.0 0.0
このファイルを用いてJupyterノートブック上でアニメーションを行ってみます.
import py3Dmol
with open('py3dmol.xyz', 'r') as f:
file = f.read()
view = py3Dmol.view(width=680, height=480)
view.addModel(file, 'xyz', {'vibrate': {'frames': 10, 'amplitude':1}})
view.setStyle({'stick': {}})
view.animate({'loop': 'backAndForth'})
view.setBackgroundColor('#e1e1e1')
view.show()
こちらも静止画ですがpy3Dmolで可視化したものが以下のようです.
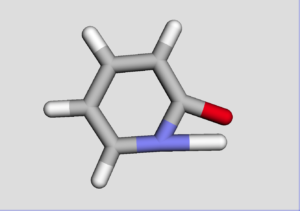
終わりに
今回は「Psi4で遷移状態最適化:計算化学における虚振動と化学構造」という話題について,
- 遷移状態とは何か
- Psi4を用いてどのように遷移状態を求めていくか
- 遷移状態の初期構造を求めるテクニック
- 得られた虚振動の可視化
などについて説明しました.
遷移状態最適化は通常の構造最適化と異なり,闇雲に初期構造を与えるだけでは望みの構造にたどり着くことはほとんど期待できません.対象とする反応系に関する化学知識を動員しながら,きちんと初期構造を作成することが大切です.基本的な反応について遷移状態の最適化ができるようになれば,初心者を脱出したと言っても差し支えないかもしれません.
今回は得られた遷移状態構造について負の振動数に関する基準振動を可視化するとことで,望みの構造を繋ぐ遷移状態であることを確認しました.多くの場合,このような目視による確認で望みの遷移状態か否かを調べることができます.
次回はより厳密な方法として,固有反応座標(IRC)を求めることで,得られた構造が確かに所望の原料と生成物を繋ぐ遷移状態であることを確認していきます.反応機構に関する計算の論文では必ず「IRC計算による確認を行った」旨の記述があるように,IRC計算は遷移状態を求めたら必ず実行しなければならない計算です.次回はPsi4を使ったIRC計算について見ていきたいと思います.
>>次の記事:「Psi4でIRC計算:固有反応座標で反応経路を求める」
コメント