前回までに引き続き,ハンバーガー統計学をもとにした分析をpythonで進めることで,基本的な統計学の内容をどのようにpythonで表現していくかを学びます.具体的には今回はscipy.statsとstatsmodelを用いて,
- χ二乗検定
- t検定
- 一元配置分散分析
- 二次元配置分散分析
- 多重比較法
などを扱います.
なお,これまでの記事はこちらです.
– 「pythonで統計学基礎: 01 平均と分散」
– 「pythonで統計学基礎:02 信頼区間・t分布」
ライブラリのインポート
まずは必要なライブラリのimportを行いましょう.
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy import stats import seaborn as sns sns.set()
データのまとめ方
通常データが得られる形は,1行が1件のデータを形成し,各列が変数を成すようなデータが多いです.例えば下の表のような各客がどの店舗で何を買ったかのデータでは,お客ごとに1つの行でデータを形成し,店舗と買ったものが変数になります.
| 客ID | 店舗 | 買い物 |
|---|---|---|
| 001 | わくわく | ポテト |
| 002 | わくわく | ポテト |
| 003 | もぐもぐ | ポテト |
| 004 | もぐもぐ | チキン |
| 005 | わくわく | ポテト |
| 006 | もぐもぐ | チキン |
| 007 | わくわく | チキン |
| 008 | もぐもぐ | ポテト |
| 009 | もぐもぐ | ポテト |
| 010 | わくわく | ポテト |
このようなデータ形式は人間にはわかりにくいですが,コンピュータにとっては理解しやすいデータ形式です.一方で人間が理解しやすいデータはコンピュータには理解しにくい場合が多いので,データ自体はコンピュータに理解しやすい形で保存し,そのデータに処理を施すことで人間がわかりやすい形にすることを心がけましょう.多くの場合,人に扱いやすい形にする過程で生データに含まれる情報の一部が失われてしまいますし,人間が見やすいデータをコンピュータで扱いやすいデータに戻すのは手間がかかります.
χ二乗検定
2つのお店の売り上げデータをpandasのデータフレームとして入力し(赤字部分),得られたテーブルをscipy.stats.chi2_contingencyで処理することで,χ二乗検定が行えます.
「contigency table」とは聞き慣れない単語かもしれませんが「分割表」のことで,下のようなテーブルを指します.前述の人間が理解しやすいデータ形式の1つです.つまり分割表を入力データとすることでχ二乗検定を行ってくれるメソッドになります.
| potato | chicken | total | |
|---|---|---|---|
| wakuwaku | 435 | 165 | 600 |
| mogumogu | 265 | 135 | 400 |
| total | 700 | 300 | 1000 |
下のコードでは分割表を手入力していますが,多くの場合は生データを加工して分割表を作成するステップが必要です.
df1 = pd.DataFrame({'potato': [435, 265], 'chicken': [165, 135]},
index=['wakuwaku', 'mogumogu'])
stats.chi2_contingency(df1, correction=False)
(4.464285714285714, 0.03461055751570723, 1,
array([[180., 420.],
[120., 280.]]))
戻り値はχ二乗値,p値,帰無仮説下での売り上げデータです.すなわち以下のデータを仮定してχ二乗値を求めていることになります.(pandasの都合上データの順番が変わっています)
| chicken | potato | total | |
|---|---|---|---|
| wakuwaku | 180 | 420 | 600 |
| mogumogu | 120 | 280 | 400 |
| total | 300 | 700 | 1000 |
平均値の差の検定:scipyに実装されているいろいろなt検定
平均値の差の検定と言われる,2群間の差があるかないかを調べるt検定には前提条件によって色々なバリエーションが存在し,用いるべきpythonのメソッドも異なります.
t検定用のメソッドはscipy.stats.ttest_XXXXの形で4種類存在しています.
対応なしのt検定
scipy.stats.ttest_ind_from_stats
対応なしのt検定とは,各々の処置をされた被験者間に関係がない場合に用いる検定で,そのうち入力データの形によって
- scipy.stats.ttest_ind
- scipy.stats.ttest_ind_from_stats
の何れかを用いることになります.
生データからのt検定
入力データが各群における生データの場合の例が以下のコードになります.ttest_indは入力データ2つを配列で受け取ります.
taste1 = pd.DataFrame({'wakuwaku': [70,75,70,85,90,70,80,75],
'mogumogu': [85,80,95,70,80,75,80,90]})
waku_taste = taste1['wakuwaku']
mogu_taste = taste1['mogumogu']
stats.ttest_ind(waku_taste,mogu_taste)
戻り値はt値とp値になります.今回の場合はp値が0.21と非常に大きいので帰無仮説が棄却できません.
Ttest_indResult(statistic=-1.2881223774390613, pvalue=0.21858702220219914)
データの平均と標準偏差からのt検定
ttest_indではt検定を行うにあたり,データの配列を入力値としました.もしデータの平均値,標準偏差,データ数のみがわかっている場合にはscipy.stats.ttest_ind_from_statsを使うことでt検定が行えます.
stats.ttest_ind_from_stats(mean1=waku_taste.mean(),
std1=waku_taste.std(),
nobs1=len(waku_taste),
mean2=mogu_taste.mean(),
std2=mogu_taste.std(),
nobs2=len(mogu_taste))
今回の場合は元データが同じですので,結果は当然同じになります.
Ttest_indResult(statistic=-1.2881223774390613, pvalue=0.21858702220219914)
対応ありのt検定
scipy.stats.ttest_rel(list1, list2)
対応ありのt検定とは,異なる処置を同じ個体に施す場合などに使います.この場合は個体差が無視できるようになるため,全体の差の標準誤差が小さくなります.そのため信頼区間が狭くなり,類似のデータを用いた場合にも検出力の高い検定が可能になります.
対応ありt検定はscipyではscipy.stats.ttest_1sampまたはscipy.stats.ttest_relに実装されています.前者は2つの群の差を引数に与えるのに対し,後者では2つの群のデータをリストで渡します.
waku_taste2 = pd.Series([90,75,75,75,80,65,75,80]) mogu_taste2 = pd.Series([95,80,80,80,75,75,80,85]) stats.ttest_rel(waku_taste2,mogu_taste2)
戻り値は対応なしと同様に,t値とp値です.この場合には5%水準で棄却できる結果になりました.
Ttest_relResult(statistic=-2.965614910077132, pvalue=0.020937570206924612)
分散分析
平均値の差の検定においても,比較する系が3つ以上の場合には検定の多重性のためにt検定を使うことはできません.このような場合にも使える分析手法として,分散の比を考える分散分析(ANOVA)があります.
pythonでは
- 変数が1つの一元配置分散分析はscipy.stats.f_onewayやstatsmodels
- 二次元配置分散分析はstatsmodels
に実装されています.これから見ていくように,statsmodelsにおける実装はともに正規線形モデルの枠組みで取り扱います.
scipy.statsによる一元配置分散分析(One-way ANOVA)
一次元配置分散分析の分析を行う,f_onewayの使い方はほぼ平均値の差の検定で用いたt検定のメソッドと同じで,単純にデータの配列を入力するだけです.
waku_taste3 = pd.Series([80,75,80,90,95,80,80,85,85,80,
90,80,75,90,85,85,90,90,85,80])
mogu_taste3 = pd.Series([75,70,80,85,90,75,85,80,80,75,
80,75,70,85,80,75,80,80,90,80])
paku_taste3 = pd.Series([80,80,80,90,95,85,95,90,85,90,
95,85,98,95,85,85,90,90,85,85])
stats.f_oneway(waku_taste3,mogu_taste3,paku_taste3)
結果の戻り値はF値とp値になります.今回はp値が非常に小さいことから,3つの群のうち少なくともどれかの組み合わせでは差があることがわかります.しかし,どの組み合わせに差があるかがわからないのが,分散分析の弱みで,多重比較法などの他の分析法に頼ることになります.後ほどstatsmodelsに実装されているテューキーの検定法を見てみます.
F_onewayResult(statistic=12.223110194494566, pvalue=3.824826458393889e-05)
stasmodelsを用いた一次元配置の分散分析
statsmodelsを用いたモデル化ではお店の種類という要因によりスコアがどのように変わるかを定式化しようと試みます.
$$ スコア = \beta_{0} + \beta_{1} \times ワクワク + \beta_{2} \times モグモグ + \beta_{3} \times パクパク $$
という式における各係数を求めようとします.実際には,ワクワクでもモグモグでもなければパクパクに一意に定まりますので,上式中のパクパクの係数は不要です.そこでstatsmodelsのデフォルト設定では,カテゴリの1つを定数項に含めて係数の推定を行います.
# 分析用にstasmodelsをimport
import statsmodels.formula.api as smf
import statsmodels.api as sm
# statsmodelsではpandas DataFrameを引数に取るのでデータを集約
shops = ['waku' for _ in range(20)] + ['mogu' for _ in range(20)] + ['paku' for _ in range(20)]
df2 = pd.DataFrame({'shops': shops, 'score': pd.concat([waku_taste3, mogu_taste3, paku_taste3])})
# モデル化
anova = smf.ols('score ~ shops', data = df2).fit()
print(sm.stats.anova_lm(anova, typ=2))
print(anova.params)
分散分析表に表示されているp値は先ほどscipyを用いた値と同じになっています.
| sum_sq | df | F | PR(>F) | |
|---|---|---|---|---|
| shops | 748.633333 | 2.0 | 12.22311 | 0.000038 |
| Residual | 1745.550000 | 57.0 | NaN | NaN |
また各係数は下記のようになりました.先ほど述べたように店舗がモグモグを基本ライン(定数項に合併された)として,パクパクだと8.65,ワクワクだと4.50の加点が得られるようなモデルが作成されたとわかります.この辺りは次回以降に線形モデルを見ていく際に,詳しく解説していきます.
Intercept 79.50 shops[T.paku] 8.65 shops[T.waku] 4.50
statsmodelsによる多重比較法
ハンバーガー統計学では言及だけで解説されていない「多重比較法」ですが,ここではpythonのstatsmodelsに実装されているテューキーの検定法について簡単に使い方を見ていきます.pairwise_tukeyhsdは第1引数にデータのリスト,第2引数にカテゴリーのリストを取ります.以下のコードで確認してみましょう.
print(pairwise_tukeyhsd(df2.score, df2.shops))
Multiple Comparison of Means - Tukey HSD,FWER=0.05 ============================================= group1 group2 meandiff lower upper reject --------------------------------------------- mogu paku 8.65 4.4389 12.8611 True mogu waku 4.5 0.2889 8.7111 True paku waku -4.15 -8.3611 0.0611 False ---------------------------------------------
2つの店舗間の全ての組み合わせで検定が行われ,結果が表示されました.今回の場合は,「モグモグとパクパクの間」と「モグモグとワクワクの間」に5%の有意水準で差があると言えるようです.
stasmodelsを用いた二次元配置分散分析
statsmodelsを用いると二次元配置の分散分析も同様の手法で行うことが可能です.
データの準備
まずはハンバーガー統計学にあるデータで,
- 味付けが「普通」と「辛口」の2種類
- 食感が「普通」と「クリスピー」の2種類
の計4種類のチキンを15人ずつに食べて貰って評価された点数を入力します.
taste = 2*(['chili' for _ in range(15)] + ['normal' for _ in range(15)])
coating = ['crisp' for _ in range(30)] + ['normal' for _ in range(30)]
df3 = pd.DataFrame({'taste': taste, 'coating': coating,
'score': [65,85,75,85,75,80,90,75,85,65,75,85,80,85,90,
65,70,80,75,70,60,65,70,85,60,65,75,70,80,75,
70,65,85,80,75,65,75,60,85,65,75,70,65,80,75,
70,70,85,80,65,75,65,85,80,60,70,75,70,80,85]})
df3.groupby(['coating', 'taste']).describe().round(2)
各水準毎のデータをまとめたものが下の表になります.
| count | mean | std | min | 25% | 50% | 75% | max | ||
|---|---|---|---|---|---|---|---|---|---|
| coating | taste | ||||||||
| crisp | chili | 15.0 | 79.67 | 7.90 | 65.0 | 75.0 | 80.0 | 85.0 | 90.0 |
| normal | 15.0 | 71.00 | 7.37 | 60.0 | 65.0 | 70.0 | 75.0 | 85.0 | |
| normal | chili | 15.0 | 72.67 | 7.76 | 60.0 | 65.0 | 75.0 | 77.5 | 85.0 |
| normal | 15.0 | 74.33 | 7.99 | 60.0 | 70.0 | 75.0 | 80.0 | 85.0 |
交互作用
今回のように目的値が2つの要因によって変化する場合,
- 要因1(味付け)による効果
- 要因2(食感)による効果
に加えて,
- 要因1と要因2が合わさった効果(交互作用)
を考慮する必要があります.通常は交互作用があるかないかは要因毎にグラフを書いてみるとわかります.statsmodelsにあるinteraction_plotというメソッドを用いると容易に可視化可能です.
from statsmodels.graphics.factorplots import interaction_plot fig = interaction_plot(df3.coating, df3.taste, df3.score, colors=['red', 'blue'], ms=10)
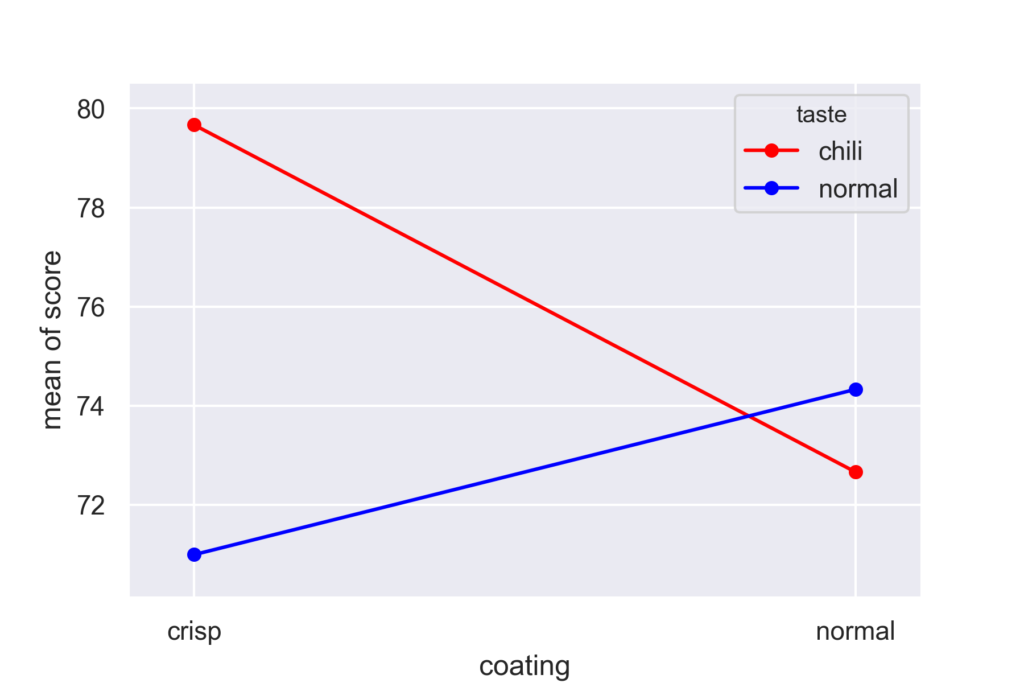
今回の場合は,クリスピー(crisp)な食感は辛口(chili)と合わさると効果的であることがグラフから明らかなので,交互作用がありそうです.
statsmodelsを用いた二次元配置の分散分析
交互作用は2つの要因の「積」としてstatsmodelsのFormulaに入れ込みます.「A : B」または「A * B」のいずれのフォーマットでも認識されます.下のコードでは「*」を用いています.
twoway_anova = smf.ols(formula='score ~ coating + taste + coating*taste', data=df3).fit() sm.stats.anova_lm(twoway_anova, typ=2).round(2)
| sum_sq | df | F | PR(>F) | |
|---|---|---|---|---|
| coating | 50.42 | 1.0 | 0.84 | 0.36 |
| taste | 183.75 | 1.0 | 3.05 | 0.09 |
| coating*taste | 400.42 | 1.0 | 6.65 | 0.01 |
| Residual | 3370.00 | 56.0 | NaN | NaN |
分散分析表によると,
- coating(食感)による違いは有意差なし
- taste(味付け)による違いは有意差なし
- 交互作用による違いは有意差あり
という分析結果になりました.
終わりに
今回は検定と分散分析を内容として,
- 生データのありかた
- 分割表からのχ二乗検定
- 平均値の差の検定:対応なしt検定
- 平均値の差の検定:対応ありt検定
- 平均値の差の検定:一次元配置の分散分析
- statsmodelsによる多重比較法
- statsmodelsによる二次元配置の分散分析
などの内容を扱ってきました.検定で得られたp値が低い場合・高い場合には何が言えるのかなどについても理解を深めていきたいところです.
これまで3回に渡ってハンバーガー統計学の内容を用いてpythonの勉強を進めてきました.複雑な内容も簡単なコードで実現できることがわかってワクワクしてきたかと思います.もちろんプログラムで1発の内容であっても,その中身を理解しないで使うことは誤用の可能性もあり危険です.今後もプログラミング言語の勉強と理論の勉強を常に並行して進めていくことを心がけていきたいですね.
次回からは続編であるアイスクリーム統計学を使って回帰分析などを取り上げる予定です.分散分析の際に用いたstatsmodelsを用いて,分析を進めていきます.
コメント
大変わかりやすかったです