「NumPyのrandomルーチンでいろいろな乱数を生成する」という記事では,numpy.randomに実装されている統計分布からのサンプリングについて扱いました.
統計分布についてにはscipy.statsに一通り確率密度関数から検定までが実装されています.今回はその中から統計分布の扱いについて見ていくことで理解を深めていきたいと思います.
詳細は公式ドキュメントを見て頂きたいのですが,かなりの種類の連続確率変数と離散確率変数が実装されています.chi2のようにnumpy.randomの名前(chisquare)とは異なるものも多々あるので注意が必要です.
基本的な使い方は,
で統一されていて,各確率分布はほぼ共通のメソッドを持っています.そのため,一度使い方を理解してしまえば使い回しが効くのが助かります.ここではいくつかの馴染み深い確率変数についてテーブルにまとめます.まずは連続確率変数についてです.
| 確率分布名 | pythonクラス |
|---|---|
| 正規分布 | stats.norm |
| ベータ分布 | stats.beta |
| χ二乗分布: | stats.chi2 |
| F分布 | stats.f |
| ガンマ分布 | stats.gamma |
| t分布 | stats.t |
| 一様分布 | stat.uniform |
続いて,離散確率変数についてです.
| 確率分布名 | pythonクラス |
|---|---|
| ベルヌーイ分布 | stats.bernoulli |
| 二項分布 | stats.binom |
| ポアソン分布 | stats.poisson |
それでは具体的にpythonのコードを見ていきましょう.まずは必要なライブラリーのimportを行いましょう.
import numpy as np import matplotlib.pyplot as plt import seaborn as sns from scipy import stats x = np.linspace(-5,5,1000) x_discrete = np.arange(-5,5)
確率変数
指定した確率分布に従う変数をsizeだけ返します.numpy.random.XXXと基本的に同じです.下記のコードでは平均50loc=50,標準偏差20scale=20の正規分布から1000サンプルsize=1000取りだしたものを可視化しています.
norm = stats.norm.rvs(loc=50, scale=20, size=1000) sns.distplot(norm, bins=range(0,100))

確率密度関数
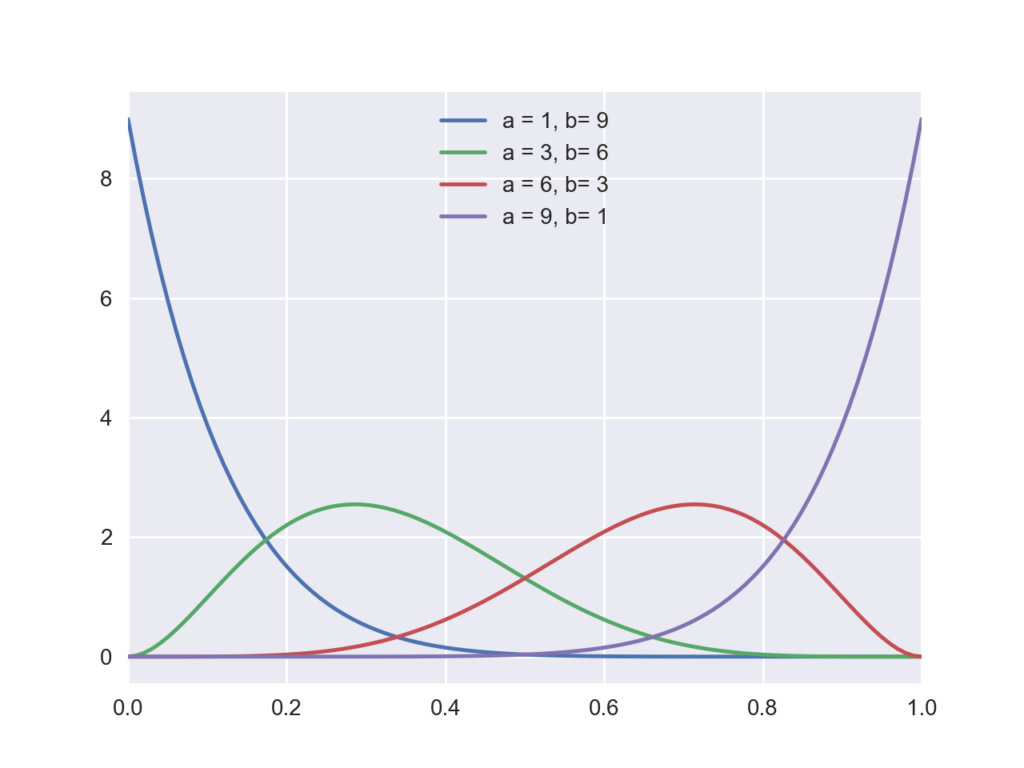
指定した確率分布の確率密度関数を返します.下のコードではaとbを変化させながらベータ分布を描いています.
x = np.linspace(0,1,100)
for a,b in zip([1,3,6,9], [9,6,3,1]):
beta_pdf = stats.beta.pdf(x, a, b)
plt.plot(x,beta_pdf, label='a = {}, b= {}'.format(a,b))
plt.xlim([0,1])
plt.legend(loc='best')
ログ確率密度関数
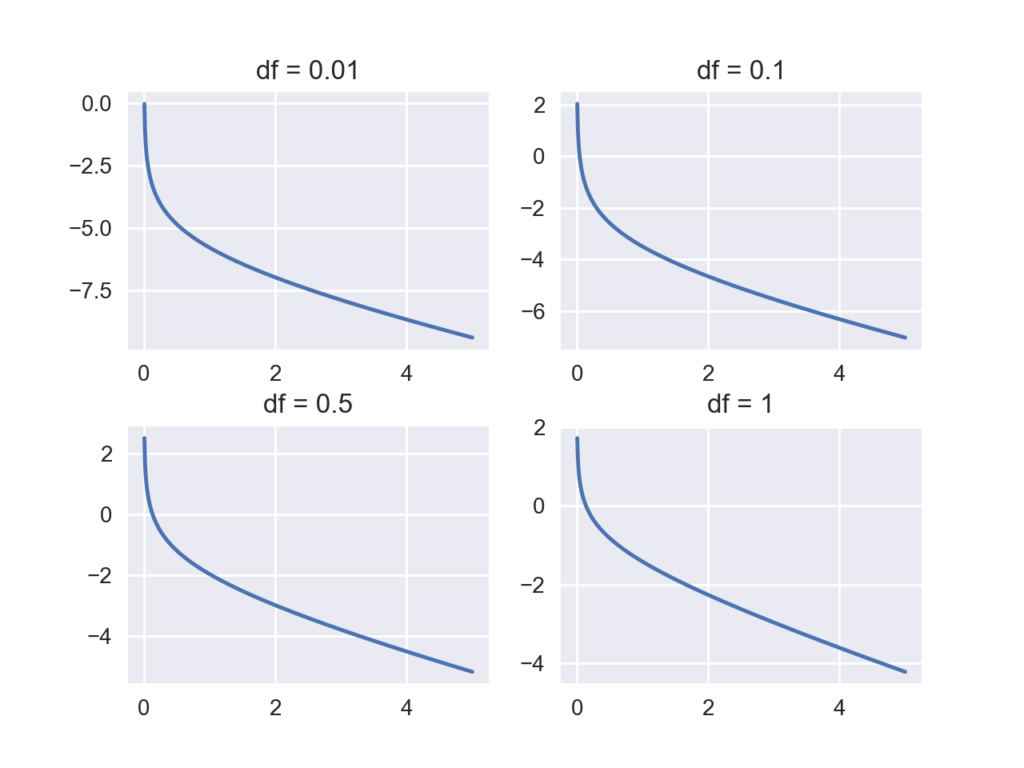
確率密度関数のlogを取ったものを返します.以下の例では自由度を変えてdf=d,χ二乗分布のログ確率密度関数を描画しています.
fig = plt.figure()
dfs = [0.01, 0.1, 0.5, 1 ]
positions = [221,222,223,224]
plt.subplots_adjust(hspace=0.3)
for d, p in zip(dfs, positions):
chi2 = stats.chi2.logpdf(x,df=d)
ax = fig.add_subplot(p)
ax.plot(x,chi2)
ax.set_title('df = {}'.format(d))
確率質量関数
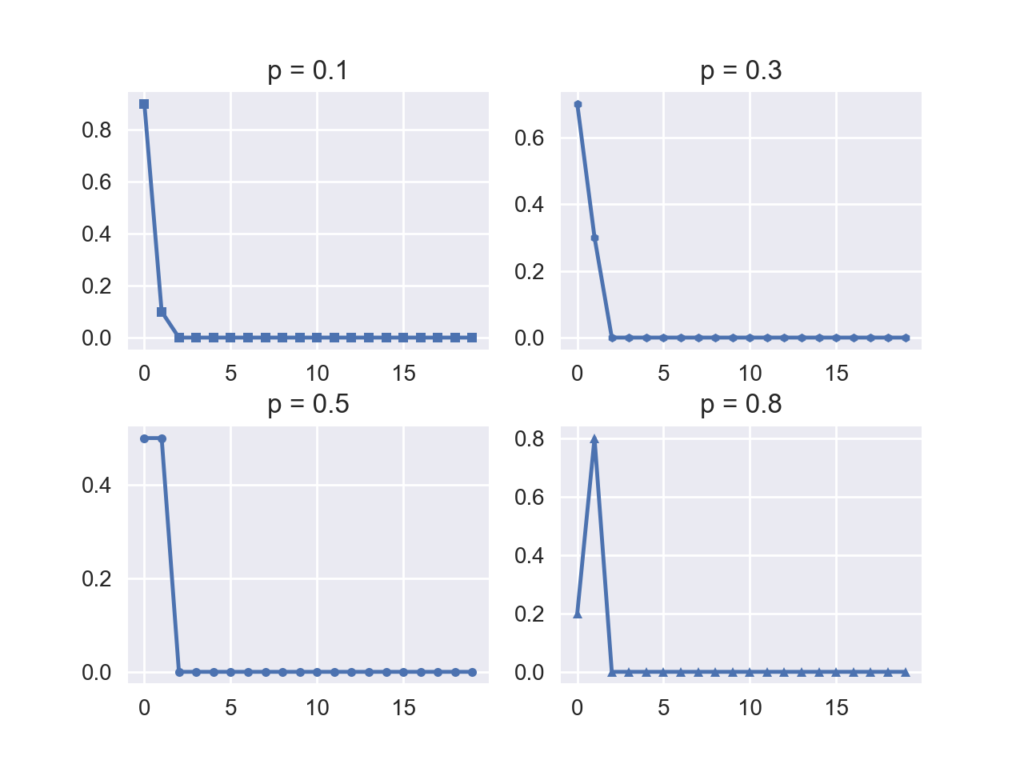
確率分布が離散型の場合は確率質量関数になります.基本的にはpdfと同じです.以下のコードでは生起確率を変えてp=pベルヌーイ分布の確率質量関数を描画しています.
fig = plt.figure()
ps = [0.1, 0.3, 0.5, 0.8]
positions = [221,222,223,224]
markers = ['s', 'h', 'o', '^']
plt.subplots_adjust(hspace=0.3)
for p, s, m in zip(ps, positions, markers):
bernoulli = stats.bernoulli.pmf(x_descrete, p=p)
ax = fig.add_subplot(s)
ax.plot(x_descrete, bernoulli, m+'-', ms=4)
ax.set_title('p = {}'.format(p))
累積分布関数
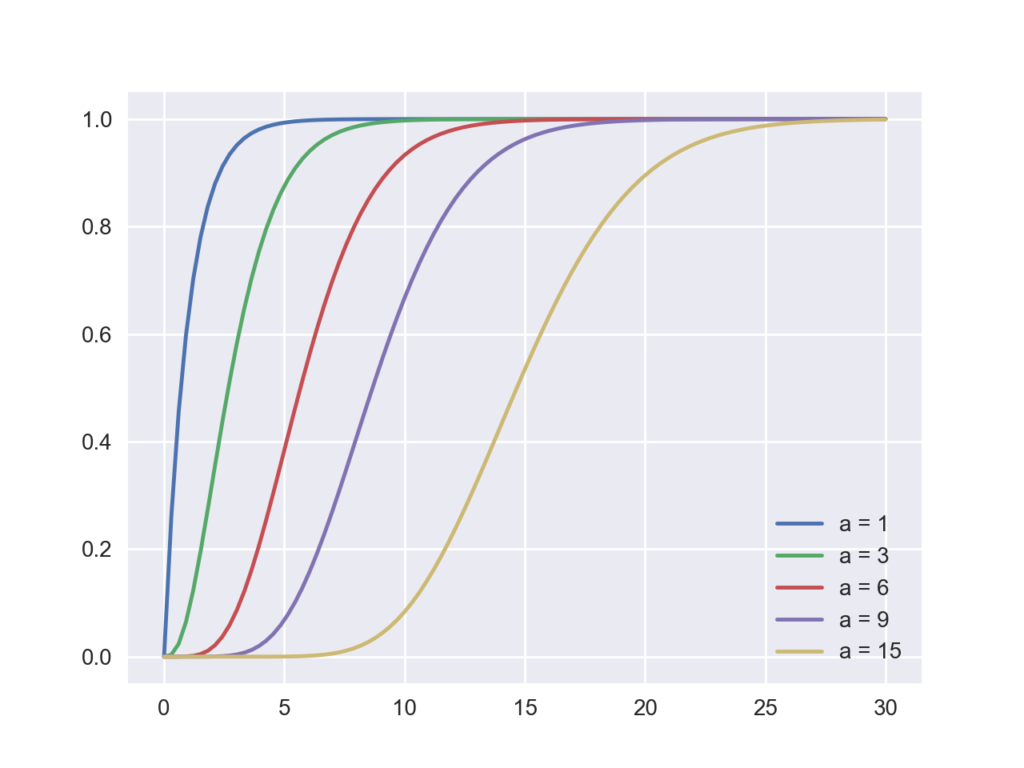
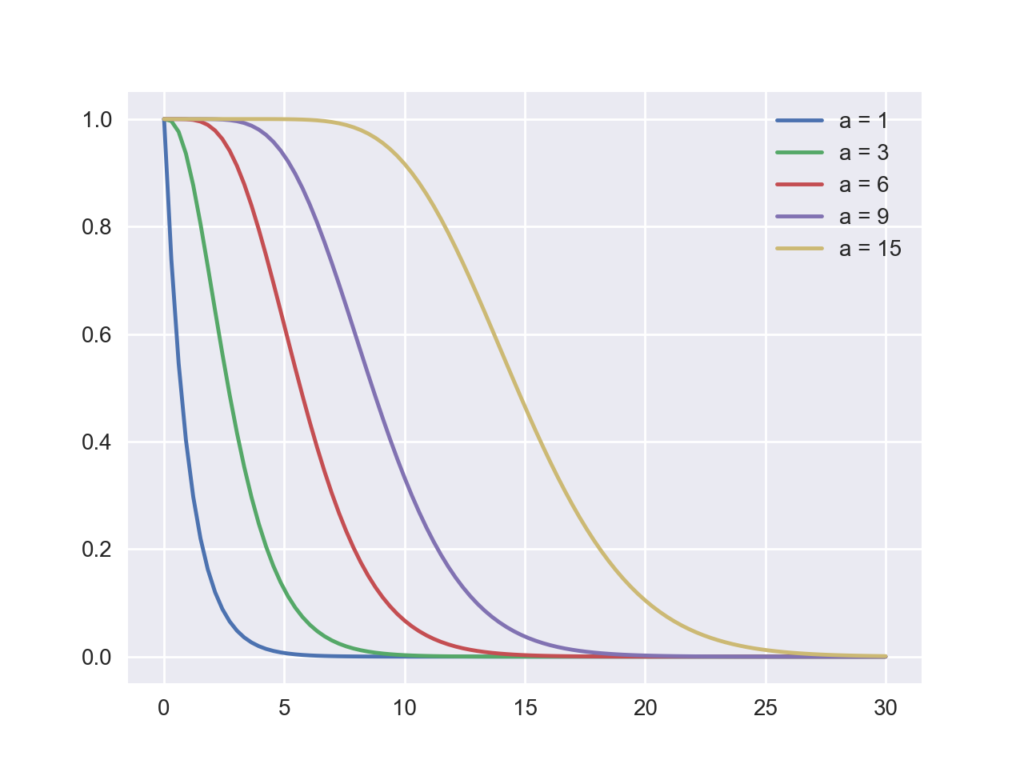
名前の通り確率密度関数を指定点まで積分した関数を返します.ある点以下の事象が起きる確率になります.以下のコードではaの値を変えたガンマ分布の累積分布関数を描いています.
x = np.linspace(0,30,100)
for i in [1,3,6,9,15]:
gamma_cdf = stats.gamma.cdf(x, i)
plt.plot(x, gamma_cdf, label='a = {}'.format(i))
plt.legend(loc='best')
生存関数
累積分布関数とは逆に,ある点以上の事象が起こる確率を与えます.「1-cdf」と同じです.以下のコードでは上記の累積分布関数と同じようにaの値を変えながらガンマ関数の生存関数を描いています.これらを比べることで2つの関係性が理解しやすくなると思います.
for i in [1,3,6,9,15]:
gamma_sf = stats.gamma.sf(x, i)
plt.plot(x, gamma_sf, label='a = {}'.format(i))
plt.plot(loc='best')
%点関数
累積分布関数が指定した値を取る,変数を返します.cdfの逆関数です.例えばppf(0.50)は中央値ですし,ppf(0.10)は下側10%点になります.下記のコードのように,ある確率分布関数の描画範囲を決める時に,例えば1%点から99%点の間を求めることがよく行われます.
x = np.linspace(stats.norm.ppf(0.01, loc=50, scale=10),
stats.norm.ppf(0.99, loc=50, scale=10),
100)
plt.plot(x, stats.norm.pdf(x, loc=50, scale=10))
逆生存関数
生存関数の逆関数です.上位5%の値を知りたい場合isf(0.95),四分位点を知りたい場合isf(0.25)などに有用です.以下のコードでは平均50loc=50,標準偏差10scale=10の正規分布のトップ1,5,10%に入る値を表示しています.
targets = [0.01, 0.05, 0.1]
for t in targets:
print('top {}%: {:.2f}'.format(100*t, stats.norm.isf(t, loc=50, scale=10)))
top 1.0%: 73.26 top 5.0%: 66.45 top 10.0%: 62.82
インターバル
指定した確率を与える値の範囲を中央値を挟んで返します.例えば95%の値が含まれる範囲などを求める際に使えます.以下の例では平均50loc=50,標準偏差20scale=20の正規分布の95%alpha=0.95が入る範囲を表示しています.
bottom, up = stats.norm.interval(alpha=0.95, loc=50, scale=20)
print('{:.2f} < x < {:.2f}'.format(bottom, up))
10.80 < x < 89.20
固定型統計分布: frozen RV
上記までの例では指定した確率分布の形はメソッドを呼び出す度に指定していました.しかし,先に望みの形の確率分布変数を作って,そのあとにメソッドを呼び出すこともできます.このような変数をフローズン(frozen)確率変数と呼びます.
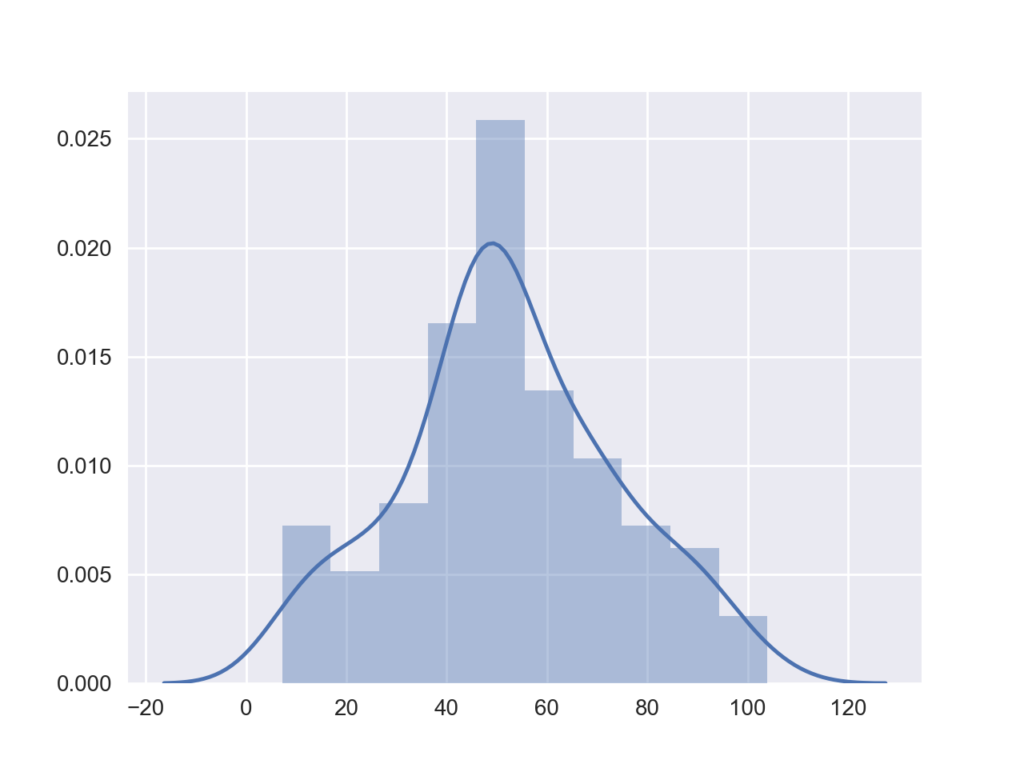
以下の例ではまず平均50loc=50,標準偏差20scale=20の正規分布を作成し,そのあとでサンプル数100size=100を得ています.確率分布に対する操作が1つだけの場合にはあまり恩恵が感じられませんが,色々とあとで使い回したい場合にはこちらの方がコードの量が減って便利だと思います.
frozen_normal = stats.norm(loc=50, scale=20) rvs = frozen_normal.rvs(size=100) sns.distplot(rvs, bins=10)
終わりに
上で見たようにscipy.statsには様々な確率分布が実装されていて,ほぼ同様の操作で扱うことができます.きちんと確率・統計学の学習を進めて確率分布の性質に習熟すればすぐにコードに落とし込むことが可能です.統計の学習を進めていけばすぐにコードに反映できるというのは安心ですね.しっかりと学習を進めていきましょう.
コメント