計算化学では分子軌道を,構成原子の原子軌道の線形結合で表現します.これまでさまざまな原子軌道を表す関数が提唱されています.このような原子軌道を表す関数を基底関数(basis function)と呼び,その集まりを基底関数系(basis set)といいます.
基底関数系は量子化学計算の精度を決める大切な構成要素であり,精度の改善を目指して多くの人によって色々な形のものが報告されています.このような今まで報告されている基底関系を一カ所に集めたデータベースが「Basis Set Exchange(BSE)」になります.
2007年の公開以来,ソフトを用いて計算化学を利用する多くのエンドユーザーに支持されるばかりでなく,理論開発研究者の間でも論文の著者自身が新たなデータを配布するプラットフォームとして用いられています.基底関数系の入手先を一元化することで,異なるユーザー・ソフトウェア間においても計算の再現性を担保しやすくなりました.
この記事では2019年になって一新された新生BSEについて,WEBインターフェースやPython APIの使い方について触れ,実際にBSEから取得した基底関数系をPsi4を用いた量子化学計算に適用してみます.
“New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community” J. Chem. Inf. Model. 2019, 59, 4814-4820.

Basis Set Exchangeとは
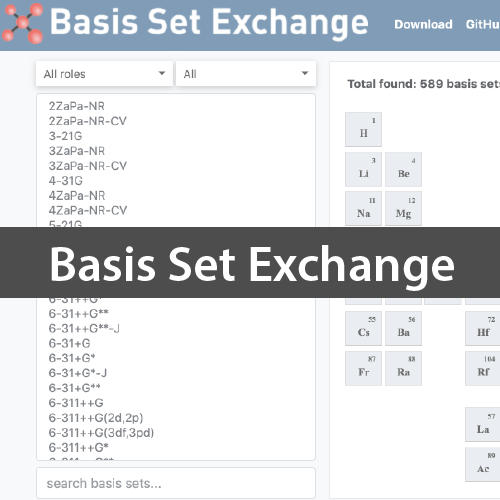
Basis Set Exchangeは基底関数に関する包括的なデータベースです.下のようにWEBサイト上で,
- 左側:基底関数系の一覧から選択
- 右側:周期表から興味のある元素を選択
どちらかを選択することで,総数600近くから絞り込んでいきます.
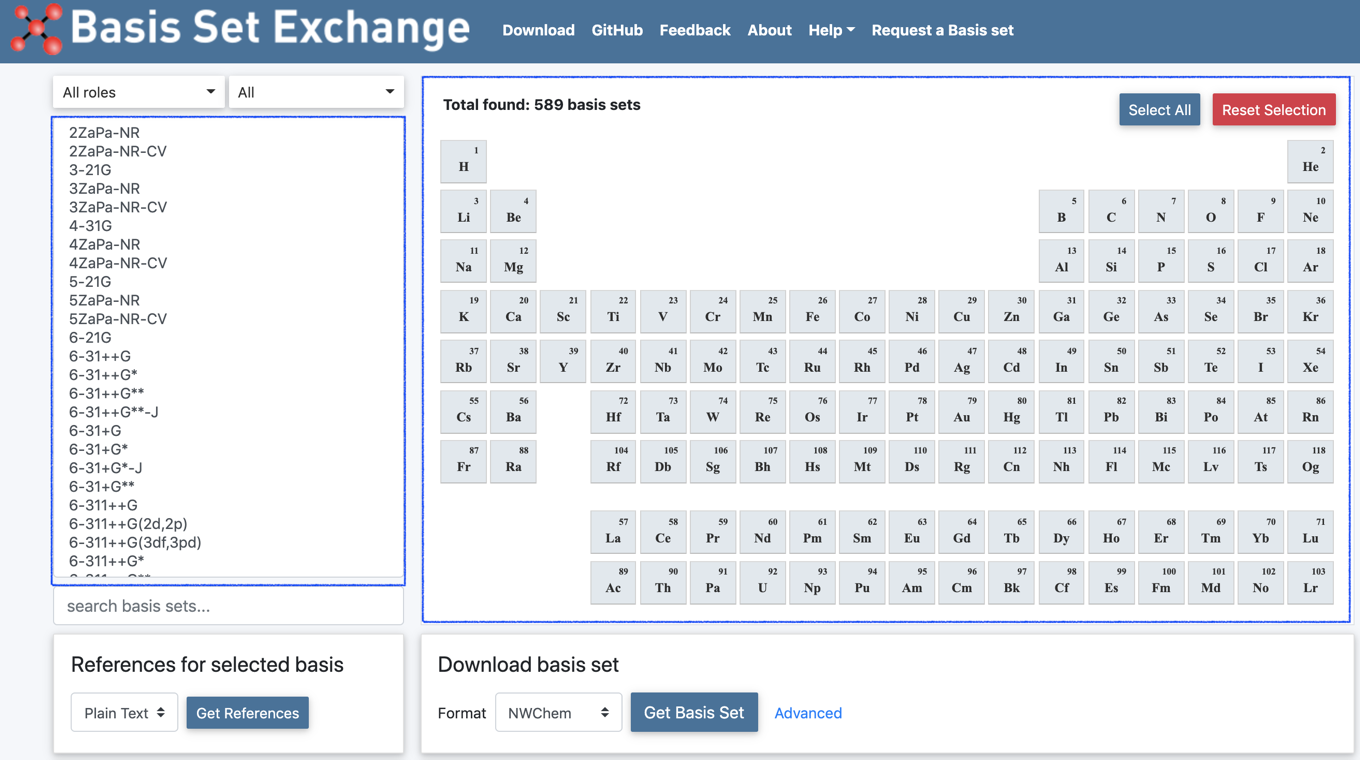
また選択した基底関数系は,各種計算化学用ソフトウェアに対応した形式にてダウンロードが可能になっています.

ここではヨウ素を含む化合物のハロゲン結合の計算でたびたび用いられるLanL2DZ(d,p)をダウンロードしてみます.こちらはGaussian16やpsi4にはデフォルトでは組み込まれていませんので,BSEから入手する必要があります.
今回は「psi4」形式で試してみます.
- LANL2DZdp
- ヨウ素
- psi4
が選択されていることを確認します.
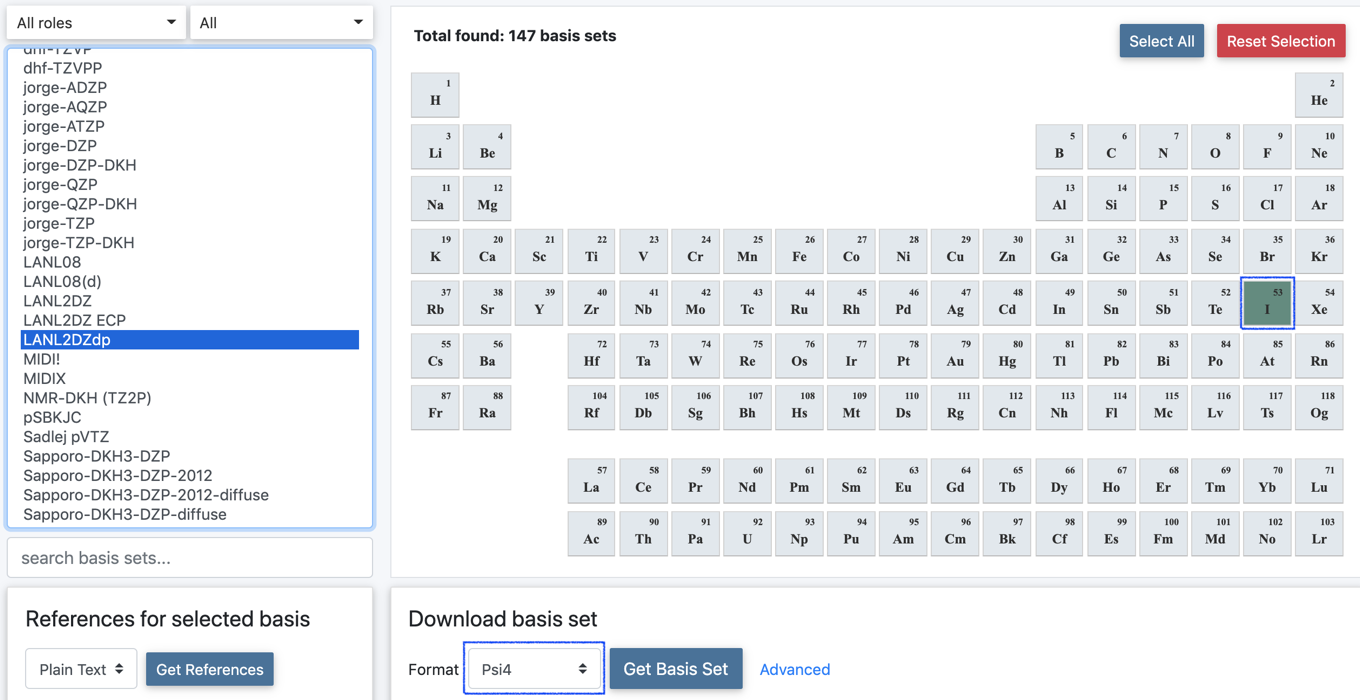
「Get Basis Set」をクリックすることでテキストファル形式のウィンドウが現れます.「Download」ボタンを押すことで望みの基底関数系が入手できました.
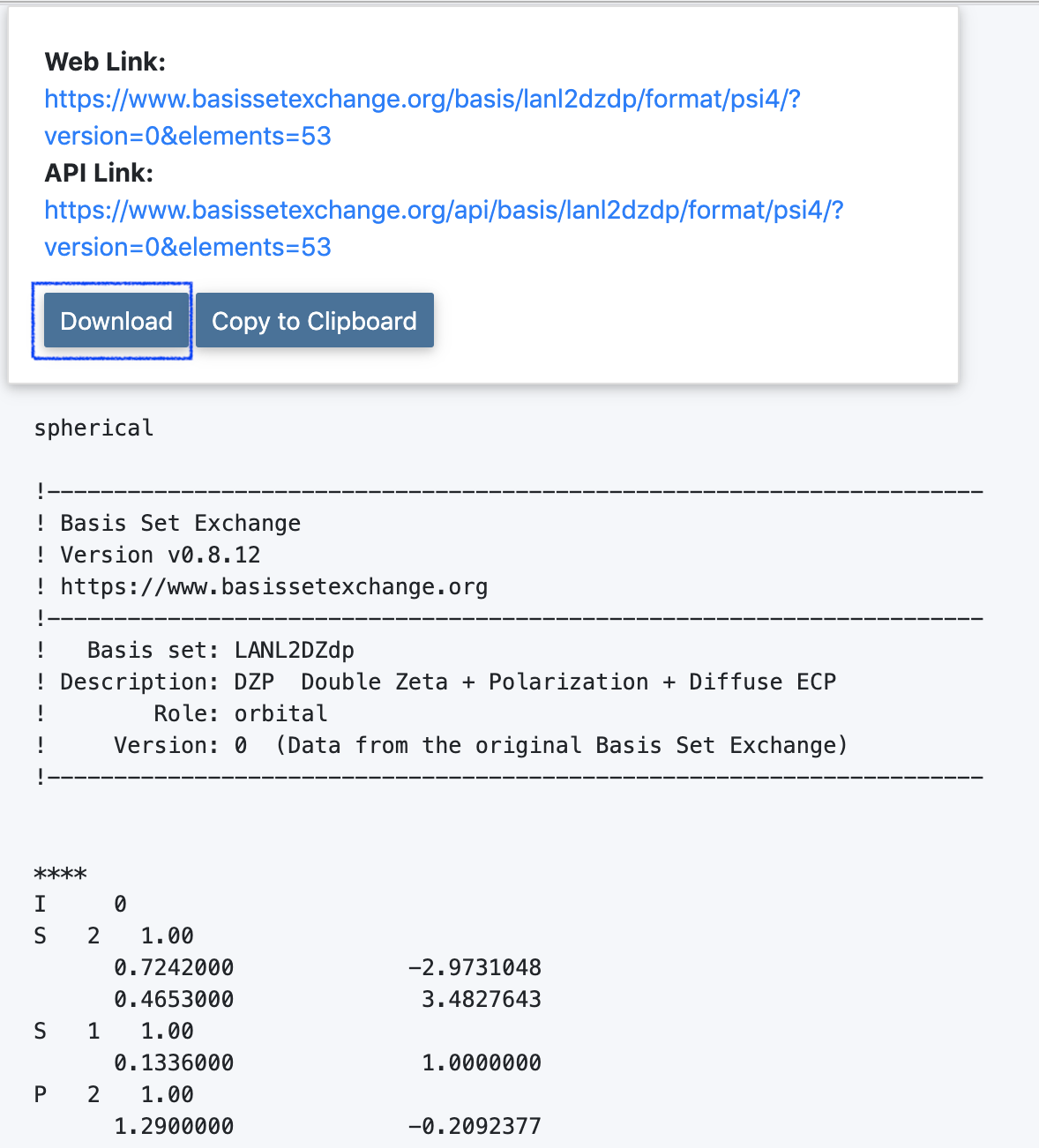
Basis Set Exchangeをpythonから使う
新しくなったBSEではpythonから操作可能なライブラリが用意されており,pipでインストール可能です.
pip install basis_set_exchange
コマンドラインから,またはpythonスクリプト中で機械的に任意の基底関数系を取得可能です.
この記事ではpythonスクリプト中での使い方をみてみます.
pythonライブラリの利用法
pythonライブラリの「basis_set_exchange」でもget_basis関数を用いて,
- どの基底関数系を
- どの原子に対して(原子番号で指定)
- どのフォーマットで
ダウンロードするかを指定します.
先ほどと同じく,ヨウ素用のLanL2DZ(d,p)をpsi4用フォーマットで入手します.
import basis_set_exchange as bse
lanl2dzdp = bse.get_basis('lanl2dzdp', elements=[53], fmt='psi4')
print(lanl2dzdp)
得られたデータはpythonの文字列オブジェクトになります.このオブジェクトを後ほど,psi4を用いた独自の基底関数系設定のところで利用していきます.
spherical !---------------------------------------------------------------------- ! Basis Set Exchange ! Version v0.8.12 ! https://www.basissetexchange.org !---------------------------------------------------------------------- ! Basis set: LANL2DZdp ! Description: DZP Double Zeta + Polarization + Diffuse ECP ! Role: orbital ! Version: 0 (Data from the original Basis Set Exchange) !---------------------------------------------------------------------- ...略 **** I 0 I-ECP 3 46 f potential 5 0 1.0715702 -0.0747621 1 44.1936028 -30.0811224 2 12.9367609 -75.3722721 2 3.1956412 -22.0563758 2 0.8589806 -1.6979585 s-f potential 5 0 127.9202670 2.9380036 1 78.6211465 41.2471267 2 36.5146237 287.8680095 2 9.9065681 114.3758506 2 1.9420086 37.6547714 p-f potential 5 0 13.0035304 2.2222630 1 76.0331404 39.4090831 ...略
Psi4で基底関数系の設定方法
「計算化学における電荷:psi4を用いた電子密度解析」などの記事ではPsi4を用いた計算では例えば,
psi4.energy('mp2/sto-3g', molecule=mol)
のようにエネルギー計算を実行する関数の中で基底関数系を指定していました.計算で用いる基底関数系はbasisという(グローバル)オプション変数で指定できますので,上記コードは以下のものと同じです.
psi4.set_options({'basis': 'sto-3g'})
psi4.energy('mp2', molecule=mol)
それでは原子の種類ごとに異なる基底関数系を用いて計算を行いたい場合はどうすればよいでしょうか?
basisとして独自に定義した基底関数系を用いればよいです.
基底関数系を独自に定義
原子毎に異なる基底関数系を用いて計算する際には,「どの原子にどの基底関数系を用いるか」を以下のようなフォーマットで記していきます.
PsiAPI以前から使われている記法をそのまま移植しているためpythonicではないフォーマットですが,この形式のブロックを連ねてstringオブジェクトとして作成します.
このようにして得た文字列をbasis_helper関数に渡すことで,作成した独自の定義をbasisオプションとして設定できるようになります.
この説明ではややわかりにくいと思いますので,以下でメタンを用いてコード例を示します.
ここではmybs1とmybs2という2つを定義しています.
- mybs1:全ての原子にSTO-3Gを設定(通常のSTO-3Gと実質同じ)
- mybs2:炭素に3-21Gを,残りの原子にSTO-3Gを設定
bs2では最初全ての原子にSTO-3Gを割り当てていますが,そのあとで炭素を3-21Gに上書きしています.
basis_helperではset_optionをFalseにしない場合は,basisオプションに作成した定義をそのまま設定しますので,すぐに利用可能です.
以下のコードでは確認と学習のためにpsi4.core.BasisSet.buildを用いて,ログファイルに独自の定義の詳細を描き込んでいます.
import psi4
psi4.set_output_file('CH4_bs.txt')
mol1 = '''
0 1
C 0.12632979 -0.69148935 0.00000000
H 0.48298421 -1.70029935 0.00000000
H 0.48300263 -0.18709116 0.87365150
H 0.48300263 -0.18709116 -0.87365150
H -0.94367021 -0.69147617 0.00000000
'''
mybs1 = '''
assign sto-3g
'''
mybs2 = '''
assign sto-3g
assign C 3-21G
'''
psi4mol = psi4.geometry(mol1)
psi4.basis_helper(mybs1, name='mybs1')
f1 = psi4.core.BasisSet.build(psi4mol)
f1.print_detail_out()
psi4.basis_helper(mybs2, name='mybs2')
f2 = psi4.core.BasisSet.build(psi4mol)
f2.print_detail_out()
ログファイルの内容を一部抜粋してみます.
Name: MYBS1
Role: ORBITAL
Keyword: None
atoms 1 entry C line 61 file /Users/.../psi4/basis/sto-3g.gbs
atoms 2-5 entry H line 19 file /Users/.../psi4/basis/sto-3g.gbs
...
Name: MYBS2
Role: ORBITAL
Keyword: None
atoms 1 entry C line 68 file /Users/.../psi4/basis/3-21g.gbs
atoms 2-5 entry H line 19 file /Users/.../psi4/basis/sto-3g.gbs
さらに分子の入力座標を工夫することで,同じ元素の異なる原子毎に異なる基底関数系を指定することも可能です.
以下の例ではメタンの水素を3種類(H, H2, H3)にわけ,それぞれに
- H:sto-3g
- H2:cc-pVDZ
- H3:pp-pVTZ
のように異なる基底関数系を割り当てたmybs3を定義しています.
mol2 = ''' 0 1 C 0.12632979 -0.69148935 0.00000000 H 0.48298421 -1.70029935 0.00000000 H2 0.48300263 -0.18709116 0.87365150 H2 0.48300263 -0.18709116 -0.87365150 H3 -0.94367021 -0.69147617 0.00000000 ''' mybs3 = ''' assign sto-3g assign H2 cc-pVDZ assign H3 cc-pVTZ ''' psi4mol2 = psi4.geometry(mol2) psi4.basis_helper(mybs3, name='mybs3') f3 = psi4.core.BasisSet.build(psi4mol2) f3.print_detail_out()
同様にログファイルを抜粋します.
Name: MYBS3
Role: ORBITAL
Keyword: None
atoms 1 entry C line 61 file /Users/.../psi4/basis/sto-3g.gbs
atoms 2 entry H line 19 file /Users/.../psi4/basis/sto-3g.gbs
atoms 3-4 entry H line 22 file /Users/.../psi4/basis/cc-pvdz.gbs
atoms 5 entry H line 23 file /Users/.../psi4/basis/cc-pvtz.gbs
もっともこの例のように分子内の異なる水素にそれぞれ違った基底関数をわりあてて計算することはまずありません.こういった指定法が最も使われるのが,次節で説明する「ECP(有効内殻ポテンシャル)」の指定です.
psi4を用いたECPの設定
ここではヨウ化メチルと塩化物イオンからなる系の計算を考えてみます.その際,
- 水素・炭素・塩素
- ヨウ素
の2種類について別々の基底関数系を割り当てていき,ヨウ素についてはECPを用いることとします.ECPとしては元々psi4で利用可能な「LanL2DZ」に加えて,先ほどBSEから取得した「LanL2DZ(d,p)」を用いることで以下のように5つの形式を定義します.
| 名前 | 水素・炭素・塩素 | ヨウ素 |
|---|---|---|
| bs1 | aug-cc-pVDZ | LanL2DZ |
| bs2 | aug-cc-pVTZ | LanL2DZ |
| bs3 | aug-cc-pVDZ | LanL2DZ(d,p) |
| bs4 | aug-cc-pVTZ | LanL2DZ(d,p) |
| bs5 | aug-cc-pVQZ | LanL2DZ(d,p) |
BSEからダウンロードしたデータを用いて,指定の原子に割り当てるには以下のように[original-bs]を定義して,それをassignしていきます.「中身」と書いてある部分にダウンロードした文字列オブジェクトを用います.
[original-bs]
中身・・・
具体例を見た方がわかりやすいと思います.
以下では[ecp]という名前で定義しています.basis_helper関数のset_optionをFalseにしていますので,この段階ではbasisオプションには何も設定されていません.
import psi4
import basis_set_exchange as bse
lanl2dzdp = bse.get_basis('lanl2dzdp', elements=[53], fmt='psi4')
bs1 = '''
assign aug-cc-pVDZ
assign I lanl2dz
'''
bs2 = '''
assign aug-cc-pVTZ
assign I lanl2dz
'''
bs3 = '''
assign aug-cc-pVDZ
assign I ecp
[ecp]
{}'''.format(lanl2dzdp)
bs4 = '''
assign aug-cc-pVTZ
assign I ecp
[ecp]
{}
'''.format(lanl2dzdp)
bs5 = '''
assign aug-cc-pVQZ
assign I ecp
[ecp]
{}
'''.format(lanl2dzdp)
psi4.basis_helper(bs1, name='bs1', set_option=False)
psi4.basis_helper(bs2, name='bs2', set_option=False)
psi4.basis_helper(bs3, name='bs3', set_option=False)
psi4.basis_helper(bs4, name='bs4', set_option=False)
psi4.basis_helper(bs5, name='bs5', set_option=False)
Psi4でECPを用いてハロゲン結合のエネルギーを計算
続いてヨウ化メチルと塩化物イオンを用いて,前項で定義した5つの手法を用いてヨウ素ー塩素距離を変えながら相互作用エネルギーを求めていきます.その際,ハロゲン結合の角度特異性を考えて塩化物イオンは炭素ーヨウ素結合の延長線上に位置することとします
まずはライブラリのインポートと,塩化物イオンの位置を決めるためのC-I結合に平行な単位ベクトルを求めます.
import psi4
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
import time
au2kcal = psi4.constants.hartree2kcalmol
now = time.strftime('%Y%m%d-%H%M')
psi4.set_num_threads(10)
psi4.set_memory('14GB')
psi4.set_output_file(now + '_BSE.log')
geom = '''
0 1
C -2.32047871 -0.58510637 0.00000000
H -1.96382429 -1.59391638 0.00000000
H -1.96380587 -0.08070818 0.87365150
H -3.39047871 -0.58509319 0.00000000
I -1.62046660 0.40483400 -1.71464314
--
-1 1
Cl {} {} {}
'''
r0 = np.array([-2.32047871, -0.58510637, 0.00000000])
r1 = np.array([-1.62046660, 0.40483400, -1.71464314])
r = (r1 - r0)/np.sqrt(np.sum((r1 - r0) ** 2))
以下のコードで実際にエネルギーを計算しています.なおDFTの汎関数にはwB97X-Dを用いています.
calc_energy関数では,錯体のエネルギーに加えて,「Psi4で分子間相互作用エネルギーの計算:超分子法と基底関数重なり誤差」で解説したCP法を用いた相互作用エネルギーを計算します.set_options({‘basis’: bs})の部分で用いる基底関数系をbasisオプションに設定しています.
この関数を用いて原子間距離を1.5から4.4Åまで0.1Åずつ変えながら,先ほど定義したbs1からbs5を用いてエネルギー計算を行います.
basis_set = ['bs1', 'bs2', 'bs3', 'bs4', 'bs5']
def calc_energy(molecule, bs):
psi4.set_options({'basis': bs})
int_E = psi4.energy('wb97x-d', bsse_type='cp', molecule=molecule)
calc_E = psi4.energy('wb97x-d', molecule=molecule)
psi4.core.clean()
return int_E * au2kcal, calc_E
electronic_energy = []
int_energy = []
for i in np.arange(1.5, 4.5, 0.1):
x, y, z = r * i + r1
psi4mol = psi4.geometry(geom.format(x, y, z))
calced_e = []
calced_i = []
for bs in basis_set:
int_e, calc_e = calc_energy(psi4mol, bs)
calced_i.append(int_e)
calced_e.append(calc_e)
electronic_energy.append(calced_e)
int_energy.append(calced_i)
df1 = pd.DataFrame(electronic_energy, index=[0.1*i for i in range(15,45)])
df2 = pd.DataFrame(int_energy, index=[0.1*i for i in range(15,45)])
df1.columns = ['bs1', 'bs2', 'bs3', 'bs4', 'bs5']
df2.columns = df1.columns
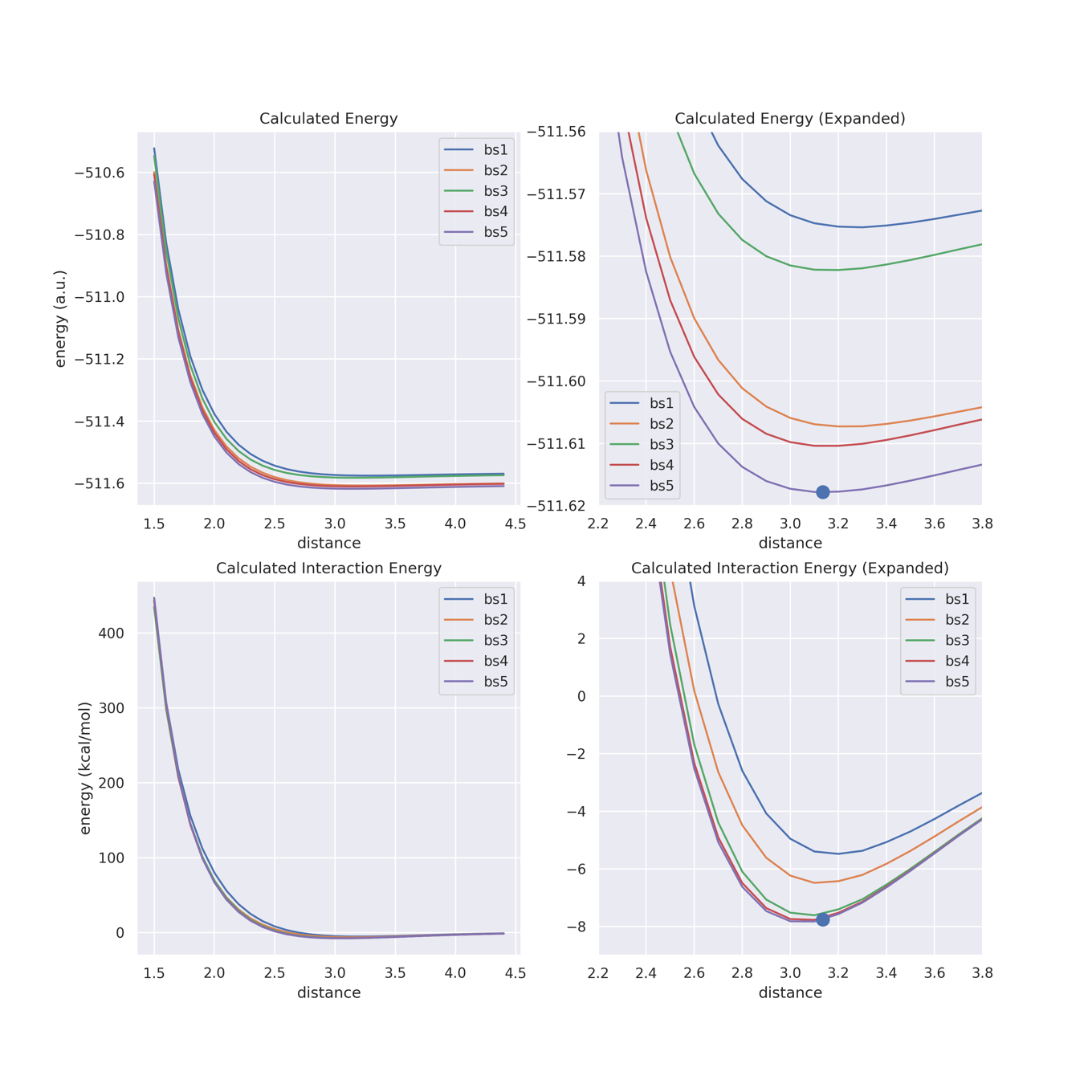
得られた結果の全体図と拡大図が以下のようになります.bs5を用いて最小エネルギーを与える点も併せて示しておきました.この距離(約3.13Å)での相互作用エネルギーは約-7.7 kcal/molでした.
ヨウ素はサイズの大きい原子ですので,近距離(2.5Å以下)では反発が非常に大きいことが見てとれます.また相互作用エネルギーの大きさに関しては,塩化物イオンの基底関数系を大きくする(bs1 vs bs2)よりもヨウ素上のECPを変える(bs1 vs bs3)の方が影響が大きいこともわかります.
おわりに
今回は「Basis Set Exchangeは基底関数系に関するデータベース:PythonとPsi4を用いてECPを自在に扱う」という話題について,
- Basis Set Exchange(BSE)とはなにか
- BSEのWEBインターフェースの使い方
- BSEをpythonスクリプトからの利用方法
- Psi4で独自の基底関数系を定義する方法
- ヨウ化メチルと塩化物イオンを例としたエネルギー計算
などについてみてきました.今回の内容を消化することで,分子中の原子について思い通りの方法で基底関数系を割り当てて計算可能になったことと思います.
コメント