本ブログではオープンソースの量子化学計算ソフトPsi4を用いて,計算化学を基礎から説明しています。「計算化学の構造最適化の基本をPsi4で学ぶ」という記事で触れたように,Psi4では構造最適化エンジンとしてOptkingが採用されています。
Optkingのオプションを適切に設定することで,ほとんどの分子の構造最適化に対応可能です。それでも通常のアプローチでは最適化がスムーズに進行しない分子系も存在します。そのような場合に利用可能な手段として,Psi4ではGeomeTRICと呼ばれる外部最適化エンジンとの連携が可能となっています。
GeomeTRIC自体はPsi4のみならず,GaussianやMolproなど,様々な量子化学計算プログラムを計算エンジンとして利用できる独立したプログラムです。Psi4では,このGeomeTRICをPsi4のプログラム側から呼び出して利用可能です。
今回の記事ではPsi4を通したGeomeTRICの使い方について,
- GeomeTRICとは何か
- Psi4からGeomeTRICを使う方法
- Optkingにおける制約付き最適化の復習
- GeomeTRICを用いた制約付き最適化の方法
などについて触れていきます。独立したプログラムとしてのGeomTRIC(geometric-optimize)の使い方に関しては公式ドキュメントを参照してください。

GeomeTricとは
GeomeTRICはTRIC(Translation-Rotation-Internal Coordinate)と呼ばれる座標系を利用した構造最適化エンジンです。TRICは水分子のクラスターなど,複数分子からなる系の構造最適化を効率的に行うために開発された内部座標系です。並進および回転座標系を用いることで,分子内と分子間の相互作用を切り分けた記述が可能となり,さまざまな分子系の構造最適化が効率的に進行することが示されています。複数分子の最適化に限らず,既存の座標系を用いるとポテンシャルエネルギー曲面が平坦になりがちな難易度の高い構造最適化において力を発揮します。
“Geometry optimization made simple with translation and rotation coordinates.” J. Chem. Phys. 2016, 144, 214108.
前述のようにGeomeTRICは本来はコマンドラインから使うソフトウェアであり,以下のコマンドのようにconda
conda install geometric -c conda-forge
またはpipでインストール可能です。
pip install geometric
インストールが完了するとターミナルからgeometric-optimizeというコマンドが利用可能になるほか,Psi4中からGeomeTRICとの連携が可能になります。ただしPsi4からはGeomeTRICの全ての機能にアクセスできるわけではありません。
Psi4からGeomeTricを利用する
Psi4からGeomeTRICを利用するには,psi4.optimizeのengineオプションでgeometricを指定します。デフォルトはoptkingです。またoptimizer_keywordsにGeomeTRICで用いる設定をJSON形式で渡します。
Optkingではpsi4.set_optionsを用いて最適化の振舞いを設定しました。例えばGEOM_MAXITERで構造最適化のサイクル数を変更できます(デフォルトは50回)。この値はGeomeTRICを用いる際にも引き継がれます。
また構造最適化の収束条件を決めるG_CONVERGENCEのデフォルトはQCHEMですが,GeomeTRICではQCHEMの値が存在しないためGAU_TIGHTに自動的に変更されます。
以下のコードでは水分子を対象に,OptkingとGeomeTRICの2つの最適化エンジンを用いてHF/STO-3Gレベルで構造最適化計算を行います。最後に得られたエネルギーと最適化構造を出力しています。なお最初のOptkingを用いた最適化でデカルト座標系を用いているのは構造最適化の途中で対称性が変化してしまい計算が止まってしまうためです。この場合もGeomeTRICを用いた最適化ではTRICが使われています。
import psi4
water = psi4.geometry("""
0 1
O -0.30493706 1.20522747 0.00000000
H 0.65506294 1.20522747 0.00000000
H -0.62539165 2.11016331 0.00000000
""")
water2 = water.clone()
psi4.set_options({'opt_coordinates': 'cartesian'})
# Optkingで最適化
psi4.set_output_file('water_optking.log')
energy_optking = psi4.optimize('hf/sto-3g', molecule=water)
# GeomeTRICで最適化
psi4.set_output_file('water_geometric.log')
energy_geometric = psi4.optimize('hf/sto-3g',
molecule=water2,
engine='geometric')
print(f'energy from Optking: {energy_optking: .4f} au')
print(f'optimized structure\n{water.save_string_xyz()}')
print(f'energy from GeomeTRIC: {energy_geometric: .4f} au')
print(f'optimized structure\n{water2.save_string_xyz()}')
出力結果は以下のようになりました。同じ値のエネルギーが得られていますが,収束構造が異なっているのがわかります。
energy from Optking: -74.9660 au optimized structure 0 1 O -0.041067649486 -0.058110478598 0.000000000000 H 0.944972988130 0.023598842258 0.000000000000 H -0.293199588832 0.898656622689 0.000000000000 energy from GeomeTRIC: -74.9660 au optimized structure 0 1 O -0.067244419672 -0.095148648120 0.000000000000 H 0.918799318093 -0.013440884980 0.000000000000 H -0.319371453708 0.861611703298 0.000000000000
Psi4ではログファイル中の重要な行には「~」が出力されています。これを目印に構造最適化の途中経過をログファイルからgrepコマンドで取り出し,比べてみます。
grep '~' water*.log
以下がOptkingで最適化した結果です。11ステップで最適化が終了していることがわかります。
--------------------------------------------------------------------------------------------------------------- ~
Step Total Energy Delta E MAX Force RMS Force MAX Disp RMS Disp ~
--------------------------------------------------------------------------------------------------------------- ~
1 -74.96078853 -7.50e+01 5.96e-02 3.03e-02 o 3.27e-01 1.67e-01 o ~
2 -74.89618132 6.46e-02 1.85e-01 9.97e-02 o 7.49e-02 4.17e-02 o ~
3 -74.92991570 -3.37e-02 1.45e-01 7.90e-02 o 1.80e-01 9.14e-02 o ~
4 -74.96520734 -3.53e-02 2.26e-02 1.13e-02 o 6.69e-02 3.18e-02 o ~
5 -74.96591627 -7.09e-04 4.85e-03 2.62e-03 o 2.70e-02 1.34e-02 o ~
6 -74.96594315 -2.69e-05 3.68e-03 2.01e-03 o 1.29e-02 6.56e-03 o ~
7 -74.96598334 -4.02e-05 2.23e-03 1.31e-03 o 4.53e-03 2.12e-03 o ~
8 -74.96598896 -5.61e-06 8.69e-04 5.24e-04 o 1.73e-03 7.13e-04 o ~
9 -74.96598941 -4.58e-07 * 8.70e-04 4.84e-04 o 3.00e-03 1.47e-03 o ~
10 -74.96598652 2.89e-06 1.99e-03 1.07e-03 o 2.80e-03 1.23e-03 o ~
11 -74.96599012 -3.60e-06 9.40e-06 * 5.12e-06 o 1.20e-05 * 5.30e-06 o ~
続いてGeomeTRICで最適化した結果です。この場合は6ステップで最適化が終了しています。前述の通り「Convergence Criteria」が変更されていることも確認できます。
--------------------------------------------------------------------------------------------- ~
Step Total Energy Delta E MAX Force RMS Force MAX Disp RMS Disp ~
--------------------------------------------------------------------------------------------- ~
Convergence Criteria 1.00e-06 1.50e-05 1.00e-05 6.00e-05 4.00e-05 ~
--------------------------------------------------------------------------------------------- ~
0 -7.49607885e+01 -------- 7.30e-02 5.26e-02 -------- -------- ~
1 -7.49646576e+01 -3.87e-03 1.78e-02 1.65e-02 7.77e-02 7.17e-02 ~
2 -7.49659226e+01 -1.26e-03 5.66e-03 4.94e-03 3.96e-02 3.54e-02 ~
3 -7.49659890e+01 -6.65e-05 1.16e-03 9.02e-04 7.28e-03 5.97e-03 ~
4 -7.49659901e+01 -1.07e-06 8.21e-05 5.90e-05 6.64e-04 4.72e-04 ~
5 -7.49659901e+01 -5.97e-09 * 5.18e-07 * 4.23e-07 * 5.70e-05 * 4.52e-05 ~
6 -7.49659901e+01 -1.73e-11 * 1.20e-08 * 1.03e-08 * 8.62e-07 * 7.36e-07 * ~
ここまででPsi4を用いたGeomeTRICの利用法の基本を説明しました。GeomeTRICの強みは特に構造のスキャンなど制約付き最適化を実行する際に発揮されます。そこでまずはOptkingを用いた制約付き最適化について簡単に復習した後で,GeomeTRICを用いた方法を見ていきます。
Psi4のOptkingを用いた制約付き最適化
psi4.set_options({‘ranged_xxxx’: str}
Optkingで制約付き最適化を行いたい場合は,座標,結合,角度,二面角などのターゲットに対して
- frozen_xxxx
- ranged_xxxx
の2種類で制約を指定していきます。xxxxには
- cartesian(座標)
- distance(結合)
- bend(角度)
- dihedral(二面角)
のいずれかを用います。なお制約を施す原子の番号は1始まりで指定します。例えば以下のように使います。
psi4.set_options({'frozen_distance': '1 9',
'ranged_dihedral': '2 3 4 5 25 35'
})
この場合は1番目と9番目の原子間距離を固定し,原子2-3-4-5からなる二面角を25度から35度の間に制限します。
frozenは与えられた座標をそのまま固定するのに対し,rangedは条件を満たすような構造をPsi4が生成します。しかしこのPsi4による初期構造の生成には課題が多く,構造最適化が失敗することが多いです。
Problems with geometry convergence in dihedral scan – Geometry Optimization
「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事では,アルゴン二量体のエネルギーを計算する際に,以下のように1つのアルゴンのZ座標を変数として定義することで原子間距離のスキャンを行いました。これはranged_distanceを用いるとエラーが出やすいためです。
ar_geom = '''
0 1
Ar 0 0 0
Ar 0 0 {}
'''
アルゴン二量体のような単純な分子系では座標に変数を導入することは容易です。しかし構造が複雑になるにつれ,構造スキャンが可能なように分子を構築することが難しくなってきます。ところが「Psi4で遷移状態最適化:計算化学における虚振動と化学構造」という記事でも見たように,遷移状態の初期構造作成には構造スキャンがほぼ必須です。Psi4におけるこの課題を解決する方法としてGeomeTRICの利用があります。
GeomeTRICを用いた制約付き最適化の方法
GeomeTRICで構造の制約を指定する場合は,
- どの種類の制約を
- どのタイプの構造・座標に対して
- どの原子を対象に
設定するかを記述します。結合距離や角度などを設定する場合には「どの値に設定する」かの指定も必要です。
以下で指定方法を簡単に記した後で,具体例を通してGeomeTRICを用いた制約付き最適化の方法について見ていきます。
制約の種類
制約の種類としては
- freeze:初期構造のまま固定する
- set:指定した値に設定する
の2つが利用可能です。公式ドキュメントにはscanも記載されていますが,現在のところPsi4からはアクセスできないようです。
制約を課す対象
freezeまたはsetを行う対象には
- distance(結合)
- angle(角度;Psi4のbendとは異なるので注意)
- dihedral(二面角)
- xyz(座標)
などが挙げられます。
対象原子の指定
indicesに対して原子番号のリストで指定します。なお原子番号は0始まりで,これもPsi4とは異なる点に注意が必要です。
値の指定
setを用いる場合にはvalueを用いて値を設定します。
具体例1:結合距離の設定法
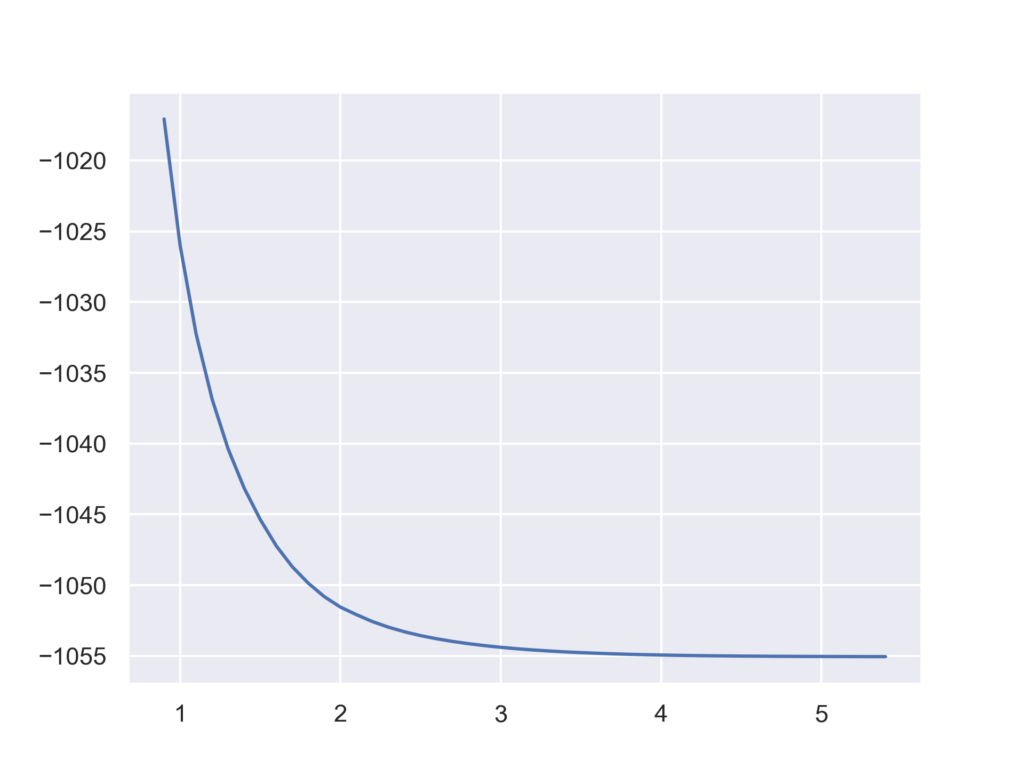
アルゴン二量体を例に原子間の距離をsetで指定してみます。以下のコードでは初期構造の0.9 Åから5.5 Åまで0.1Åずつ増加させながらループを回していきます。この例の場合は原子間距離だけが変数のため,構造最適化は不要ですがオプションの使い方を確認してください。
なおcoordsysオプションはデフォルトでTRICが選択されているため,なくても問題ありません。
import matplotlib.pyplot as plt
import numpy as np
import psi4
psi4.set_output_file('ar2.log')
ar2 = psi4.geometry("""
0 1
Ar 0 0 0
Ar 0 0 0.9
""")
distances = np.arange(0.9, 5.5, 0.1)
energies = []
for distance in distances:
print(f'distance: {distance: .2f} A')
geometric_keywords = {'coordsys': 'tric',
'constraints': {
'set': [{'type': 'distance',
'indices': [0, 1],
'value': distance}]
}
}
energy = psi4.optimize('wb97x-d/cc-pvdz',
molecule=ar2,
engine='geometric',
optimizer_keywords=geometric_keywords)
energies.append(energy)
plt.plot(distances, energies)
特にエラーが出ることなく,以下のようなグラフが得られました。
具体例2:二面角の設定法
続いてジフルオロエタンを例に二面角を変化・固定しながら構造最適化を行います。同様の作業を行う際に,「計算手法とエネルギー・最適化構造の関係:コンフォメーション探索における注意点」という記事ではケモインフォマティクス用ライブラリーのRDKitに二面角を設定した構造を生成させていました。これはPsi4でranged_dihedralを用いて構造を生成するとエラーが出てしまったからです。
今回の例ではGeomeTRICを用いて,Psi4内で完結するように二面角のスキャンを行ってみます。
import matplotlib.pyplot as plt
import psi4
psi4.set_output_file('dihedral.log')
mol = psi4.geometry("""
0 1
C -0.90513065 -0.61471441 0.00000000
H -0.54847622 -1.62352442 0.00000000
H -1.97513065 -0.61470123 0.00000000
C -0.39178843 0.11124186 1.25740497
H 0.67820976 0.10953479 1.25838332
H -0.74684499 1.12061487 1.25642758
F -0.45512286 0.02167583 -1.10227059
F -0.84381002 -0.52372244 2.35967391
""")
angles = range(180, -181, -15)
energies= []
for angle in angles:
geometric_keywords = {
'coordsys': 'tric',
'constraints': {
'set': [{'type': 'dihedral',
'indices': [6, 0, 3, 7],
'value': angle}]
}
}
print(f'angle: {angle: .1f}...')
energy = psi4.optimize('hf/sto-3g',
molecule=mol,
engine='geometric',
optimizer_keywords=geometric_keywords)
energies.append(energy)
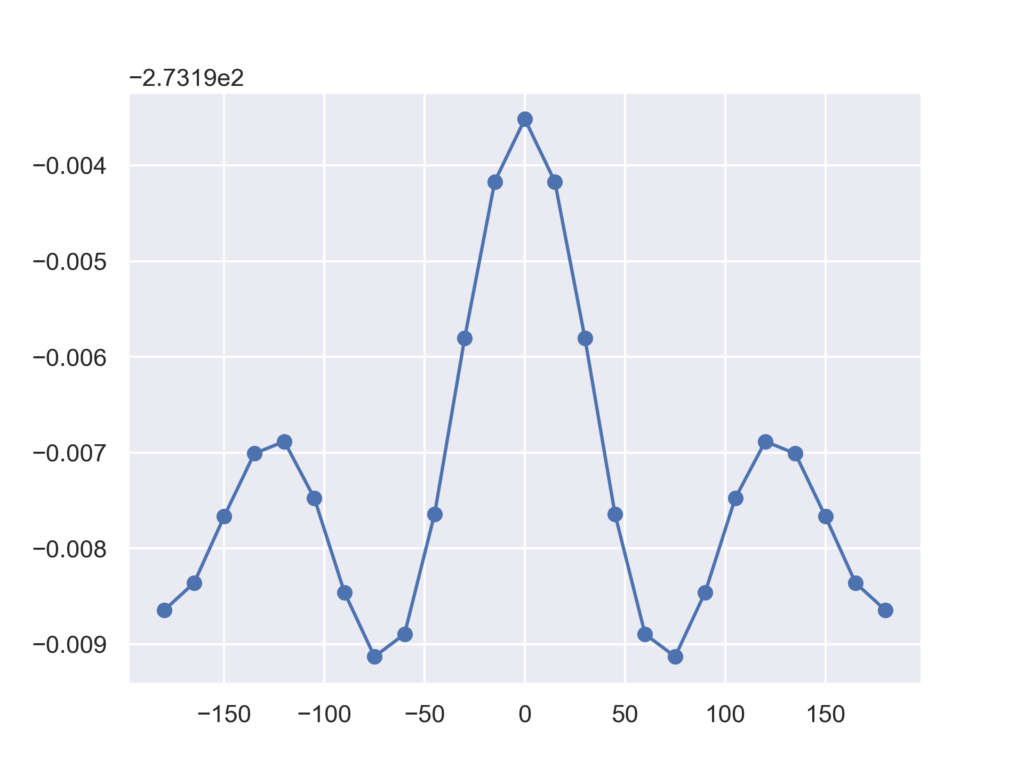
plt.plot(angles, energies, 'o-')
得られた結果は以下のグラフになりました。エラーが出ることなく,全ての構造で無事に最適化が終了しました。
終わりに
今回は「Psi4からGeomeTRICを使った構造最適化」という話題について、
- GeomeTRICとは何か
- Psi4からGeomeTRICを使う方法
- Psi4を用いた制約付き最適化の方法
- GeomeTRICを用いた制約付き最適化の方法
などについて,具体例を用いて説明してきました。
構造最適化は興味のある分子の性質を調べる上で最初に行う計算です。しかし量子化学計算の第一歩であるにも関わらず,エラーに悩まされることも少なくありません。そのような困難な最適化に遭遇した際に,GeomeTRICは有用なツールとなると思います。


コメント