「Psi4で溶媒効果を考慮する:PCM Solverの使い方」という記事では,
- 計算化学で溶媒効果を考慮する方法の一つとして連続誘電体モデル
- Psi4を用いてPCM Solverを使い,溶媒効果を考慮する方法
などについて紹介し,溶媒効果を考慮してどのように計算していくかを説明しました.例えば1,2−ジフルオロエタンを題材として双極子モーメントの大きいgauche体の方が極性溶媒中での安定化効果が大きくなることなどを確認しました.
連続誘電体モデルではこういった溶媒と溶質の長距離相互作用に関するモデル化法としてはとても有用です.一方で我々が興味のある系では,溶媒と溶質が水素結合などを通じて直接相互作用し溶質の構造を大きく変化させる場合もあります.今回はこのような場合のモデル化法として,溶媒分子をあらわに扱う方法について触れたいと思います.

PCMでは考慮できない溶媒効果
連続誘電体モデルは溶媒と溶質の静電相互作用など,長距離相互作用のモデル化には有効です.またパラメータ化を通じて,極性官能基の溶媒和によって得られる安定化エネルギーも考慮されています.
一方で連続誘電体モデルで考慮できない溶媒効果は水素結合などの近距離相互作用です.水素結合による極性官能基の安定化エネルギー自体は考慮されていますが,水素結合形成による基質構造の変化,ポテンシャルエネルギー曲面の形が大きくかわることは考慮できていません.
以前「psi4で遷移状態最適化:計算化学における虚振動と化学構造」という記事で,2-ピリドンから2-ヒドロキシピリジンへの互変異性を題材に遷移状態の最適化を扱いました.得られた遷移状態は水素原子が酸素から窒素原子へと移動する以下のような構造を示していました.
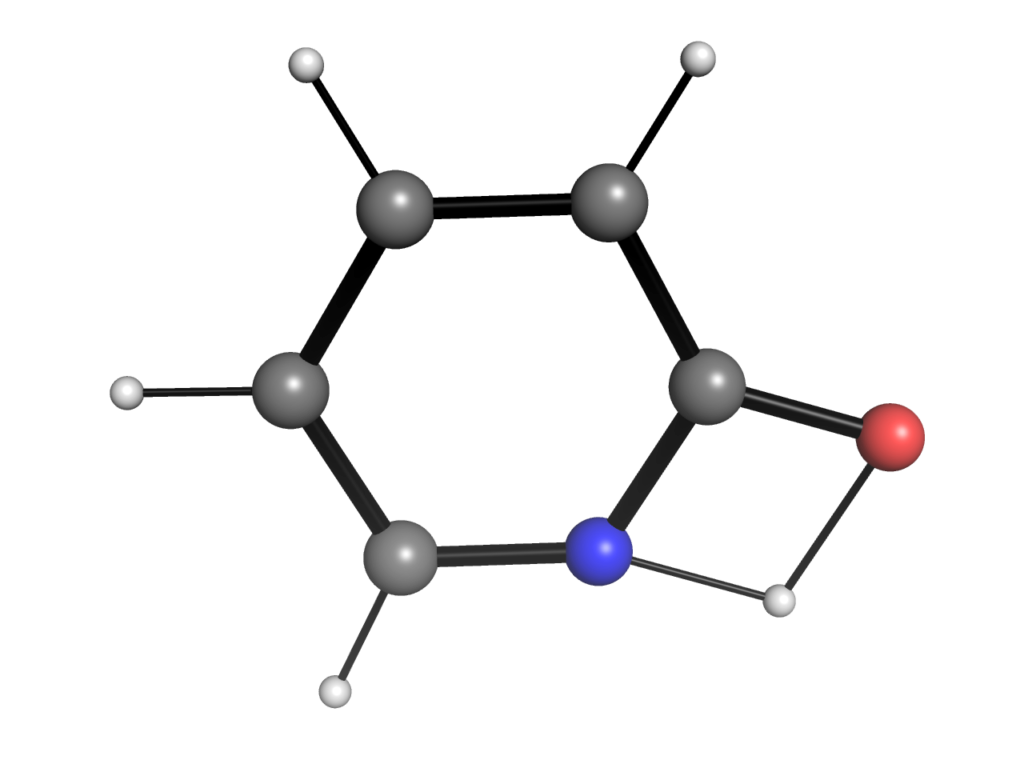
有機合成を学んだ方はこの4員環遷移状態はあまり好ましいように見えないかもしれません.例えば,水分子(またはアルコール分子)を1つ追加することで以下のような6員環遷移状態が実現できればより活性化エネルギーの低い反応経路が実現できそうです.
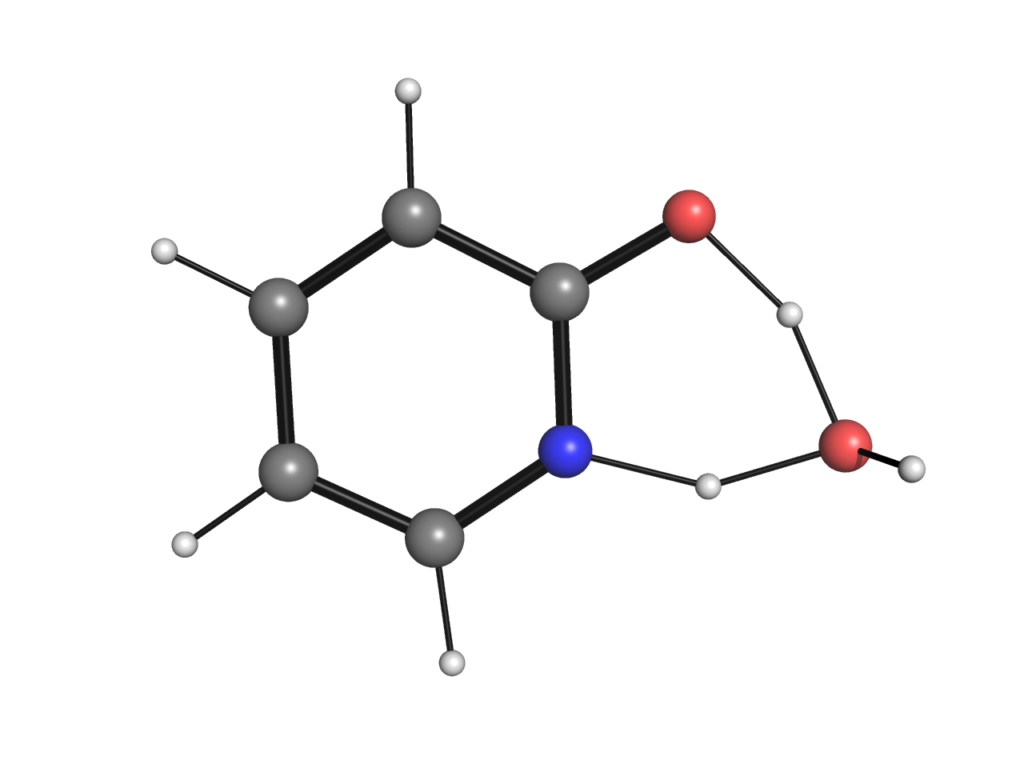
この場合水分子は単に酸素または窒素原子と水素結合を形成するのみならず,プロトンシャトルとして酸素と窒素原子の間の水素の受け渡しをしており,反応機構に直接関与しています.今回はこの例のように溶媒分子がポテンシャルエネルギー曲面の形を大きく変えるケースについて,溶媒分子をあらわにして量子化学計算を行っていくことで考察していきます.
psi4で溶媒をあらわに表現して量子化学計算
今回は再び2-ピリドンから2-ヒドロキシピリジンへの互変異性を題材に,水分子を追加して構造最適化を行っていきます.
- 水分子を追加して遷移状態の最適化
- 得られた遷移状態と原系,生成系の各構造に対して高精度のエネルギー計算を行い,PCM(IEFPCM)で水中での溶媒効果を見積もる
- 以前求めた水分子を介さない遷移状態と活性化エネルギーの比較を行う
という流れで行ってきます.
計算は「.py」をコマンドラインから実施することで行い,以下の環境で実施しました.手許の環境で試してみる場合は適宜設定ファイルを変更して下さい.
import sys
import pathlib
import numpy as np
import psi4
print(f'python version:\n{sys.version}')
# python version:
# 3.9.7 (default, Sep 16 2021, 13:09:58)
# [GCC 7.5.0]
print(f'numpy version:\t{np.__version__}')
# numpy version: 1.21.2
print(f'psi4 version:\t{psi4.__version__}')
# psi4 version: 1.5
filename = pathlib.Path(__file__)
logfile = filename.with_suffix('.log').name
psi4.set_output_file(logfile)
psi4.set_memory('12GB')
psi4.set_num_threads(12)
遷移状態の最適化
psi4.optimize(level-of-theory, molecule)
psi4.frequency(level-of-theory, molecule)
遷移状態の構造最適化はopt_typeオプションでtsを設定して行います.また正確なHessianを使って最適化した方が成功率が上がりますので,full_hess_everyオプションも設定しておいた方が無難です(0は計算開始時にHessianを計算).最適化が終わったら,同じ計算レベルで振動数計算を行い,虚振動が1つのみであることを確認します.今回はwB97X-D/6-31G(d)レベルにて構造最適化と振動数計算を行います.
なお以下のコードでは遷移状態に近い初期構造からはじめていますが,遷移状態の推定構造(初期構造)の探索には「psi4で遷移状態最適化:計算化学における虚振動と化学構造」という記事で紹介したようにある軸に沿ってエネルギーをスキャンしていくのが常法です.
level = 'wb97x-d/6-31G(d)'
mol: psi4.core.Molecule = psi4.geometry('''
0 1
C -1.073986885437 -1.170578359942 0.000002755738
C 0.953021017198 0.140745143377 -0.000003061297
C 0.196029366481 1.360797354321 -0.000001202096
C -1.155622586106 1.236381947214 0.000002880952
C -1.818434996700 -0.031125507024 0.000005467599
H -1.510894241728 -2.166796480067 0.000004269828
H 0.691726656323 2.319296967258 -0.000002742435
H -1.770734621411 2.131633416218 0.000004678262
H -2.895472126141 -0.076640107909 0.000009377672
O 2.177846935050 -0.264655641303 -0.000003962413
H 1.432324292904 -1.412270186206 -0.000002894660
N 0.288380859812 -1.071403950594 -0.000002249524
''')
print(f'optimizing TS w/ water ...')
psi4.set_options({'opt_type': 'ts',
'full_hess_every': 0,
'geom_maxiter': 300})
_, wfn = psi4.optimize(level,
molecule=mol,
return_wfn=True)
print(f'calculating frequencies ...')
_, wfn = psi4.frequency(level,
molecule=mol,
ref_gradient=wfn.gradient(),
return_wfn=True)
print(f'optimized structure:\n{mol.save_string_xyz()}')
freqs = np.array(wfn.frequencies())
print(f'frequencies:\n{freqs}')
得られた構造と振動数は以下の通りです.無事に唯一の負の振動数「-1693」が得られました.
optimized structure: 0 1 C -2.059804939004 -0.883939515300 0.016896641594 C -2.142670896585 0.522601087867 0.034373401662 C -1.005327856892 1.292137964650 0.025819124801 C 0.262128691322 0.655780273599 0.000149989930 C -0.809296733651 -1.450233360684 -0.006977337441 H -2.947090445439 -1.504862009531 0.020116162769 H -3.116351053856 1.004058321974 0.053181708105 H -1.034287493258 2.374975753357 0.035605898574 H -0.659869391828 -2.525258880890 -0.023896123570 N 0.310925009160 -0.705786602154 -0.011754036656 O 1.373676571106 1.306595996626 -0.012556673040 H 2.241663568347 0.464742550392 -0.051033211027 H 1.539325665427 -1.010395904629 -0.033586558790 O 2.724571979738 -0.663301399386 -0.078932817322 H 3.137792164668 -0.829819474500 0.778335970279 frequencies: [-1693.97050959 108.52469341 219.32166018 336.01629293 414.29659904 479.68588692 526.97669219 573.4584824 586.26145134 622.34668986 655.85304778 721.44694175 761.70436972 804.04705622 882.40448202 884.0240322 980.91665952 1010.00057372 1015.9519997 1068.92731766
虚振動に対応する振動モードを可視化したものが次の動画になります.水がプロトンシャトルとして働いている様子が見え,望みの遷移状態が求められたと判断できます.
PCMモデルによる溶媒効果の評価
psi4.pcm_helper(pcm-input)
続いて真空中のwB97X-D/6-31G(d)レベルでの最適化構造に対して,PCM Solverを用いて溶媒効果を見積もります.具体的には今回はIEFPCM(Water)を用い,wB97X-D/6-311++G(2d,p)レベルでのエネルギー計算を行ってみます.
psi4でPCM Solverを利用するにはpcmオプションをTrueにし,pcm_helperを用いて上記のフォーマットに従って作成したPCM Solverのインプットファイルを読み込みます.
level = 'wb97x-d/6-311++G(2d,p)'
pcm = '''
units = angstrom
medium
{
solvertype = iefpcm
solvent = Water
}
cavity
{
type = gepol
scaling = True
radiiset = uff
mode = implicit
}
'''
ts_water = psi4.geometry('''
0 1
C -2.059804939004 -0.883939515300 0.016896641594
C -2.142670896585 0.522601087867 0.034373401662
C -1.005327856892 1.292137964650 0.025819124801
C 0.262128691322 0.655780273599 0.000149989930
C -0.809296733651 -1.450233360684 -0.006977337441
H -2.947090445439 -1.504862009531 0.020116162769
H -3.116351053856 1.004058321974 0.053181708105
H -1.034287493258 2.374975753357 0.035605898574
H -0.659869391828 -2.525258880890 -0.023896123570
N 0.310925009160 -0.705786602154 -0.011754036656
O 1.373676571106 1.306595996626 -0.012556673040
H 2.241663568347 0.464742550392 -0.051033211027
H 1.539325665427 -1.010395904629 -0.033586558790
O 2.724571979738 -0.663301399386 -0.078932817322
H 3.137792164668 -0.829819474500 0.778335970279
''')
psi4.set_options({'pcm': True})
psi4.pcm_helper(pcm)
print(f'calc energy of TS w/ explicit water molecule ...')
e = psi4.energy(level,
molecule=ts_water)
print(f'calcd energy: {e}')
反応エネルギーの考察
ここまで,水分子をあらわにした遷移状態のwB97X-D/6-31G(d)レベルでの構造最適化と,PCM Solverを用いたIEFPCM(Water)/wB97X-D/6-311++G(2d,p)レベルでのエネルギー計算を行ってきました.同様にして,
- 2-ピリドン
- 2-ヒドロキシピリジン
- 水
- 4員環遷移状態
- 2-ピリドンと水
- 2-ヒドロキシピリジンと水
のそれぞれの構造に関しても同じ計算レベルで構造最適化とエネルギー計算を行います.
各々について,構造最適化と同じレベルで行った振動数計算から得られた自由エネルギー補正項を取得し,高精度で計算したエネルギーに足していきます.私の環境では以下の値が得られました.エネルギーの単位はhartreeです.
| 化合物 | 電子エネルギー | 補正項 | 自由エネルギー |
|---|---|---|---|
| 2-ピリドン | -323.51557 | 0.06627825 | -323.4493 |
| 2-ヒドロキシピリジン | -323.50904 | 0.06615921 | -323.44288 |
| 水 | -76.439359 | 0.00401739 | -76.435341 |
| 4員環遷移状態 | -323.45055 | 0.06115941 | -323.38939 |
| 2-ピリドンと水 | -399.96153 | 0.08392389 | -399.85622 |
| 2-ヒドロキシピリジンと水 | -399.96153 | 0.08876168 | -399.87277 |
| 6員環遷移状態 | -399.94014 | 0.08392389 | -399.85622 |
得られた値をもとに作成したエネルギー図が以下になります(縦軸の絶対値は適当です).黒線が4員環遷移状態,青線が6員環遷移状態の機構を示しています.

この図から以下のことがわかります.
- 2−ピリドンの方が安定
- 水を介する6員環遷移状態の方が20 kcal/mol程活性化エネルギーが低い
- 基質と水が相互作用した構造はこの計算レベルだと不利
特に最後の項目がわかりにくいかもしれません.これはPCMモデルの時点で,ピリジン窒素やフェノール性水酸基への水の配位で得られる溶媒和のエネルギーある程度評価できていることを意味していると考えられます.実際,真空中で計算すると水と相互作用した方が4 kcal/mol程度安定と見積もられます.
今回は計算対象として,「孤立した」2−ピリドンの互変異性を考えてきました.実験的には固体中,及び極性溶媒中では今回の計算で示されたように2−ピリドンの方が安定,非極性溶媒中では逆に2−ヒドロキシピリジンの方が安定と知られています.異性化のメカニズムですが,今回のようなプロトン性溶媒が関与するものの他にも,2−ピリドンと2−ヒドロキシピリジンからなる二量体から進行するものなどいくつか提唱されており,実際にはこれら複数の機構の総和を観測していると考えられています.
終わりに
今回は「psi4で溶媒の直接関与を考慮する」という話題について,
- 連続誘電体モデルでは扱えない溶媒効果
- 2-ピリドンの互変異性を例にpsi4を用いた計算
について触れてきました.水分子をあらわにして計算することで,活性化エネルギーの低い遷移状態を見出すことができました.この方法でモデル化できる溶媒分子の数はせいぜい4,5分子までです.少ないように思えるかもしれませんが,溶質に直接関与する溶媒分子はほぼこの数以内に収まると思われます.例えば水分子同士が水素結合を形成することで生じる効果など,もっと多くの溶媒分子を含む系をモデル化したい場合は,分子動力学法(Molecular Dynamics, MD)が選択肢になります.
これまで溶質と溶媒分子の相互作用を,静電力や分散力などに分けて考えてきました.一般にこのような非結合性相互作用における内訳を理解する手法をエネルギー分解法と呼びます.psi4ではエネルギー分解法の一つであるSAPTと呼ばれる手法が実装されています.次回はSAPTについて学んでいくことで,様々な非結合性相互作用の特徴を理解していきたいと思います.
コメント