NumPyのrandomモジュールを使うことで,様々な形の乱数を発生させることができます.このエントリーではnumpy.randomの基本的な使い方について記していきます.よく使う機能に絞って簡潔に説明していきますので,詳細はnumpy randomモジュールの公式ドキュメントを参照してください.
乱数発生に用いるnumpy.randomの主要なメソッド
まずは代表的なメソッドについて見ていきましょう.主に,
- シンプルに乱数を発生させる方法
- ある統計分布に従った形で乱数を発生させる方法
の2つの方法があります.それぞれについてテーブルにまとめておきます.
シンプルに乱数を発生させる方法
小数,整数,配列からのランダムサンプリングなどの方法が揃っています.
| メソッド | 説明 |
|---|---|
| random.rand() | 0以上1未満の小数を返す.rand(n)とすればn個配列で,rand(m,n)とすればnumpy配列で返す |
| random.randint(m,n,x) | m以上n未満の整数をx個返す.xを(a,b)とすれば配列で帰ってくる |
| random.choice() | 与えられた集合からランダムにサンプリング |
| random.shuffle() | 与えられた配列の順番をランダムに並べ替える |
統計分布に従った乱数を発生させる方法
(標準)正規分布,二項分布,ポワソン分布,χ二乗分布などからのサンプリングが可能です.
| メソッド | 説明 |
|---|---|
| random.randn() | 平均0,標準偏差1の正規分布からのサンプリング |
| random.normal(loc=x, scale=y, size=z) | 平均x,標準偏差yの正規分布からのサンプリング |
| random.binominal() | 二項分布からのサンプリング |
| random.poisson(lam=x) | ポワソン分布からのサンプリング |
| random.chisquare(df) | χ二乗分布からのサンプリング |
pythonのコードで乱数発生の具体例を解説
準備
まずは必要なライブラリのimportを行いましょう.
import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set()
ランダムに数字を取得
0以上1未満の小数を指定された大きさで返します.
# 0以上1未満[0,1)のランダムな数字を5個 np.random.rand(5) # 3x2のnumpy配列で返す np.random.rand(3,2)
ランダムに整数を取得
ランダムな整数の値を取得します.引数が1つの場合は0以上引数以下の整数を1つ,2つの場合は引数を範囲とした乱数を発生させます.
# [5,10)のランダムな整数を10個 np.random.randint(5, 10, size=10) # [0,5)のランダムな整数を2x4のnumpy配列で返す np.random.randint(5, size=(2,4))
配列からのランダム抽出
与えられた配列からのランダム抽出を行います.replaceオプションによって復元抽出(デフォルト),及び非復元抽出の設定が可能です.配列中の各要素の生起確率をオプションpを与えることで設定可能です.
下記のコードでは出現確率がp(1)=0.5, p(3)=0.25, p(5)=0.25である配列[1,3,5]から10回の復元抽出を行っています.
np.random.choice([1,3,5], size=10, replace=False, p=[0.5, 0.25, 0.25])
配列をランダムにシャッフル
このメソッドは与えられた配列の順番をランダムにシャッフルして返します.元の配列が置き換えられることに注意してください.このメソッドは例えば機械学習のデータをランダムに並べ替えて,学習用セットとテストセットに分ける場合などに使えます.
x = [1,10,100,1000,10000] np.random.shuffle(x) x # [10, 100, 10000, 1000, 1]
標準正規分布からの乱数発生
平均0,標準偏差1の標準正規分布からのサンプリングを行います.確率密度関数は次式で表されます.
$$ P(X)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})$$
np.random.randn(2,4) # 2x4の配列で返す
正規分布からの乱数発生
平均loc,標準偏差scaleの正規分布からサンプルを取得します.確率密度関数は平均μ,標準偏差σとして次式で表されます.
$$P(X) = \frac{1}{\sqrt{2 \pi \sigma ^2}}\exp(-\frac{(x-\mu)^2}{2\sigma ^2})$$
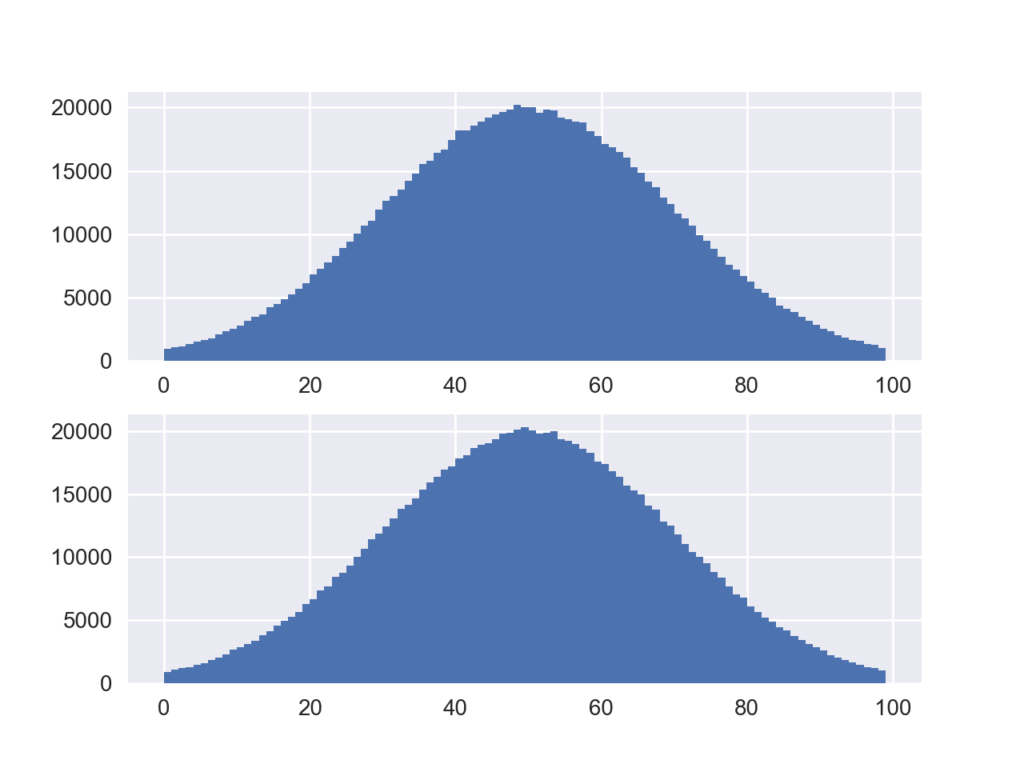
下のコードでは平均50,標準偏差20の正規分布から100万個サンプルしたものをx1,標準正規分布を平均50,標準偏差20の正規分布に変換して100万個サンプルしたものをx2として,2つのヒストグラムを描いています.
x1 = np.random.normal(loc=50, scale=20, size=1000000) x2 = 20 * np.random.randn(1000000) + 50 # ヒストグラムを描いて2つを比較 fig = plt.figure() bins=range(0,100) ax1 = fig.add_subplot(211) ax1.hist(x1, bins=bins) ax2 = fig.add_subplot(212) ax2.hist(x2, bins=bins)
当然ですが下の通りほぼ同じ分布が得られています.因みに実行速度はrandintを用いた方がかなり速いようです.
二項分布からの乱数発生
生起確率pの事象をn回繰り返す試行をsize回数行います.二項分布の確率質量関数は次式で表されます.
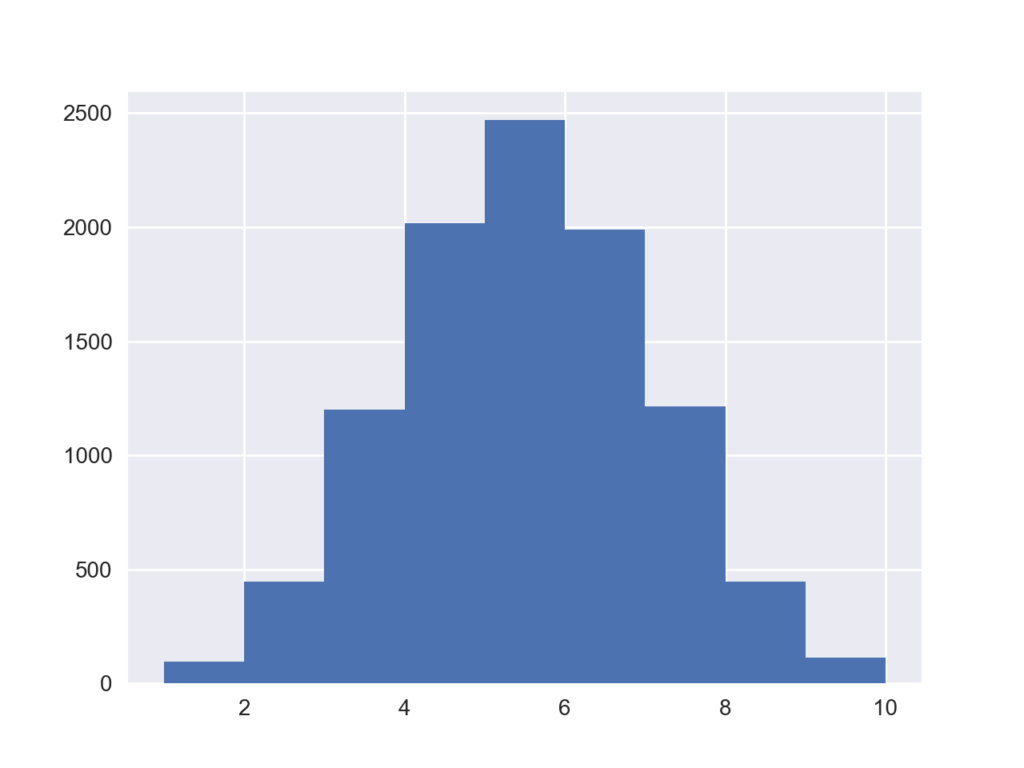
下のコードでは表裏が等確率で出るコインを10回投げて表が出た回数を数える試行を10000回繰り返した結果をヒストグラムで示したものです.
x = np.random.binominal(10,0.5,10000) plt.hist(x, bins=range(1,11))
ポワソン分布からの乱数発生
ポワソン分布は滅多に起きない事象について用いられる特殊な二項分布です.1つの変数λによって分布の形が変化し,その平均及び分散がともにλになるという特徴があります.その確率質量関数は次式で表されます.
$$f(k) = \frac{\lambda^k\exp(-\lambda)}{k!}$$
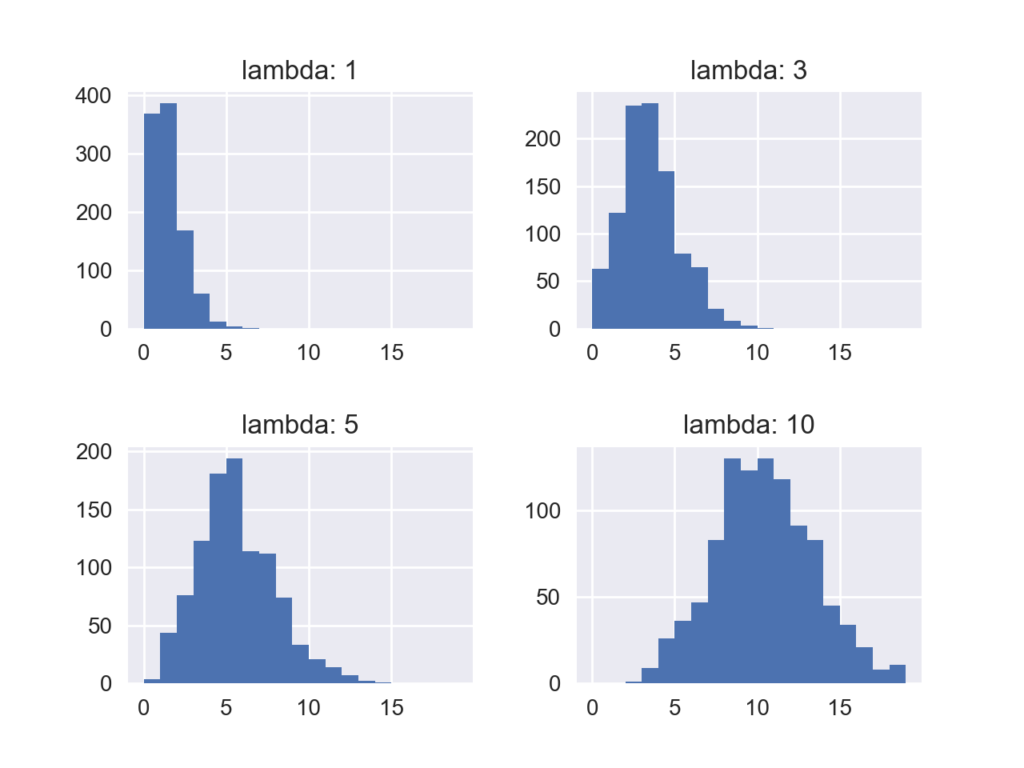
下のコードは異なるλを用いてそれぞれ1000回ずつサンプリングを行った結果をヒストグラムで示したものです.
lambdas = [1,3,5,10]
i = [221,222,223,224]
fig = plt.figure()
plt.subplots_adjust(hspace=0.5, wspace=0.3)
for l,m in zip(lambdas,i):
x = np.random.poisson(lam=l, size=1000)
ax = fig.add_subplot(m)
ax.hist(x, bins=range(20))
ax.set_title('lambda: {}'.format(l))
χ二乗分布からの乱数発生
自由度dfに従うχ二乗分布からのサンプリングを行います.下のコードでは異なる自由度dfを用いてそれぞれ1000回ずつサンプリングを行った結果をヒストグラムで示したものです.
dfs = [1,3,5,10]
i = [221,222,223,224]
fig = plt.figure()
plt.subplots_adjust(hspace=0.5, wspace=0.3)
for d,m in zip(dfs,i):
x = np.random.chisquare(df=d, size=1000)
ax = fig.add_subplot(m)
ax.hist(x, bins=range(20))
ax.set_title('df: {}'.format(d))

終わりに
今回はnumpyのランダムモジュールを用いて乱数の発生方法や,様々な統計分布からのサンプリング方法について学んできました.次回はscipyライブラリの統計モジュールを用いることで,さらに統計分布について理解を深めていきたいと思います.
>>次の記事:「Scipyの統計モジュールstatsで統計分布を使いこなす」
コメント